كيفية إجراء اختبار فيشر الدقيق في spss
يتم استخدام اختبار فيشر الدقيق لتحديد ما إذا كان هناك ارتباط كبير بين متغيرين فئويين أم لا.
يتم استخدامه عمومًا كبديل لاختبار مربع كاي للاستقلال عندما يكون عدد الخلايا الواحدة أو أكثر في جدول 2 × 2 أقل من 5.
يشرح هذا البرنامج التعليمي كيفية إجراء اختبار فيشر الدقيق في برنامج SPSS.
مثال: اختبار فيشر الدقيق في SPSS
لنفترض أننا نريد أن نعرف ما إذا كان الجنس مرتبطًا بتفضيل حزب سياسي في كلية معينة أم لا. لاستكشاف ذلك، قمنا بإجراء مسح عشوائي لـ 25 طالبًا في الحرم الجامعي. ويبين الجدول أدناه عدد الطلاب الديمقراطيين أو الجمهوريين حسب جنسهم:
| ديمقراطي | جمهوري | |
|---|---|---|
| أنثى | 8 | 4 |
| ذكر | 4 | 9 |
لتحديد ما إذا كان هناك ارتباط ذو دلالة إحصائية بين الجنس وتفضيل الحزب السياسي، يمكننا استخدام الخطوات التالية لإجراء اختبار فيشر الدقيق في SPSS:
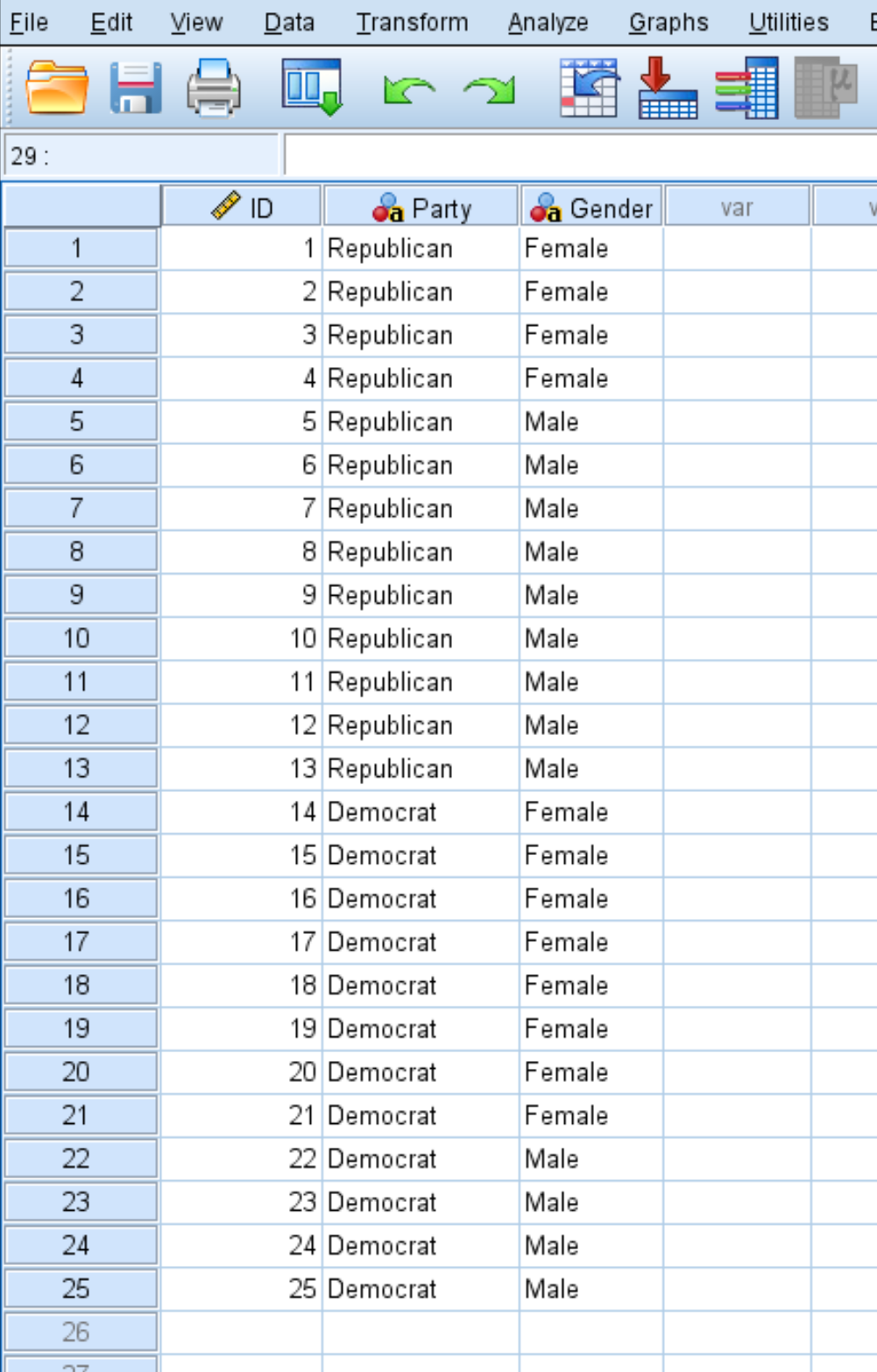
الخطوة 1: أدخل البيانات.
أولا قم بإدخال البيانات كما هو موضح أدناه:
يعرض كل صف هوية الفرد وتفضيلات الحزب السياسي والجنس.
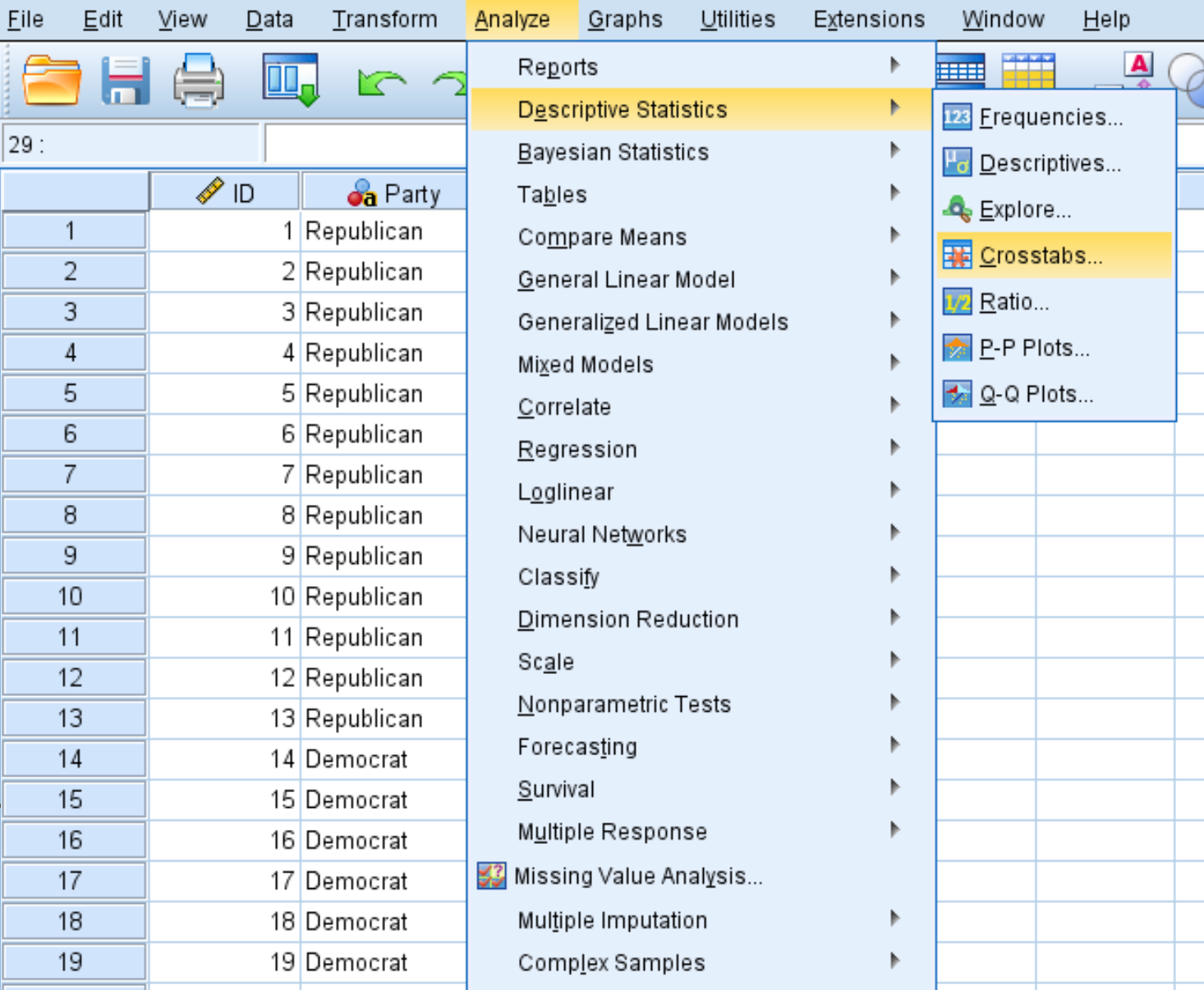
الخطوة 2: إجراء اختبار فيشر الدقيق.
انقر فوق علامة التبويب تحليل ، ثم الإحصائيات الوصفية ، ثم الجداول الترافقية :
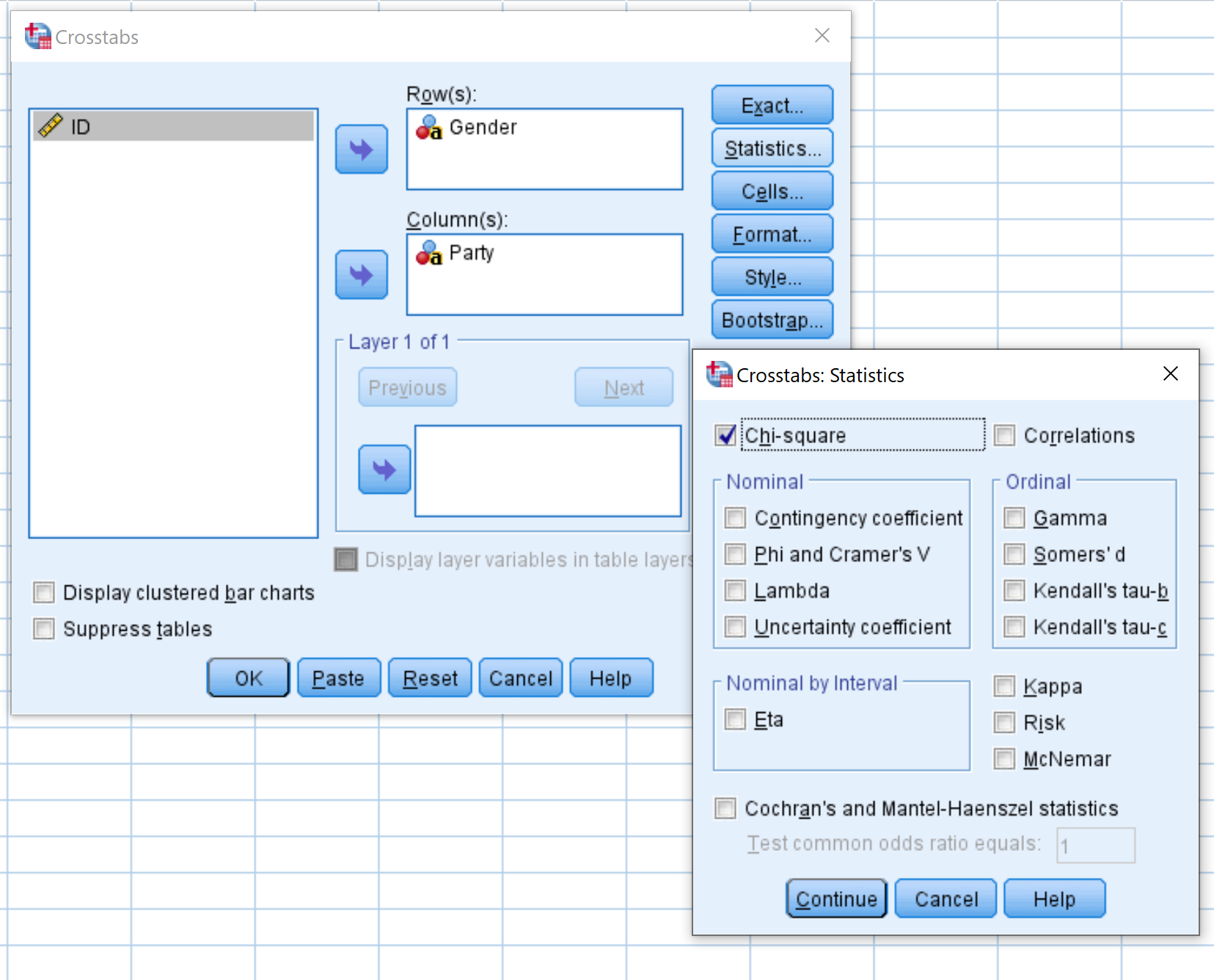
اسحب متغير الجنس إلى المنطقة المسماة “الصفوف” ومتغير الجزء إلى المنطقة المسماة “أعمدة”. ثم انقر فوق الزر المسمى “الإحصائيات” وتأكد من تحديد المربع المجاور لمربع الطاقة . ثم انقر فوق “متابعة” .
بعد ذلك، انقر فوق الزر المسمى Exact وتأكد من تحديد المربع الموجود بجوار Exact . ثم انقر فوق “متابعة” .
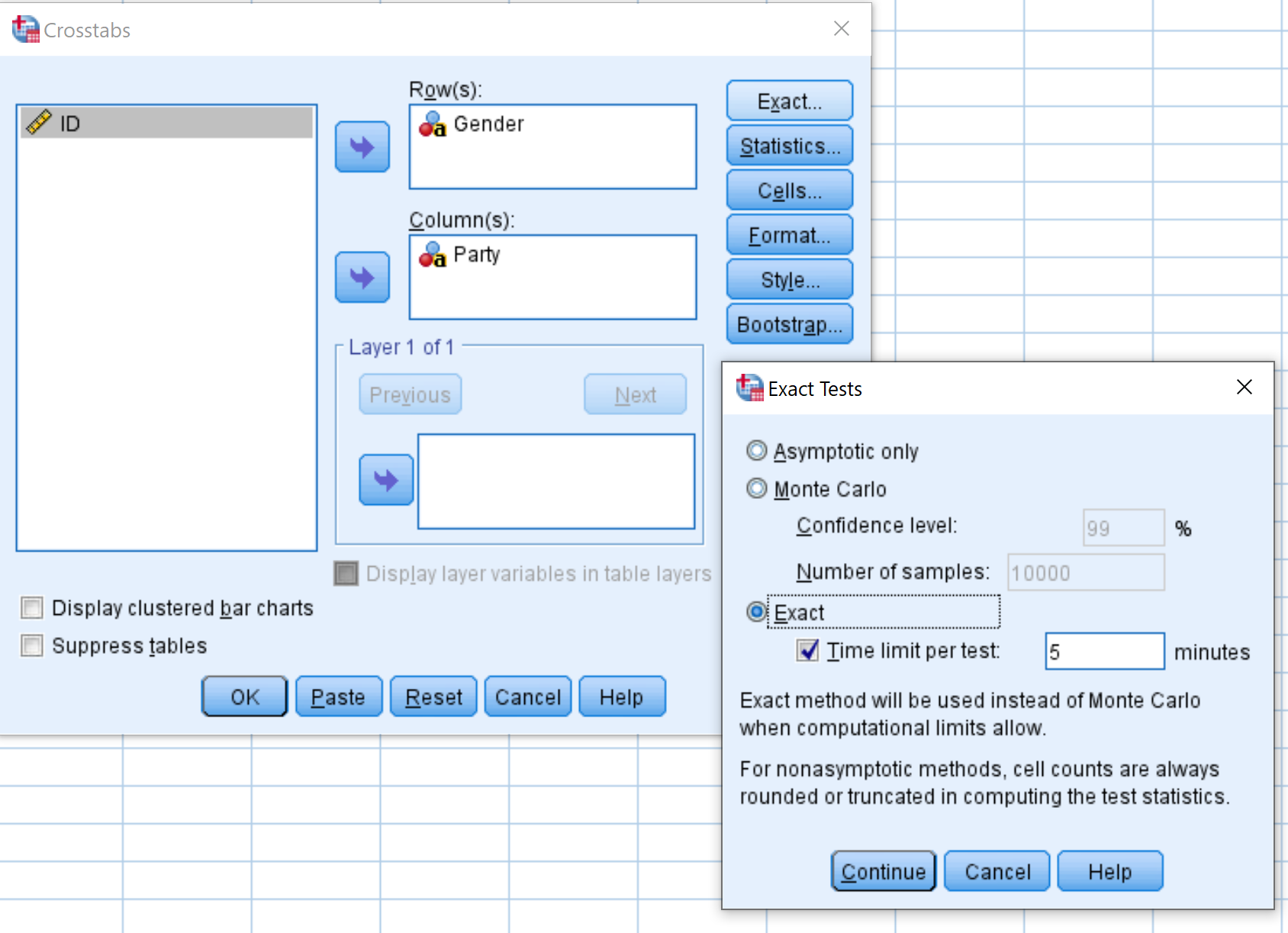
وأخيرًا، انقر فوق “موافق” لإجراء اختبار فيشر الدقيق.
الخطوة 3: تفسير النتائج.
بمجرد النقر فوق “موافق” ، سيتم عرض نتائج اختبار فيشر الدقيق:
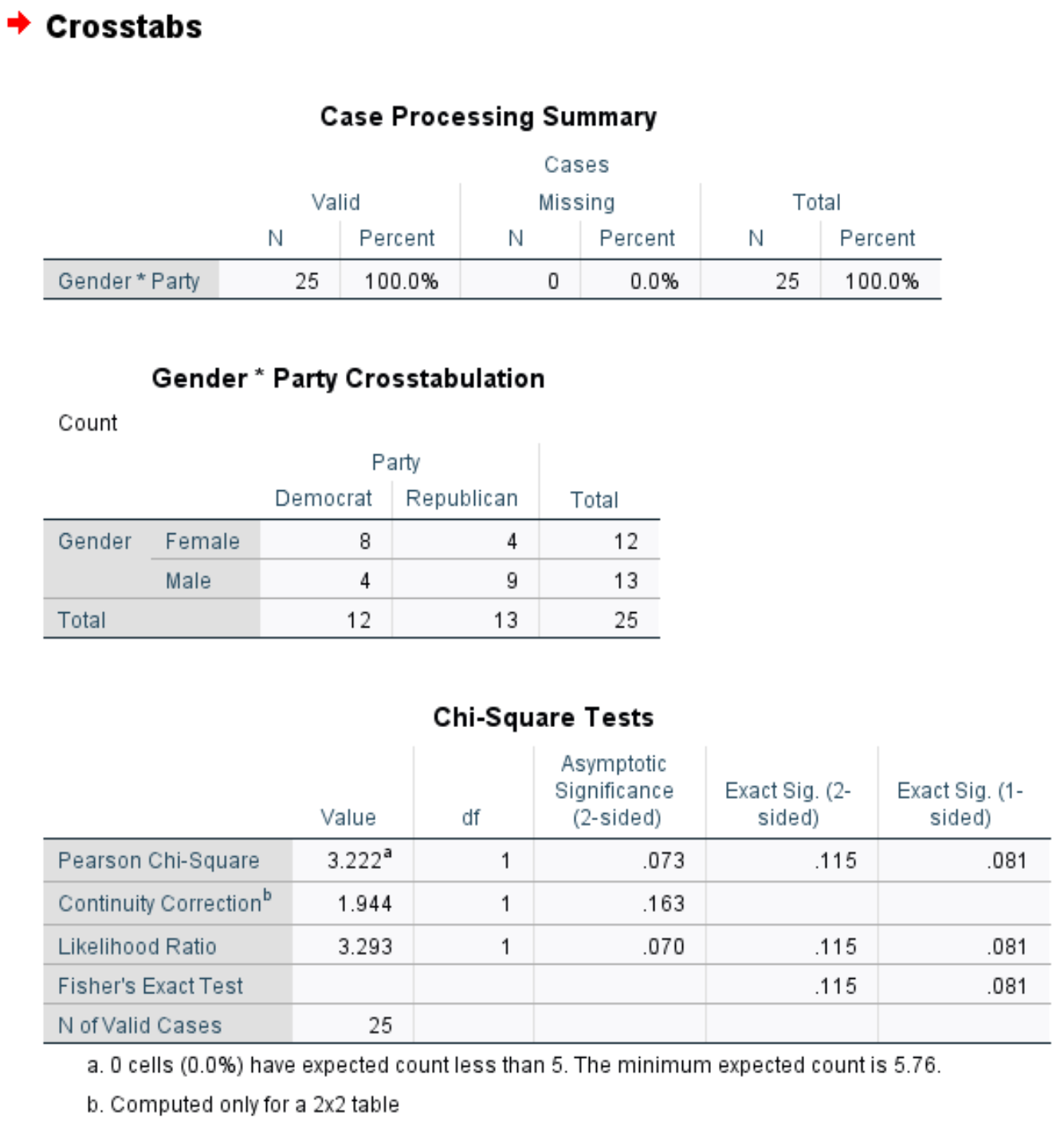
يعرض الجدول الأول عدد الحالات المفقودة في مجموعة البيانات. يمكننا أن نرى أن هناك 0 حالة مفقودة في هذا المثال.
ويعرض الجدول الثاني تبويباً متقاطعاً لإجمالي عدد الأفراد حسب الجنس وتفضيل الحزب السياسي.
ويبين الجدول الثالث نتائج اختبار فيشر الدقيق. يمكننا أن نرى القيمتين p التاليتين للاختبار:
- القيمة p على الوجهين: 0.115
- قيمة p من جانب واحد: 0.081
الفرضية الصفرية لاختبار فيشر الدقيق هي أن المتغيرين مستقلان. في هذه الحالة، فرضيتنا الصفرية هي أن الجنس وتفضيل الحزب السياسي مستقلان، وهو اختبار ذو طرفين، لذلك سنستخدم القيمة الاحتمالية ثنائية الطرف البالغة 0.115.
وبما أن هذه القيمة p لا تقل عن 0.05، فإننا لا نرفض فرضية العدم. ولذلك ليس لدينا أدلة كافية لنقول أن هناك علاقة ذات دلالة إحصائية بين الجنس وتفضيل الحزب السياسي.