كيفية إجراء اختبار t المقترن باليد

يتم استخدام اختبار t للعينات المقترنة لمقارنة متوسطي عينتين عندما يمكن ربط كل ملاحظة في عينة واحدة بملاحظة في العينة الأخرى.

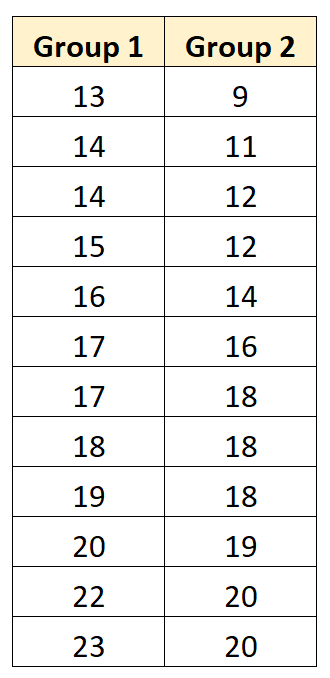
يوضح المثال التالي خطوة بخطوة كيفية إجراء اختبار t للعينات المقترنة لتحديد ما إذا كان متوسط عدد السكان متساويًا بين المجموعتين التاليتين:

الخطوة 1: حساب إحصائية الاختبار

يتم حساب إحصائية الاختبار لاختبار t المقترن على النحو التالي:

ر = س _فرق / (ق _فرق /√ ن )

ذهب:

• x _diff : مثال لمتوسط الاختلافات
• الصورة: مثال على الانحراف المعياري للاختلافات
• n: حجم العينة (أي عدد الأزواج)

وسوف نقوم بحساب متوسط الفروق بين المجموعتين والانحراف المعياري للفروق بين المجموعتين:

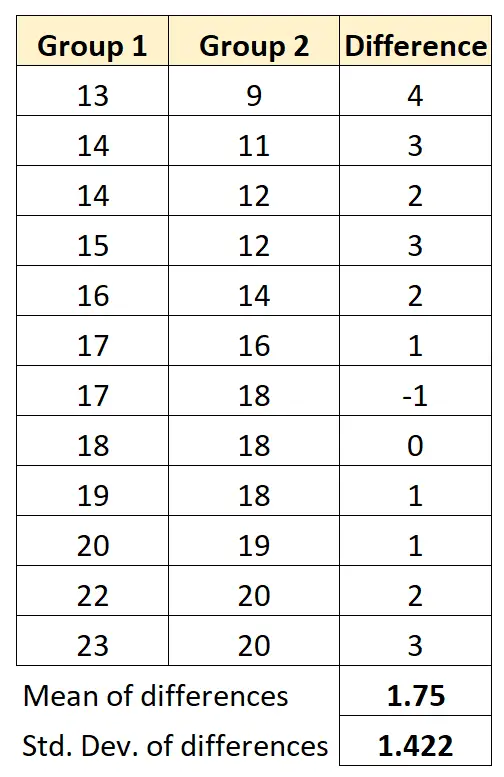
وبالتالي، يمكن حساب إحصائية الاختبار لدينا على النحو التالي:

• ر = س _فرق / (ق _فرق /√ ن )
• ر = 1.75 / (1.422/√ 12 )
• ر = 4.26

الخطوة 2: حساب القيمة الحرجة

بعد ذلك، علينا إيجاد القيمة الحرجة لمقارنة إحصائيات الاختبار لدينا.

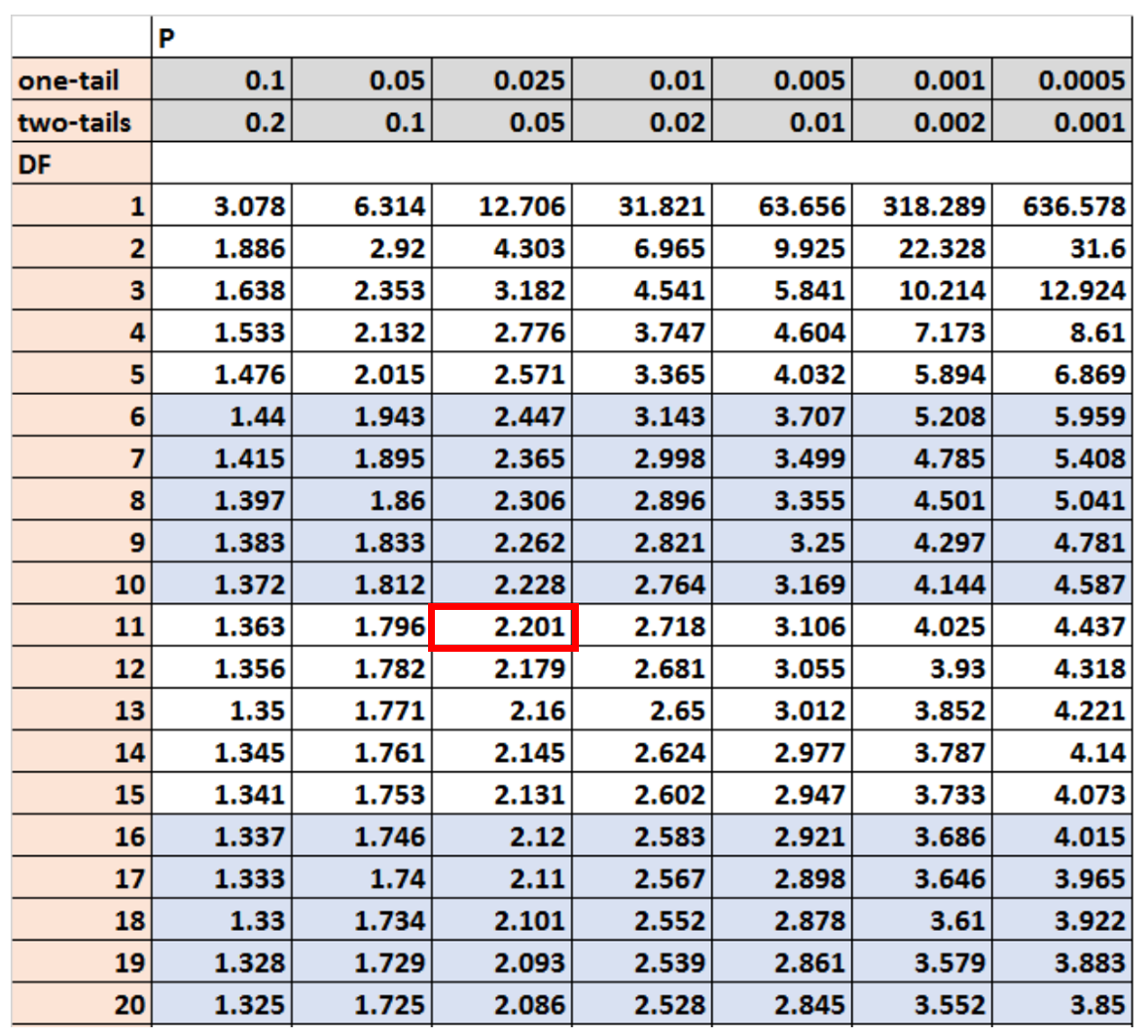
في هذا المثال، سوف نستخدم اختبارًا ثنائيًا بدرجات حرية α = 0.05 وdf = n-1.

ووفقا لجدول التوزيع t فإن القيمة الحرجة المقابلة لهذه القيم هي 2.201 :

الخطوة 3: رفض أو الفشل في رفض الفرضية الصفرية

يستخدم اختبار t للعينات المقترنة الفرضية الصفرية والبديلة التالية:

• H ₀ : μ ₁ = μ ₂ (متوسطا السكان متساويان)
• H _A : μ ₁ ≠ μ ₂ (وسطا السكان غير متساويين)

بما أن القيمة المطلقة لإحصائيات الاختبار ( 4.26 ) أكبر من القيمة الحرجة الموجودة في جدول t ( 2.201 )، فإننا نرفض فرضية العدم.

وهذا يعني أن لدينا ما يكفي من الأدلة لنقول أن المتوسط بين المجموعتين ليس متساويا.

المكافأة: لا تتردد في استخدام حاسبة اختبار t للعينات المقترنة لتأكيد نتائجك.