كيفية إجراء اختبار t لعينتين في برنامج spss
يتم استخدام اختبار t المكون من عينتين لاختبار ما إذا كانت متوسطات مجتمعين متساويتين أم لا.
يشرح هذا البرنامج التعليمي كيفية إجراء اختبار t المكون من عينتين في برنامج SPSS.
مثال: اختبار t لعينتين في برنامج SPSS
يريد الباحثون معرفة ما إذا كانت المعالجة الجديدة للوقود تتسبب في تغيير متوسط عدد الكيلومترات المقطوعة لكل جالون في سيارة معينة. ولاختبار ذلك، أجروا تجربة حيث تلقت 12 سيارة معالجة الوقود الجديدة و12 سيارة لم تحصل عليها.
توضح لقطة الشاشة التالية ميلا في الغالون لكل سيارة مع المجموعة التي تنتمي إليها (0 = لا يوجد معالجة للوقود، 1 = معالجة الوقود):
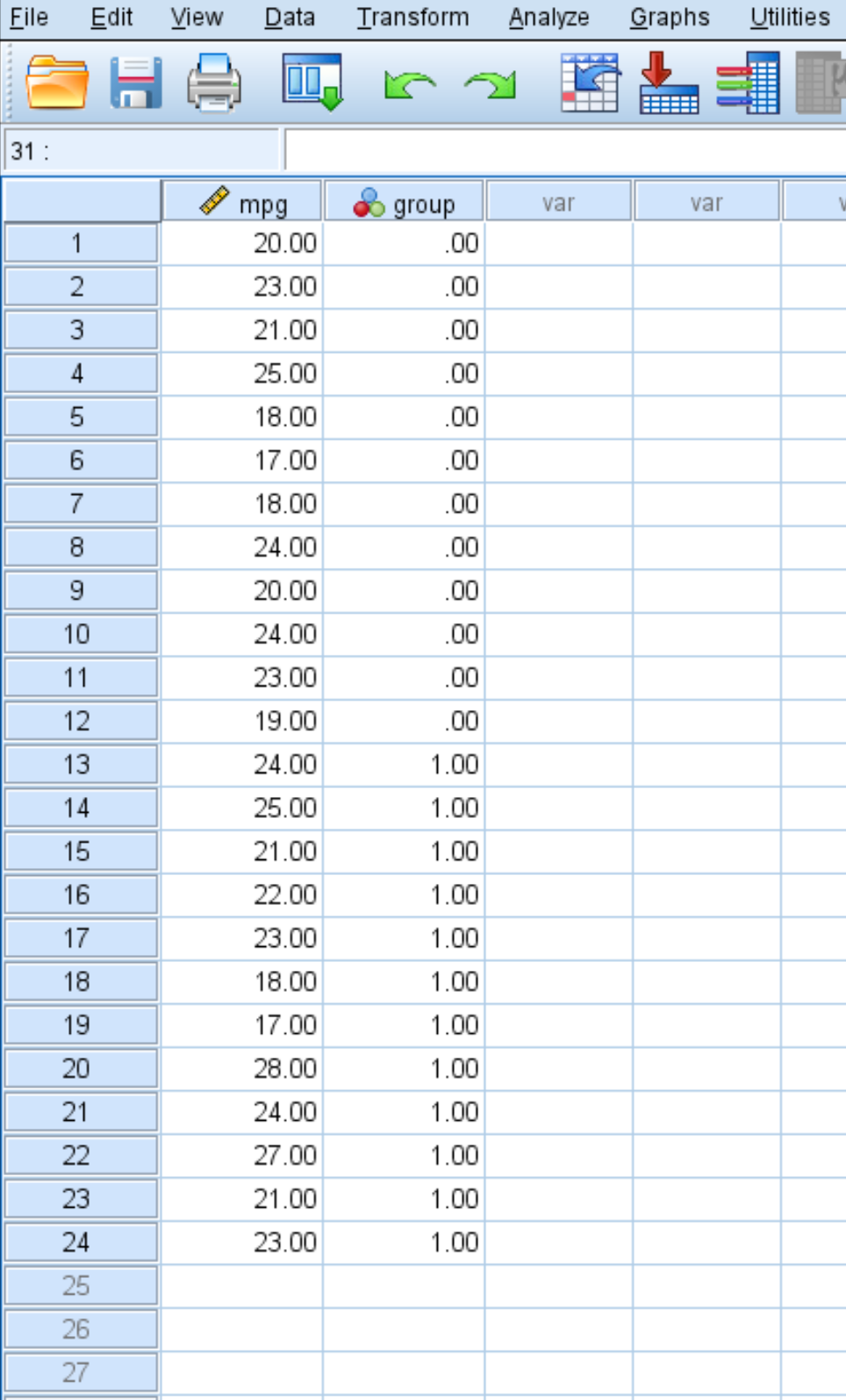
استخدم الخطوات التالية لإجراء اختبار t من عينتين لتحديد ما إذا كان هناك اختلاف في متوسط ميل لكل جالون بين هاتين المجموعتين، استنادًا إلى الفرضيات الخالية والبديلة التالية:
- H 0 : μ 1 = μ 2 (متوسط ميل لكل جالون بين المجموعتين متساوي)
- H 1 : μ 1 ≠ μ 2 (متوسط ميل لكل جالون بين المجموعتين غير متساوي)
استخدم مستوى أهمية α = 0.05.
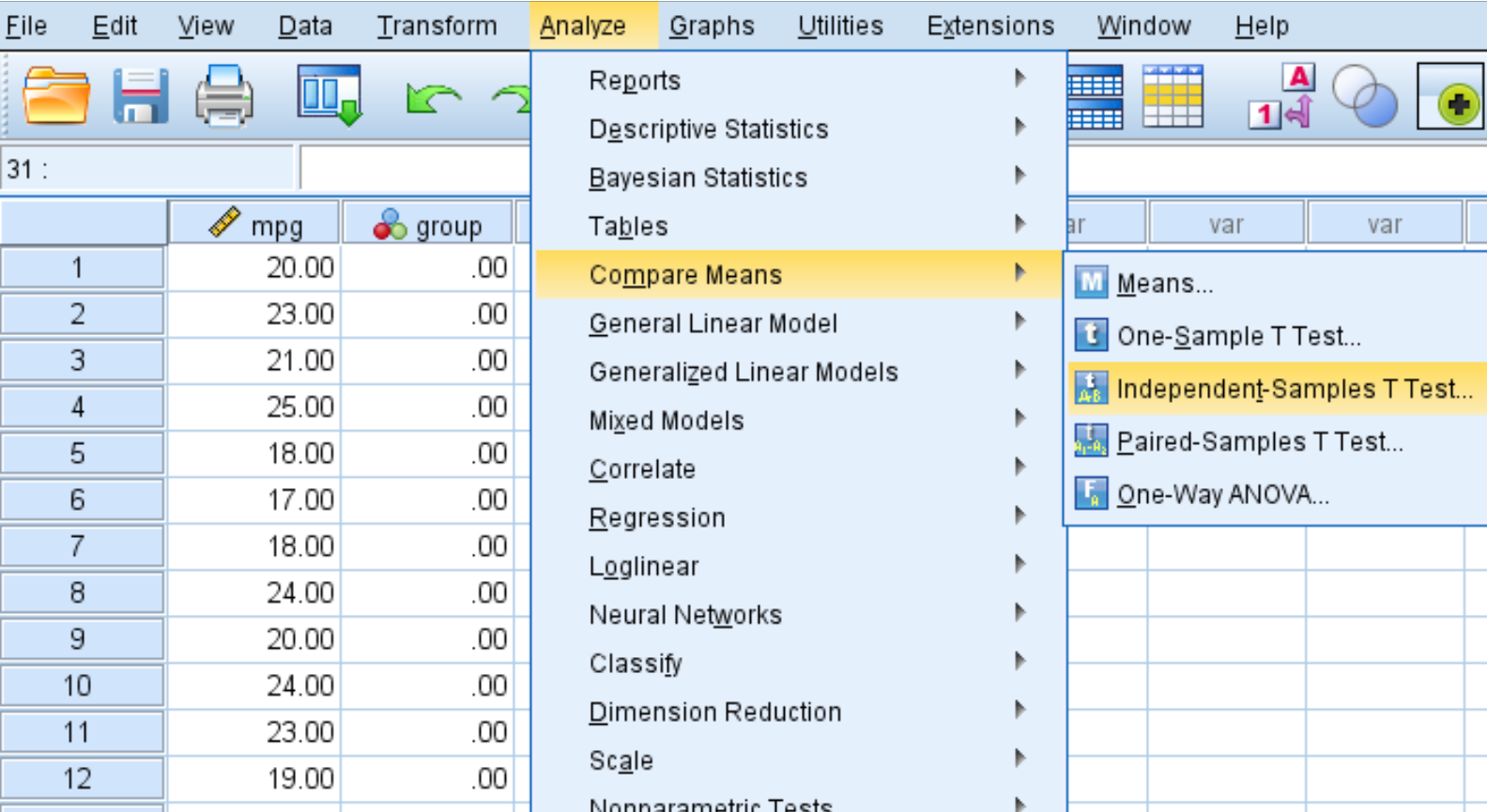
الخطوة 1: اختر خيار اختبار العينات المستقلة.
انقر فوق علامة التبويب تحليل ، ثم مقارنة الوسائل ، ثم اختبار T للعينات المستقلة :
الخطوة 2: املأ القيم اللازمة لإجراء اختبار t المكون من عينتين.
بمجرد الضغط على اختبار Independent-Samples T ، ستظهر النافذة التالية:
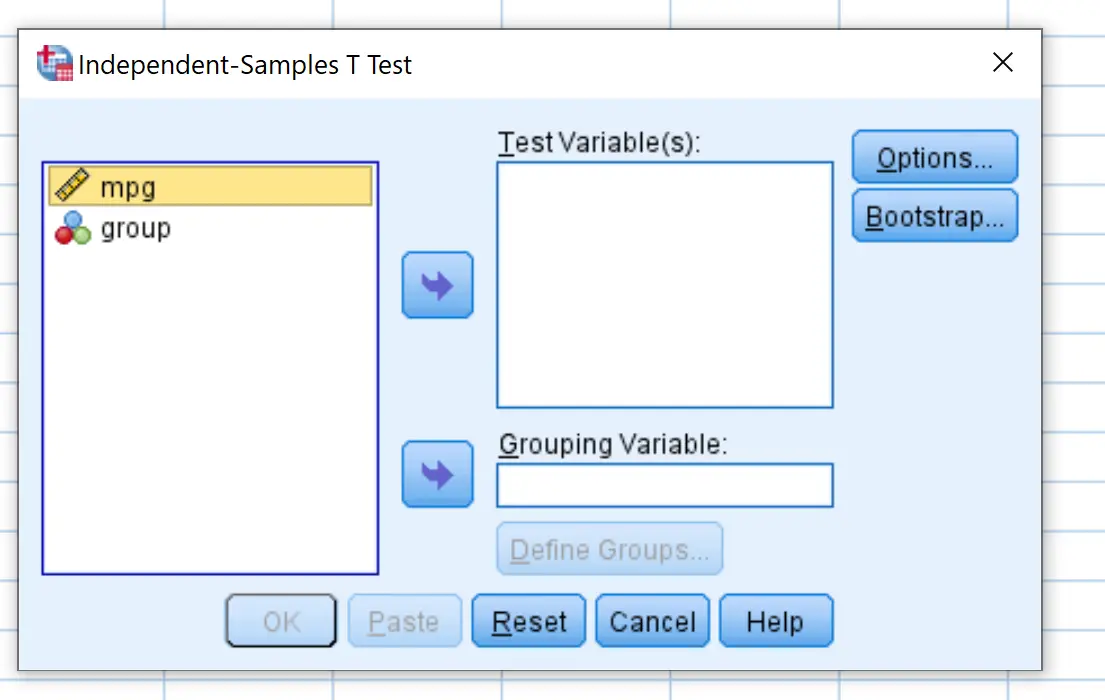
اسحب ميلا في الغالون إلى المربع المسمى اختبار المتغير (المتغيرات) وقم بتجميعه في المربع المسمى متغير التجميع . ثم انقر فوق تحديد المجموعات وحدد المجموعة 1 كالصفوف ذات القيمة 0 وحدد المجموعة 2 كالصفوف ذات القيمة 1. ثم انقر فوق موافق .
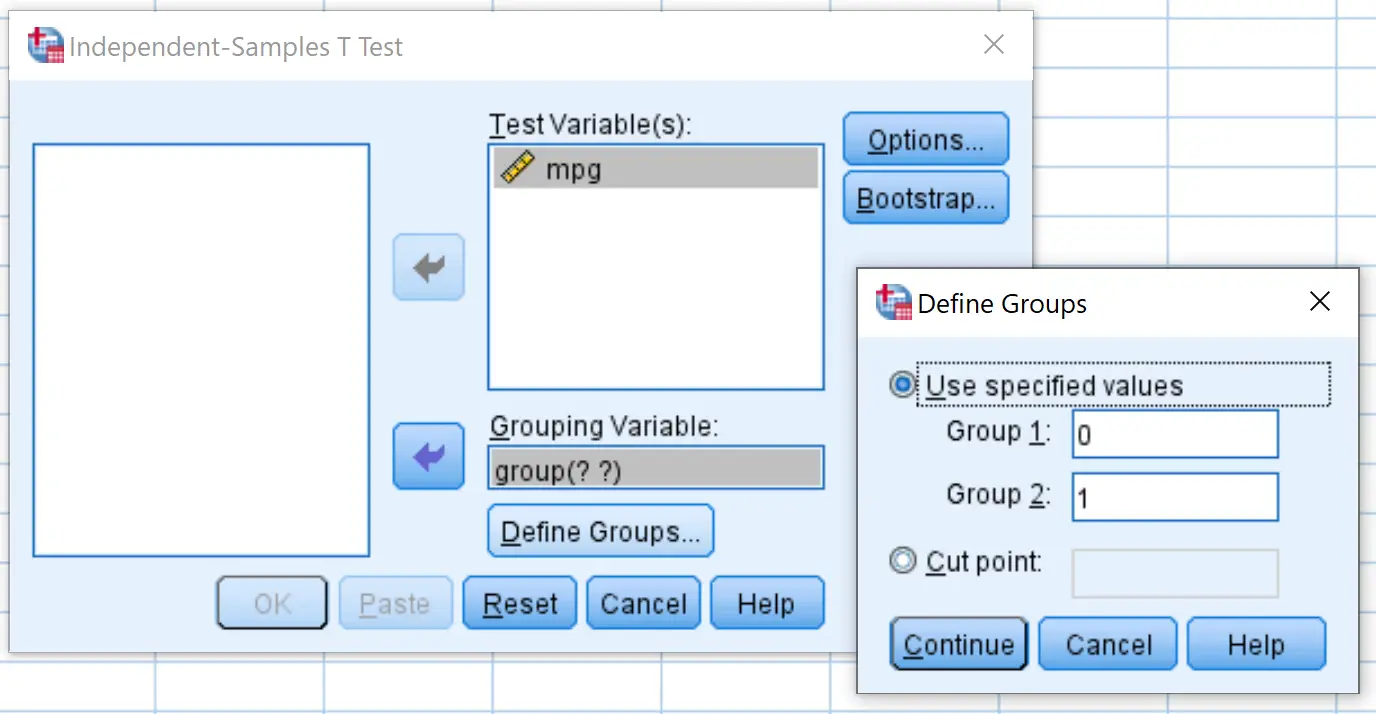
الخطوة 3: تفسير النتائج.
بمجرد النقر فوق “موافق” ، سيتم عرض نتائج اختباري t النموذجيين:
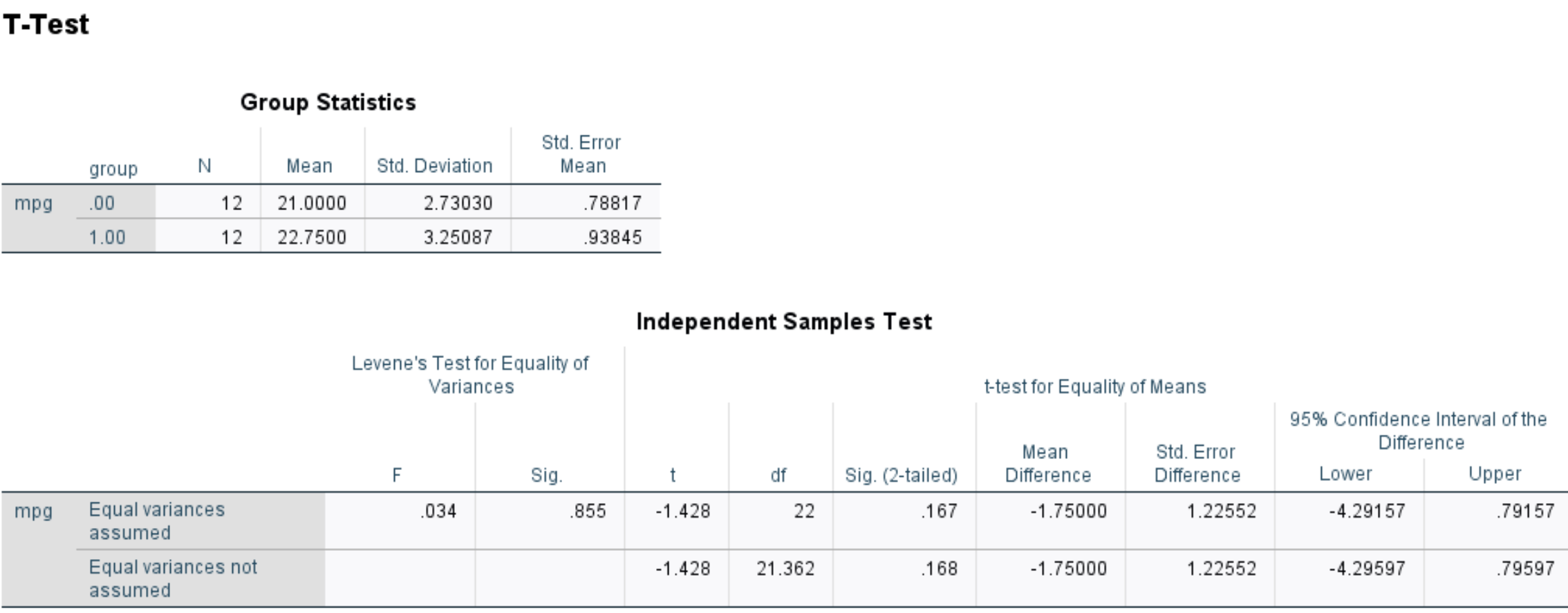
يعرض الجدول الأول الإحصائيات الموجزة التالية للمجموعتين:
- ن: حجم العينة
- المتوسط: متوسط عدد الأميال لكل جالون من السيارات في كل مجموعة
- معيار. الانحراف: الانحراف المعياري للميل لكل جالون من السيارات في كل مجموعة
- معيار. يعني الخطأ: الخطأ المعياري لمتوسط ميلا في الغالون، محسوبة في s/√n
ويعرض الجدول الثاني نتائج اختبار t للعينتين. يعرض الصف الأول نتائج الاختبار إذا افترضت أن التباين بين المجموعتين متساوي. يعرض السطر الثاني نتائج الاختبار إذا لم تقم بهذا الافتراض.
في هذه الحالة، ينتج كلا الإصدارين من الاختبار نتائج متطابقة تقريبًا. لذا سنشير ببساطة إلى نتائج السطر الأول:
- t: إحصائية الاختبار وجدت أنها -1.428
- df: درجات الحرية، محسوبة على النحو n 1 + n 2 -2 = 12+12-2 = 22
- سيج. (ثنائي الذيل): القيمة p ثنائية الذيل والتي تتوافق مع قيمة -1.428 مع df=22
- فرق المتوسط: هو الفرق بين متوسطي العينتين
- معيار. خطأ الفرق: الخطأ المعياري لفرق المتوسط
- 95% CI للفرق: فاصل ثقة 95% للفرق الحقيقي بين متوسطي المجموعتين السكانيتين
وبما أن القيمة p للاختبار (0.167) لا تقل عن 0.05، فإننا نفشل في رفض الفرضية الصفرية. ليس لدينا ما يكفي من الأدلة لنقول أن متوسط ميلا في الغالون الحقيقي يختلف بين السيارات التي تتلقى العلاج والسيارات التي لا تفعل ذلك.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر