اختبار t للعينات المقترنة: التعريف والصيغة والمثال

يتم استخدام اختبار t للعينات المقترنة لمقارنة متوسطي عينتين عندما يمكن ربط كل ملاحظة في عينة واحدة بملاحظة في العينة الأخرى.

يشرح هذا البرنامج التعليمي ما يلي:

• الدافع لإجراء اختبار t للعينات المقترنة.
• صيغة إجراء اختبار t للعينات المقترنة.
• الافتراضات التي يجب توافرها لإجراء اختبار t للعينات المقترنة.
• مثال على كيفية إجراء اختبار t للعينات المقترنة.

اختبار t للعينات المقترنة: الدافع

يتم استخدام اختبار t للعينات المقترنة بشكل شائع في سيناريوهين:

1. يتم إجراء قياس على موضوع ما قبل وبعد العلاج – على سبيل المثال، يتم قياس الحد الأقصى للقفز العمودي للاعبي كرة السلة في الكلية قبل وبعد مشاركتهم في برنامج تدريبي.

2. يتم إجراء القياس في ظل حالتين مختلفتين – على سبيل المثال، يتم قياس زمن استجابة المريض باستخدام دواءين مختلفين.

في كلتا الحالتين، نريد مقارنة متوسط القياس بين مجموعتين حيث يمكن ربط كل ملاحظة من عينة واحدة بملاحظة من العينة الأخرى.

اختبار t للعينات المقترنة: الصيغة

يستخدم اختبار t للعينات المقترنة دائمًا فرضية العدم التالية:

• H ₀ : μ ₁ = μ ₂ (متوسطا السكان متساويان)

يمكن أن تكون الفرضية البديلة ثنائية أو يسارية أو يمينية:

• H ₁ (ثنائي الذيل): μ ₁ ≠ μ ₂ (متوسط المجموعتين غير متساويين)
• H ₁ (يسار): μ ₁ < μ ₂ (متوسط السكان 1 أقل من متوسط السكان 2)
• H ₁ (يمين): μ ₁ > μ ₂ (متوسط السكان 1 أكبر من متوسط السكان 2)

نستخدم الصيغة التالية لحساب إحصائية اختبار t:

ر = س _فرق / (ق _فرق /√ن)

ذهب:

• x _diff : مثال لمتوسط الاختلافات
• الصورة: مثال على الانحراف المعياري للاختلافات
• n: حجم العينة (أي عدد الأزواج)

إذا كانت القيمة p التي تتوافق مع إحصائية اختبار t بدرجات حرية (n-1) أقل من مستوى الأهمية المختار (الاختيارات الشائعة هي 0.10 و0.05 و0.01)، فيمكنك رفض فرضية العدم.

اختبار t للعينات المقترنة: الافتراضات

لكي تكون نتائج اختبار t للعينات المقترنة صحيحة، يجب استيفاء الافتراضات التالية:

• ينبغي اختيار المشاركين عشوائيا من السكان.
• يجب أن تكون الاختلافات بين الأزواج موزعة بشكل طبيعي تقريبًا.
• لا ينبغي أن يكون هناك قيم متطرفة في الاختلافات.

اختبار t للعينات المقترنة : مثال

لنفترض أننا نريد أن نعرف ما إذا كان برنامج تدريبي معين قادر على زيادة الحد الأقصى للقفز العمودي (بالبوصة) للاعبي كرة السلة في الكلية أم لا.

ولاختبار ذلك، يمكننا تعيين عينة عشوائية بسيطة مكونة من 20 لاعب كرة سلة جامعيًا وقياس كل قفزة من قفزاتهم العمودية القصوى. ثم يمكننا أن نجعل كل لاعب يستخدم البرنامج التدريبي لمدة شهر ثم نقيس أقصى قفزة عمودية له مرة أخرى في نهاية الشهر.

لتحديد ما إذا كان البرنامج التدريبي له تأثير فعليًا على الحد الأقصى للقفز العمودي، سنقوم بإجراء اختبار t للعينات المقترنة عند مستوى الأهمية α = 0.05 باستخدام الخطوات التالية:

الخطوة 1: حساب البيانات الموجزة للاختلافات.

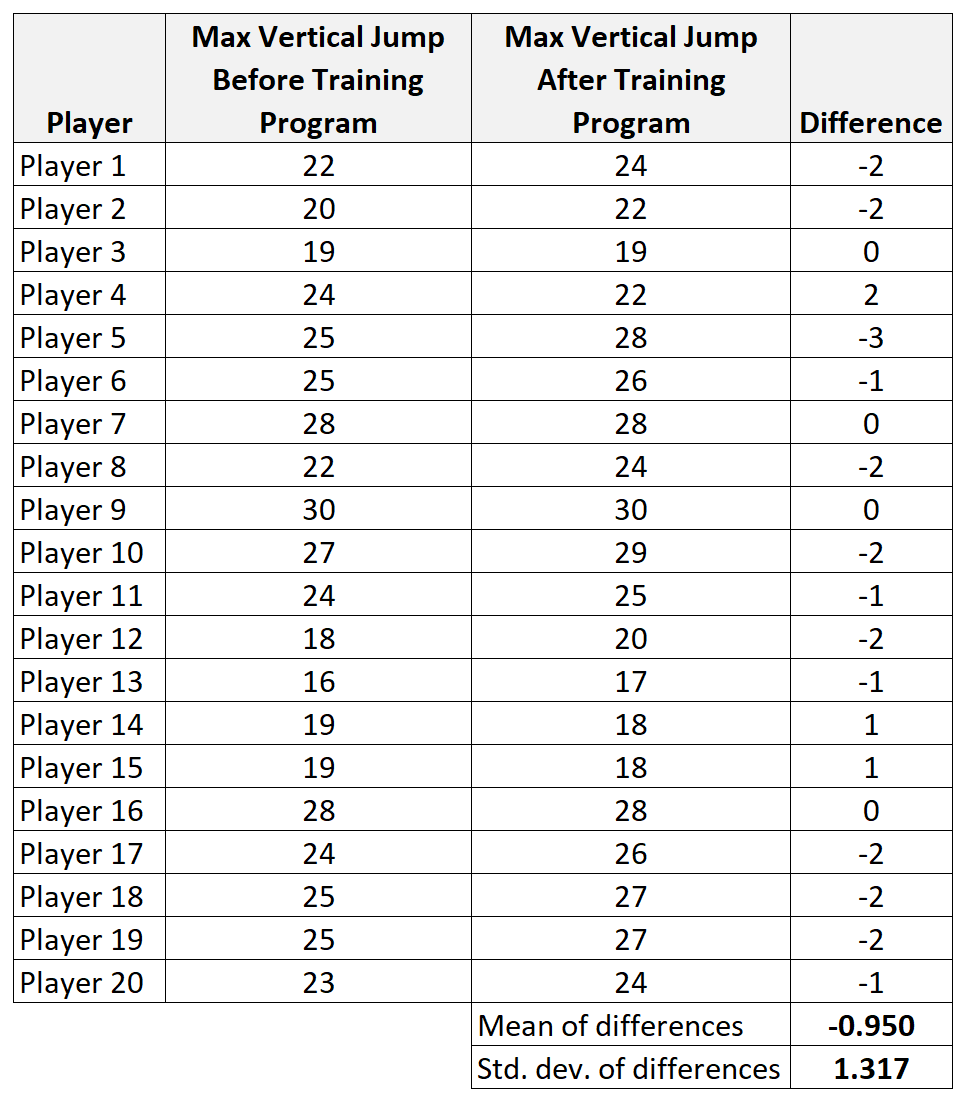
• x _diff : متوسط عينة الاختلافات = -0.95
• الصورة: عينة الانحراف المعياري للاختلافات = 1.317
• n: حجم العينة (أي عدد الأزواج) = 20

الخطوة الثانية: تحديد الافتراضات.

سوف نقوم بإجراء اختبار t للعينات المقترنة بالفرضيات التالية:

• H ₀ : μ ₁ = μ ₂ (متوسطا السكان متساويان)
• H ₁ : μ ₁ ≠ μ ₂ (وسطا السكان غير متساويين)

الخطوة 3: حساب إحصائية اختبار t .

t = x _فرق / (s _diff /√n) = -0.95 / (1.317/ √ 20) = -3.226

الخطوة 4: احسب القيمة الاحتمالية لإحصائيات اختبار t .

وفقًا لآلة حاسبة T Score to P Value ، فإن القيمة p المرتبطة بـ t = -3.226 ودرجات الحرية = n-1 = 20-1 = 19 هي 0.00445 .

الخطوة 5: استخلاص النتيجة.

وبما أن هذه القيمة p أقل من مستوى الأهمية لدينا α = 0.05، فإننا نرفض فرضية العدم. لدينا ما يكفي من الأدلة لنقول أن متوسط الحد الأقصى للقفز العمودي للاعبين يختلف قبل وبعد المشاركة في البرنامج التدريبي.

ملحوظة: يمكنك أيضًا إجراء اختبار t للعينات المقترنة بالكامل باستخدام حاسبة اختبار t للعينات المقترنة .

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء اختبار t للعينات المقترنة باستخدام برامج إحصائية مختلفة:

كيفية إجراء اختبار t للعينات المقترنة في Excel
كيفية إجراء اختبار t للعينات المقترنة في برنامج SPSS
كيفية إجراء اختبار t للعينات المقترنة في Stata
كيفية إجراء اختبار t للعينات المقترنة على الآلة الحاسبة TI-84
كيفية إجراء اختبار t للعينات المقترنة في R
كيفية إجراء اختبار t للعينات المقترنة في بايثون
كيفية إجراء اختبار T للعينات المقترنة يدويًا