اختبار z ثنائي النسبة: التعريف والصيغة والمثال

يتم استخدام اختبار z ثنائي النسبة لاختبار الفرق بين نسبتين سكانيتين.

يشرح هذا البرنامج التعليمي ما يلي:

• الدافع لإجراء اختبار z ثنائي النسبة.
• صيغة إجراء اختبار z ثنائي التناسب.
• مثال على كيفية إجراء اختبار z ثنائي التناسب.

اختبار Z ذو التناسبين: الدافع

لنفترض أننا نريد معرفة ما إذا كان هناك فرق بين نسبة السكان الذين يدعمون قانونًا معينًا في المقاطعة أ ونسبة الذين يدعمون القانون في المقاطعة ب.

نظرًا لوجود الآلاف من السكان في كل مقاطعة، سيكون الأمر مستهلكًا للوقت ومكلفًا للغاية للتجول ومسح كل فرد مقيم في كل مقاطعة.

بدلاً من ذلك، يمكننا أخذ عينة عشوائية بسيطة من السكان من كل مقاطعة واستخدام النسبة لصالح القانون في كل عينة لتقدير الفرق الحقيقي في النسب بين المقاطعتين:

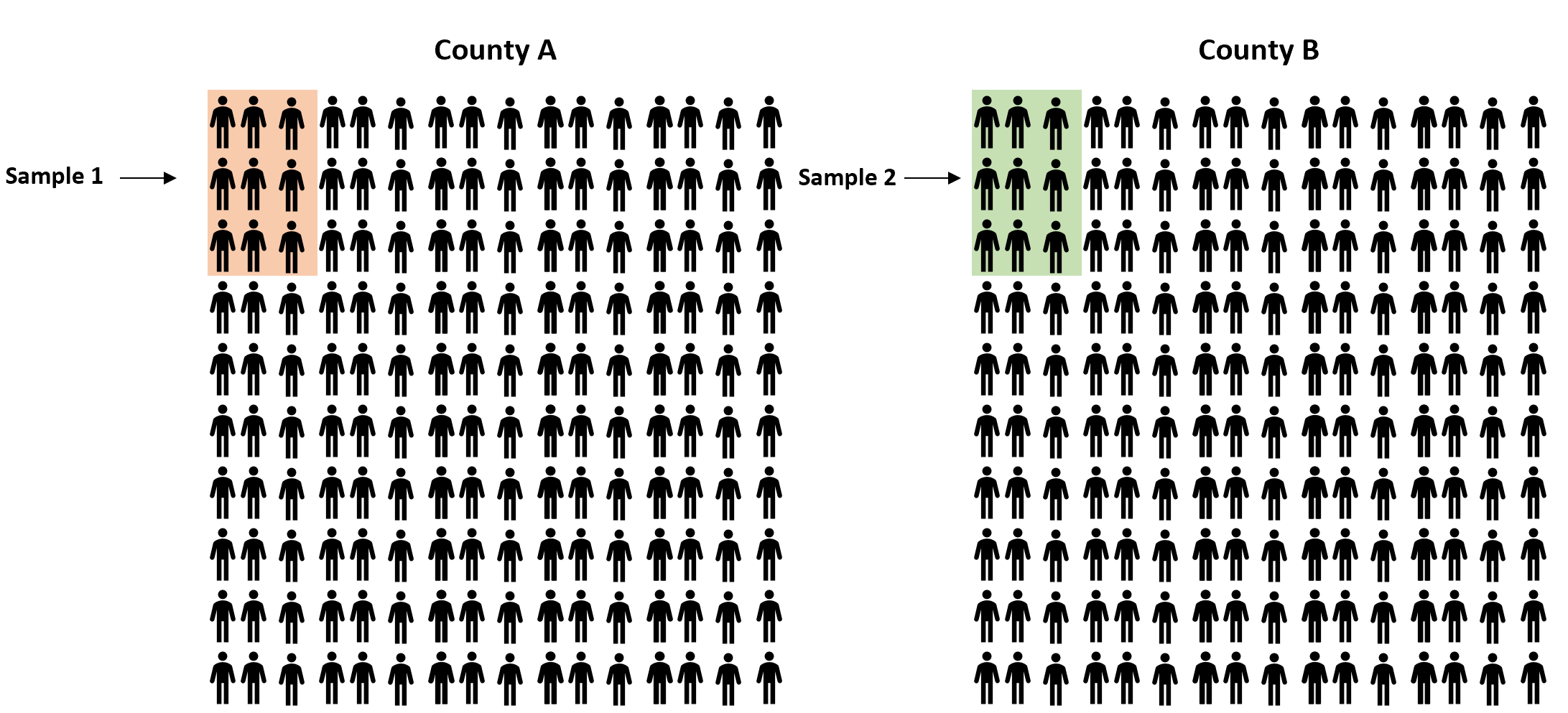
ومع ذلك، فمن المؤكد تقريبًا أن نسبة السكان المؤيدين للقانون ستكون مختلفة بعض الشيء على الأقل بين العينتين. والسؤال هو ما إذا كان هذا الاختلاف ذو دلالة إحصائية . ولحسن الحظ، فإن اختبار z ثنائي التناسب يسمح لنا بالإجابة على هذا السؤال.

اختبار Z ثنائي النسب: الصيغة

يستخدم اختبار z ثنائي النسب دائمًا فرضية العدم التالية:

• H ₀ : μ ₁ = μ ₂ (النسبتان السكانيتان متساويتان)

يمكن أن تكون الفرضية البديلة ثنائية أو يسارية أو يمينية:

• H ₁ (ثنائي الذيل): π ₁ ≠ π ₂ (النسبتان السكانيتان غير متساويتين)
• H ₁ (يسار): π ₁ < π ₂ (نسبة السكان 1 أقل من نسبة السكان 2)
• H ₁ (يمين): π ₁ > π ₂ (نسبة السكان 1 أكبر من نسبة السكان 2)

نستخدم الصيغة التالية لحساب إحصائية اختبار z:

ض = (ص ₁ -ص ₂ ) / √ ص(1-ص)(1/ن ₁ +1/ن ₂ )

حيث p ₁ وp ₂ هي نسب العينة، وn ₁ وn ₂ هي أحجام العينة، وحيث p هي النسبة الإجمالية المجمعة المحسوبة على النحو التالي:

ع = (ع ₁ ن ₁ + ص ₂ ن ₂ )/( ن ₁ + ن ₂ )

إذا كانت القيمة p التي تتوافق مع إحصائيات اختبار z أقل من مستوى الأهمية المختار (الاختيارات الشائعة هي 0.10 و0.05 و0.01)، فيمكنك رفض فرضية العدم.

اختبار Z بنسبتين : مثال

لنفترض أننا نريد معرفة ما إذا كان هناك فرق بين نسبة السكان الذين يدعمون قانونًا معينًا في المقاطعة أ ونسبة الذين يدعمون القانون في المقاطعة ب.

ولاختبار ذلك، سنقوم بإجراء اختبار z ثنائي التناسب عند مستوى الأهمية α = 0.05 باستخدام الخطوات التالية:

الخطوة 1: جمع بيانات العينة.

لنفترض أننا قمنا بجمع عينة عشوائية من السكان من كل مقاطعة وحصلنا على المعلومات التالية:

العينة 1:

• حجم العينة ن ₁ = 50
• النسبة لصالح القانون ع ₁ = 0.67

العينة 2:

• حجم العينة ن ₂ = 50
• النسبة لصالح القانون ع ₂ = 0.57

الخطوة الثانية: تحديد الافتراضات.

سنقوم بإجراء اختبار z ذو التناسبين مع الفرضيات التالية:

• H ₀ : π ₁ = π ₂ (النسبتان السكانيتان متساويتان)
• H ₁ : π ₁ ≠ π ₂ (النسبتان السكانيتان غير متساويتين)

الخطوة 3: حساب إحصائية اختبار z .

أولاً، سنقوم بحساب النسبة الإجمالية المجمعة:

ع = (ص ₁ ن ₁ + ص ₂ ن ₂ )/(ن ₁ +ن ₂ ) = (0.67(50) + 0.57(50))/(50+50) = 0.62

بعد ذلك، سوف نقوم بحساب إحصائية اختبار z :

ض = (ص ₁ -ص ₂ ) / √ ص(1-ص)(1/ن ₁ +1/ن ₂ ) = (.67-.57) / √ .62(1-.62)(1/50) + 1/50 ) = 1.03

الخطوة 4: احسب القيمة p لإحصائيات اختبار z .

وفقًا لآلة حاسبة P-value Z-score، فإن القيمة p ثنائية الطرف المرتبطة بـ z = 1.03 هي 0.30301 .

الخطوة 5: استخلاص النتيجة.

وبما أن هذه القيمة p ليست أقل من مستوى الأهمية لدينا α = 0.05، فإننا نفشل في رفض فرضية العدم. ليس لدينا أدلة كافية للقول بأن نسبة السكان المؤيدين لهذا القانون تختلف بين المقاطعتين.

ملحوظة: يمكنك أيضًا إجراء اختبار Z ثنائي النسب بأكمله ببساطة عن طريق استخدام حاسبة اختبار Z ثنائي النسب .

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء اختبار z ثنائي التناسب باستخدام برامج إحصائية متنوعة:

كيفية إجراء اختبار Z ثنائي التناسب في Excel
كيفية إجراء اختبار Z ثنائي النسبة في SAS
حاسبة اختبار النسبة Z