كيفية إجراء اختبار اتجاه مان كيندال في r

يتم استخدام اختبار اتجاه مان كيندال لتحديد ما إذا كان هناك اتجاه في بيانات السلاسل الزمنية أم لا. هذا اختبار غير معلمي، مما يعني أنه لا توجد افتراضات أساسية حول صحة البيانات.

فرضيات الاختبار هي كما يلي:

H ₀ (فرضية العدم): لا يوجد اتجاه في البيانات.

_HA (فرضية بديلة): هناك اتجاه موجود في البيانات. (قد يكون هذا اتجاها إيجابيا أو سلبيا)

إذا كانت القيمة p للاختبار أقل من مستوى معين من الأهمية (الاختيارات الشائعة هي 0.10 و0.05 و0.01)، فهناك دليل ذو دلالة إحصائية على وجود اتجاه في البيانات من السلسلة الزمنية.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار الاتجاه مان كيندال في R.

مثال: اختبار اتجاه مان كيندال في R

لإجراء اختبار اتجاه Mann-Kendall في لغة R، سنستخدم الدالة MannKendall() من مكتبة Kendall ، والتي تستخدم الصيغة التالية:

مان كيندال (x)

ذهب:

• x = متجه البيانات، غالبًا ما يكون سلسلة زمنية

لتوضيح كيفية إجراء الاختبار، سوف نستخدم مجموعة بيانات PrecipGL المدمجة في مكتبة كيندال ، والتي تحتوي على معلومات هطول الأمطار السنوية لجميع البحيرات العظمى من عام 1900 إلى عام 1986:

 #load Kendall library and PrecipGL dataset
library(Kendall)
data(PrecipGL)

#view dataset
PrecipGL

Time Series:
Start = 1900 
End = 1986 
Frequency = 1 
[1] 31.69 29.77 31.70 33.06 31.31 32.72 31.18 29.90 29.17 31.48 28.11 32.61
[13] 31.31 30.96 28.40 30.68 33.67 28.65 30.62 30.21 28.79 30.92 30.92 28.13
[25] 30.51 27.63 34.80 32.10 33.86 32.33 25.69 30.60 32.85 30.31 27.71 30.34
[37] 29.14 33.41 33.51 29.90 32.69 32.34 35.01 33.05 31.15 36.36 29.83 33.70
[49] 29.81 32.41 35.90 37.45 30.39 31.15 35.75 31.14 30.06 32.40 28.44 36.38
[61] 31.73 31.27 28.51 26.01 31.27 35.57 30.85 33.35 35.82 31.78 34.25 31.43
[73] 35.97 33.87 28.94 34.62 31.06 38.84 32.25 35.86 32.93 32.69 34.39 33.97
[85] 32.15 40.16 36.32
attr(,"title")
[1] Annual precipitation, 1900-1986, Entire Great Lakes

لمعرفة ما إذا كان هناك اتجاه في البيانات، يمكننا إجراء اختبار اتجاه مان كيندال:

 #Perform the Mann-Kendall Trend Test
MannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00029206

إحصائيات الاختبار هي 0.265 والقيمة p المقابلة ثنائية الطرف هي 0.00029206 . وبما أن هذه القيمة p أقل من 0.05، فسوف نرفض الفرضية الصفرية للاختبار ونستنتج أن هناك اتجاهًا موجودًا في البيانات.

لتصور هذا الاتجاه، يمكننا إنشاء مخطط زمني لهطول الأمطار السنوي سنويًا وإضافة خط سلس لتمثيل الاتجاه:

 #Plot the time series data
plot(PrecipGL)

#Add a smooth line to visualize the trend 
lines(lowess(time(PrecipGL),PrecipGL), col='blue')

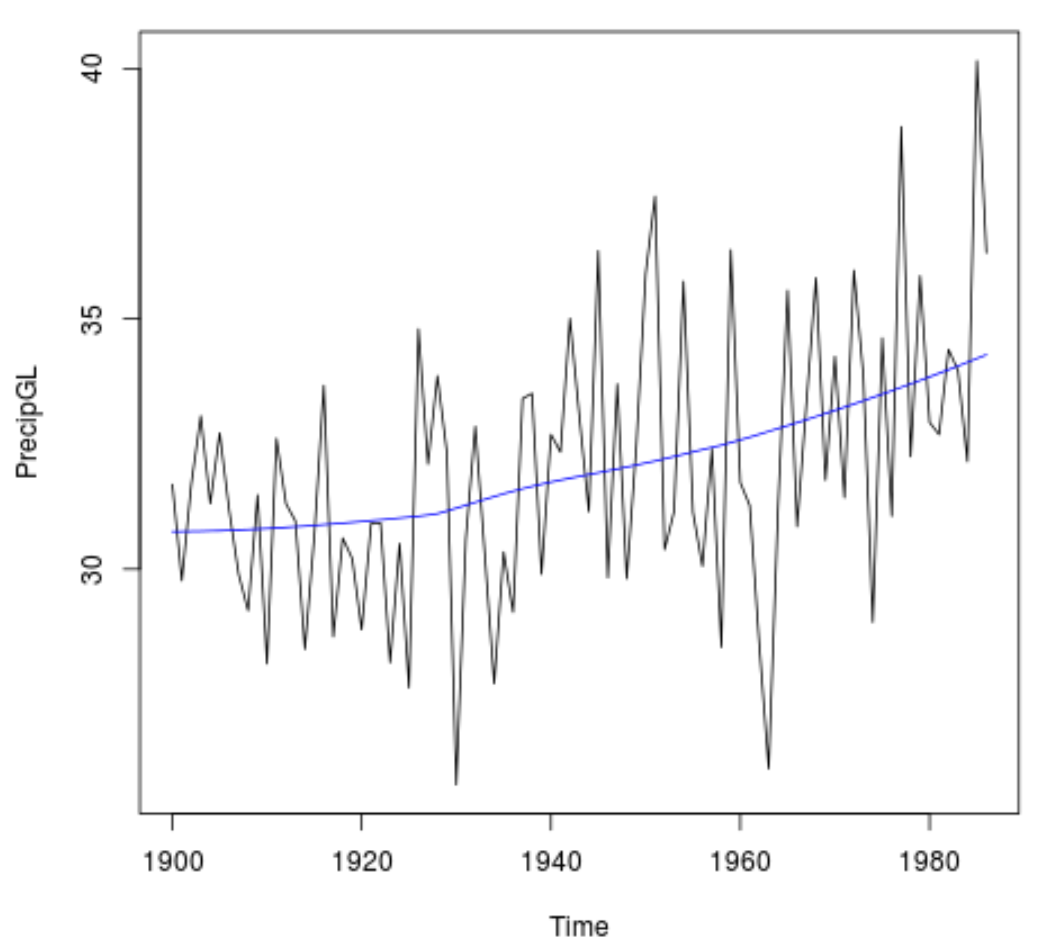
لاحظ أنه يمكننا أيضًا إجراء اختبار اتجاه Mann-Kendall المعدل موسميًا لمراعاة أي موسمية في البيانات باستخدام الأمر SeasonalMannKendall(x) :

 #Perform a seasonally-adjusted Mann-Kendall Trend Test
SeasonalMannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00028797

إحصائيات الاختبار هي 0.265 والقيمة p المقابلة ثنائية الطرف هي 0.00028797 . مرة أخرى، هذه القيمة p أقل من 0.05، لذلك سنرفض الفرضية الصفرية للاختبار ونستنتج أن هناك اتجاهًا موجودًا في البيانات.