كيفية إجراء اختبار z ثنائي النسبة في sas

يتم استخدام اختبار z ثنائي النسبة لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين نسبتين من السكان.

يستخدم هذا الاختبار الفرضية الصفرية التالية:

• H ₀ : μ ₁ = μ ₂ (النسبتان السكانيتان متساويتان)

يمكن أن تكون الفرضية البديلة ثنائية أو يسارية أو يمينية:

• H ₁ (ثنائي الذيل): π ₁ ≠ π ₂ (النسبتان السكانيتان غير متساويتين)
• H ₁ (يسار): π ₁ < π ₂ (نسبة السكان 1 أقل من نسبة السكان 2)
• H ₁ (يمين): π ₁ > π ₂ (نسبة السكان 1 أكبر من نسبة السكان 2)

نستخدم الصيغة التالية لحساب إحصائية اختبار z:

ض = (ص ₁ -ص ₂ ) / √ ص(1-ص)(1/ن ₁ +1/ن ₂ )

حيث p ₁ وp ₂ هي نسب العينة، وn ₁ وn ₂ هي أحجام العينة، وحيث p هي النسبة الإجمالية المجمعة المحسوبة على النحو التالي:

ع = (ع ₁ ن ₁ + ص ₂ ن ₂ )/( ن ₁ + ن ₂ )

إذا كانت القيمة p التي تتوافق مع إحصائيات اختبار z أقل من مستوى الأهمية المختار (الاختيارات الشائعة هي 0.10 و0.05 و0.01)، فيمكنك رفض فرضية العدم.

يوضح المثال التالي كيفية إجراء اختبار z ثنائي التناسب في SAS.

مثال: اختبار النسبة Z في SAS

لنفترض أننا نريد معرفة ما إذا كان هناك فرق بين نسبة السكان الذين يدعمون قانونًا معينًا في المقاطعة أ ونسبة الذين يدعمون القانون في المقاطعة ب.

ولاختبار ذلك، قمنا بجمع عينة عشوائية من 50 ساكنًا من كل مقاطعة وإحصاء عدد المؤيدين للقانون.

يوضح الكود التالي كيفية إنشاء مجموعة بيانات تلخص عدد السكان الذين يدعمون القانون في كل مقاطعة:

 /*create dataset*/
data my_data;
    input county $status $count;
    datalines ;
A Bracket 34
A Reject 16
B Bracket 29
B Reject 21
;
run ;

/*view dataset*/
proc print data =my_data;

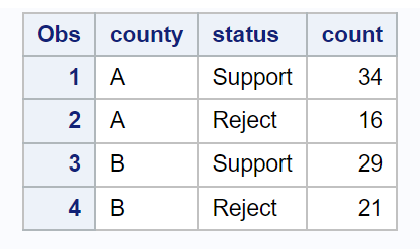
يمكننا بعد ذلك استخدام عبارة PROC FREQ مع الخيار Riskdiff (equal var = null) لإجراء اختبار z ثنائي التناسب:

 /*perform two proportion z-test*/
proc freq data =my_data;
    weightcount ;
    county tables * status / riskdiff ( equal var = null);
run ; 

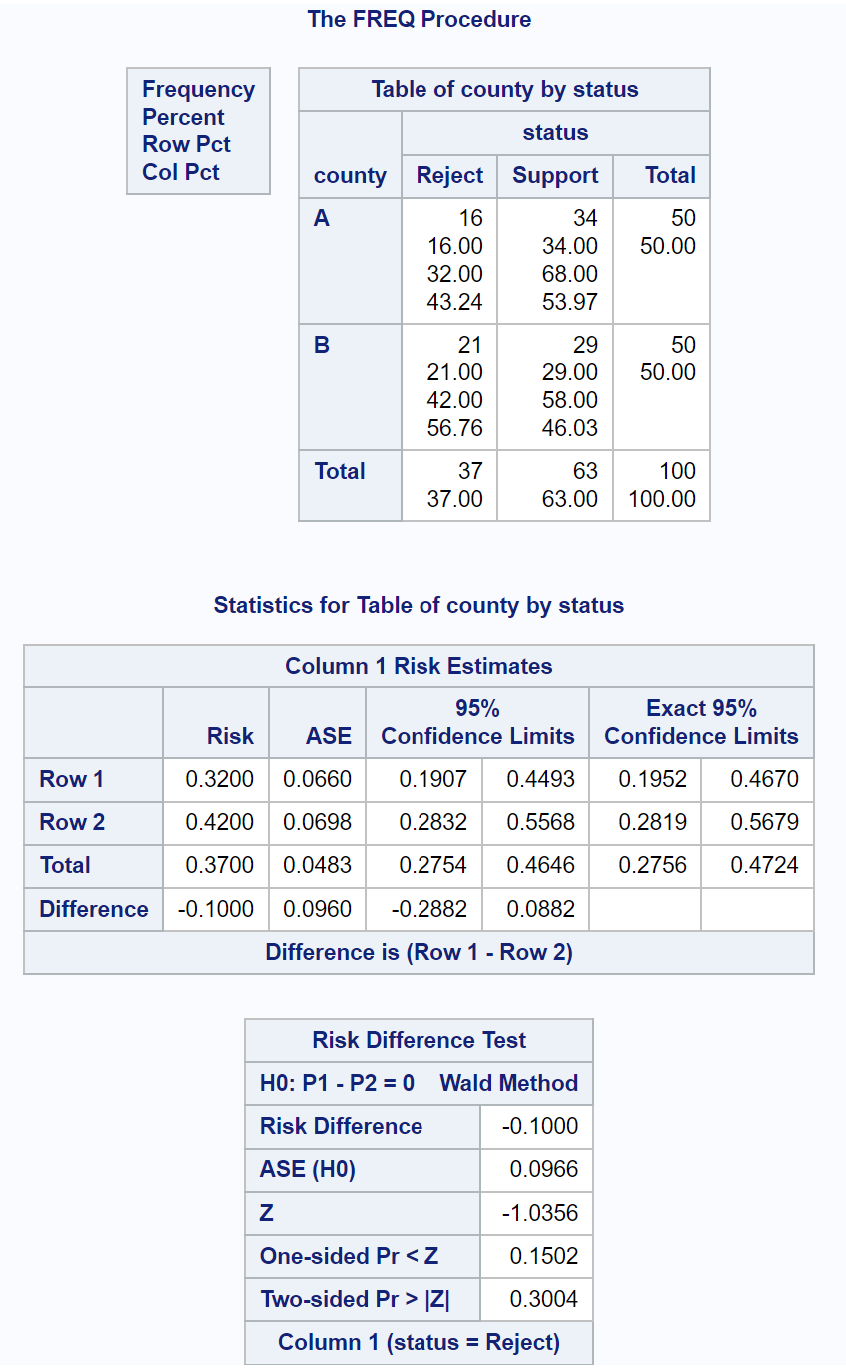
من جدول اختبار فرق المخاطر في النتيجة، يمكننا أن نرى المعلومات التالية:

• إحصائيات اختبار Z: -1.0356
• القيمة p على الوجهين: 0.3004

استخدم اختبار z ذو التناسبين هذا الافتراضات التالية:

• H ₀ : π ₁ = π ₂ (النسبتان السكانيتان متساويتان)
• H ₁ : π ₁ ≠ π ₂ (النسبتان السكانيتان غير متساويتين)

وبما أن القيمة p في المخرجات لا تقل عن 0.05، فإننا نفشل في رفض الفرضية الصفرية.

وهذا يعني أنه ليس لدينا أدلة كافية لنقول إن نسبة السكان الذين يؤيدون هذا القانون تختلف بين المقاطعتين.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء اختبارات إحصائية شائعة أخرى في SAS:

كيفية إجراء اختبار t لعينة واحدة في SAS
كيفية إجراء اختبار t لعينتين في SAS
كيفية إجراء اختبار t للعينات المقترنة في SAS