كيفية اختبار الحالة الطبيعية في r (4 طرق)

تفترض العديد من الاختبارات الإحصائية أن مجموعات البيانات يتم توزيعها بشكل طبيعي.

هناك أربع طرق شائعة للتحقق من هذا الافتراض في R:

1. (الطريقة المرئية) قم بإنشاء رسم بياني.

• إذا كان الرسم البياني على شكل “جرس” تقريبًا، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

2. (الطريقة المرئية) قم بإنشاء مخطط QQ.

• إذا كانت النقاط الموجودة على المخطط تقع تقريبًا على طول خط قطري مستقيم، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

3. (اختبار إحصائي رسمي) قم بإجراء اختبار شابيرو ويلك.

• إذا كانت القيمة p للاختبار أكبر من α = 0.05، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

4. (اختبار إحصائي رسمي) إجراء اختبار كولموجوروف-سميرنوف.

• إذا كانت القيمة p للاختبار أكبر من α = 0.05، فمن المفترض أن يتم توزيع البيانات بشكل طبيعي.

توضح الأمثلة التالية كيفية استخدام كل من هذه الطرق عمليًا.

الطريقة الأولى: إنشاء رسم بياني

يوضح الكود التالي كيفية إنشاء رسم بياني لمجموعة بيانات موزعة بشكل طبيعي وغير موزعة بشكل طبيعي في R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

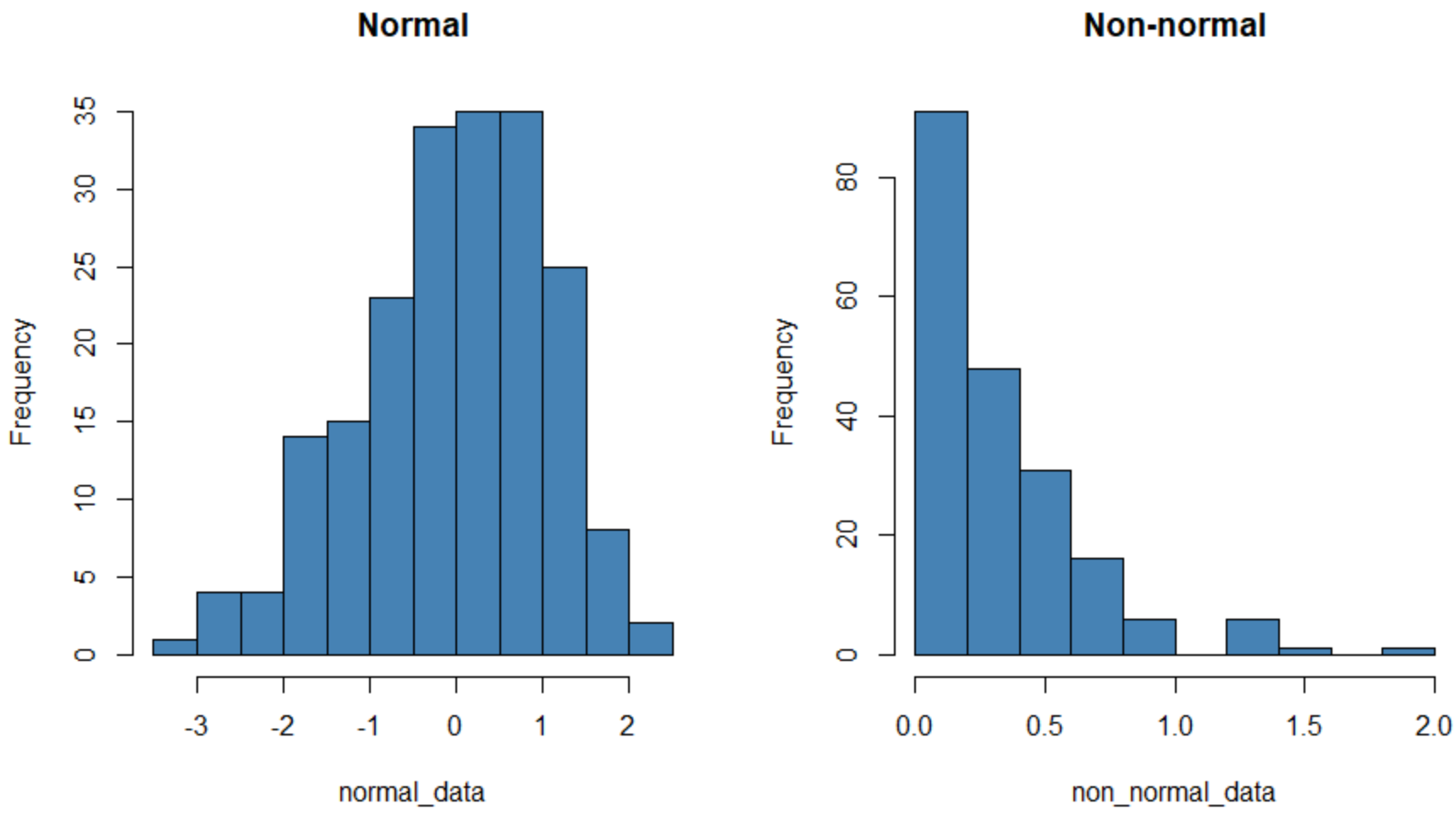
يُظهر الرسم البياني الموجود على اليسار مجموعة بيانات يتم توزيعها بشكل طبيعي (على شكل “جرس” تقريبًا) ويُظهر الرسم البياني الموجود على اليمين مجموعة بيانات لا يتم توزيعها بشكل طبيعي.

الطريقة الثانية: إنشاء مخطط QQ

يوضح الكود التالي كيفية إنشاء مخطط QQ لمجموعة بيانات موزعة بشكل طبيعي وغير موزعة بشكل طبيعي في R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

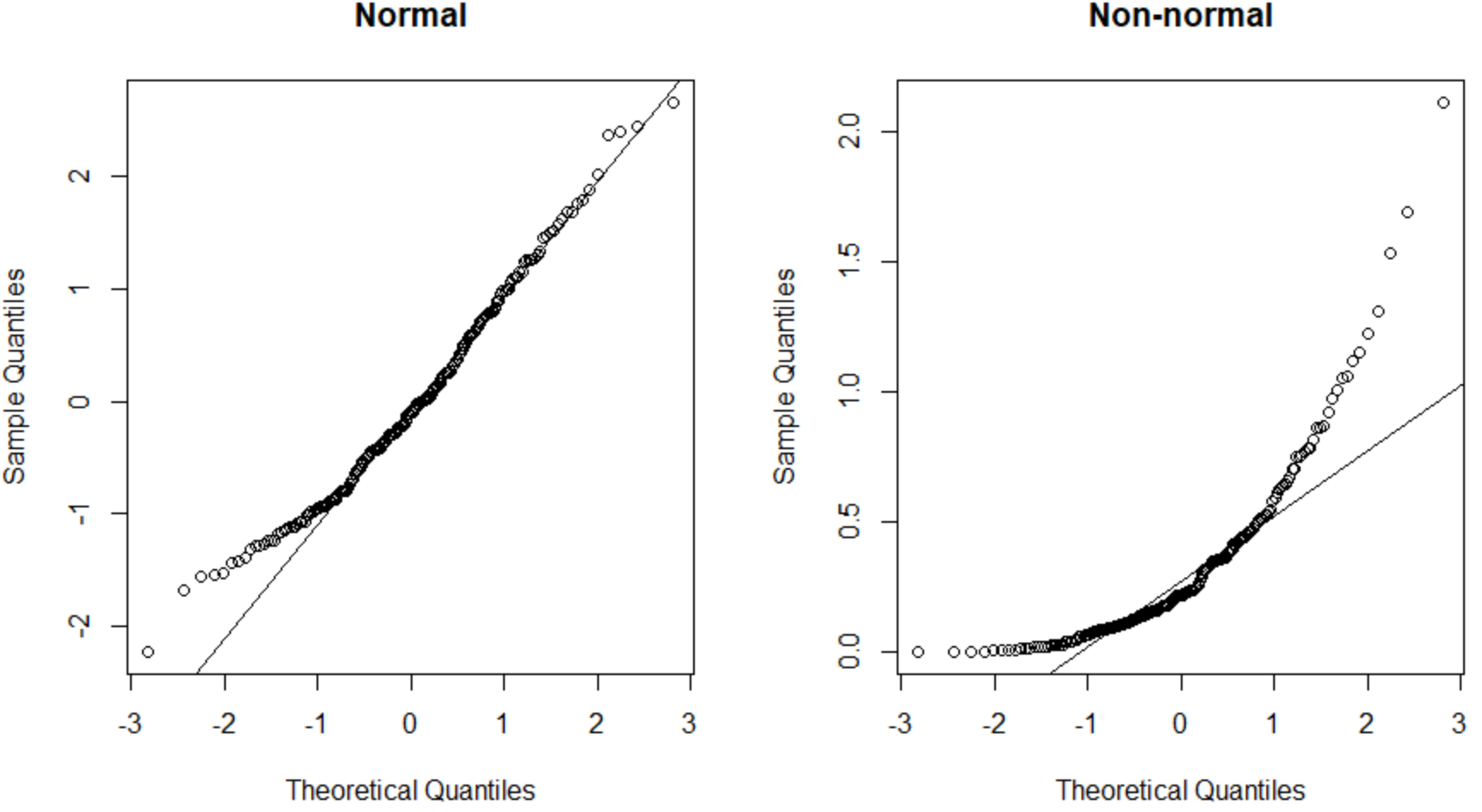
يعرض مخطط QQ الموجود على اليسار مجموعة بيانات يتم توزيعها بشكل طبيعي (تقع النقاط على طول خط قطري مستقيم) ويقدم مخطط QQ الموجود على اليمين مجموعة بيانات لا يتم توزيعها بشكل طبيعي.

الطريقة الثالثة: إجراء اختبار شابيرو ويلك

يوضح الكود التالي كيفية إجراء اختبار Shapiro-Wilk على مجموعة بيانات موزعة بشكل طبيعي وغير موزعة بشكل طبيعي في R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

القيمة p للاختبار الأول لا تقل عن 0.05، مما يشير إلى أن البيانات يتم توزيعها بشكل طبيعي.

القيمة p للاختبار الثاني أقل من 0.05، مما يشير إلى أن البيانات لا يتم توزيعها بشكل طبيعي.

الطريقة الرابعة: إجراء اختبار كولموجوروف-سميرنوف

يوضح الكود التالي كيفية إجراء اختبار Kolmogorov-Smirnov على مجموعة بيانات موزعة بشكل طبيعي وغير موزعة بشكل طبيعي في R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

القيمة p للاختبار الأول لا تقل عن 0.05، مما يشير إلى أن البيانات يتم توزيعها بشكل طبيعي.

القيمة p للاختبار الثاني أقل من 0.05، مما يشير إلى أن البيانات لا يتم توزيعها بشكل طبيعي.

كيفية التعامل مع البيانات غير العادية

إذا لم يتم توزيع مجموعة بيانات معينة بشكل طبيعي، فيمكننا غالبًا إجراء أحد التحويلات التالية لجعلها موزعة بشكل طبيعي أكثر:

1. تحويل السجل: تحويل قيم x إلى log(x) .

2. تحويل الجذر التربيعي: قم بتحويل قيم x إلى √x .

3. تحويل الجذر التكعيبي: تحويل قيم x إلى x ^1/3 .

ومن خلال إجراء هذه التحويلات، تصبح مجموعة البيانات موزعة بشكل طبيعي أكثر.

اقرأ هذا البرنامج التعليمي لمعرفة كيفية إجراء هذه التحولات في R.

مصادر إضافية

كيفية إنشاء الرسوم البيانية في R
كيفية إنشاء وتفسير مؤامرة QQ في R
كيفية إجراء اختبار شابيرو ويلك في R
كيفية إجراء اختبار Kolmogorov-Smirnov في R