كيفية إجراء اختبار شيفيه في sas

يتم استخدام ANOVA أحادي الاتجاه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات مستقلة أو أكثر أم لا.

إذا كانت القيمة الاحتمالية الإجمالية لجدول تحليل التباين (ANOVA) أقل من مستوى معين من الأهمية، فلدينا أدلة كافية لنقول أن إحدى وسائل المجموعة على الأقل تختلف عن الوسائل الأخرى.

ومع ذلك، هذا لا يخبرنا ما هي المجموعات التي تختلف عن بعضها البعض. وهذا يخبرنا ببساطة أنه ليست كل متوسطات المجموعة متساوية.

لكي نعرف بالضبط أي المجموعات تختلف عن بعضها البعض، نحتاج إلى إجراء اختبار لاحق .

أحد الاختبارات اللاحقة الأكثر استخدامًا هو اختبار شيف ، والذي يسمح لنا بإجراء مقارنات زوجية بين وسائل كل مجموعة مع التحكم في معدل الخطأ العائلي .

يوضح المثال التالي كيفية إجراء اختبار Scheffe في R.

مثال: اختبار شيفيه في SAS

لنفترض أن أحد الباحثين قام بتجنيد 30 طالبًا للمشاركة في إحدى الدراسات. يتم تعيين الطلاب بشكل عشوائي لاستخدام إحدى طرق الدراسة الثلاثة للتحضير للامتحان.

يمكننا استخدام الكود التالي لإنشاء مجموعة البيانات هذه في SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 76
At 77
At 77
At 81
At 82
At 82
At 83
At 84
At 85
At 89
B 81
B 82
B 83
B 83
B 83
B 84
B 87
B90
B92
B93
C 77
C 78
C 79
C 88
C 89
C 90
C 91
C 95
C 98
C 98
;
run ;

بعد ذلك، سوف نستخدم proc ANOVA لإجراء تحليل التباين أحادي الاتجاه:

 /*perform one-way ANOVA with Scheffe's post-hoc test*/
proc ANOVA data = my_data;
classMethod ;
modelScore = Method;
means Method / scheffe cldiff ;
run;

ملاحظة : استخدمنا بيان الوسائل جنبًا إلى جنب مع خيارات Scheffe و Cldiff لتحديد أنه يجب إجراء اختبار Scheffe اللاحق (مع فترات الثقة) إذا كانت القيمة p الإجمالية من ANOVA أحادية الاتجاه ذات دلالة إحصائية.

أولاً، سنقوم بتحليل جدول ANOVA في النتيجة:

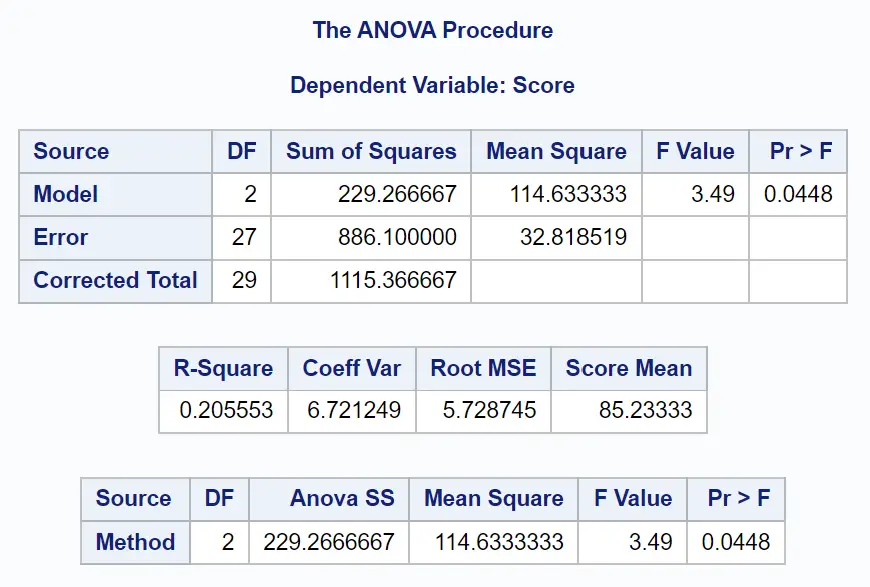
ومن هذا الجدول يمكننا أن نرى:

• القيمة F الإجمالية: 3.49
• القيمة p المقابلة: 0.0448

تذكر أن تحليل التباين أحادي الاتجاه يستخدم الفرضيات الصفرية والبديلة التالية:

• H ₀ : جميع وسائل المجموعة متساوية.
• _HA : يختلف متوسط مجموعة واحدة على الأقل   استراحة.

وبما أن القيمة p لجدول ANOVA (0.0448) أقل من α = 0.05، فإننا نرفض فرضية العدم.

وهذا يخبرنا أن متوسط درجات الامتحان ليس متساويًا عبر طرق الدراسة الثلاثة.

ذات صلة: كيفية تفسير قيمة F وقيمة P في ANOVA

لتحديد أي مجموعة تختلف بالضبط، نحتاج إلى الرجوع إلى جدول النتائج النهائية الذي يوضح نتائج اختبارات Scheffe اللاحقة:

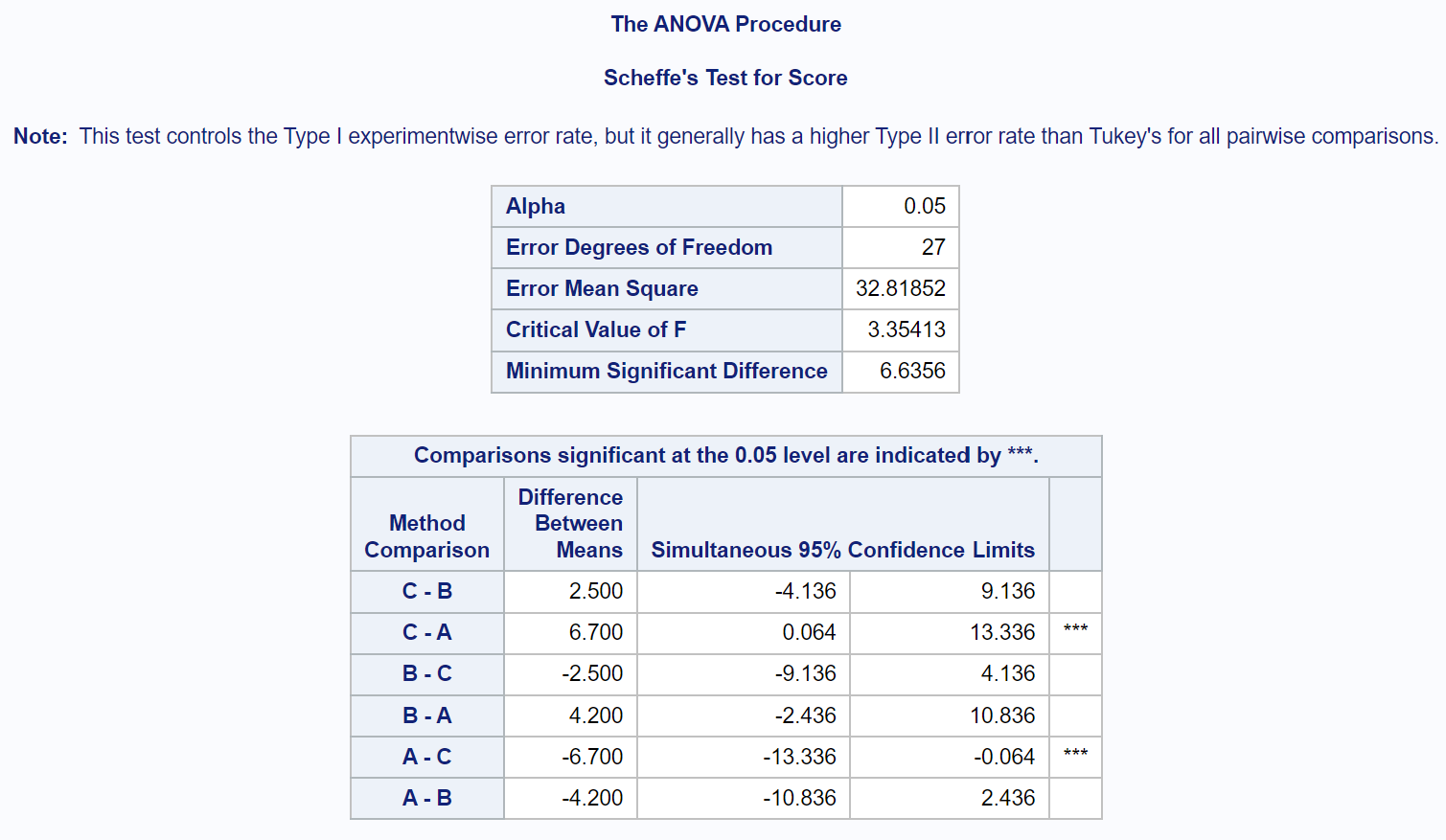
لمعرفة متوسطات المجموعات المختلفة، نحتاج إلى النظر في المقارنات الزوجية التي تحتوي على نجوم ( *** ) بجانبها.

ويوضح الجدول أن هناك فرقاً ذا دلالة إحصائية في متوسط درجات الامتحان بين المجموعة (أ) والمجموعة (ج).

لا توجد فروق ذات دلالة إحصائية بين متوسطات المجموعات الأخرى.

على وجه التحديد، يمكننا أن نرى أن متوسط الفرق في درجات الامتحان بين المجموعة (ج) والمجموعة (أ) هو 6.7 .

فاصل الثقة 95% للفرق في المتوسطات بين هذه المجموعات هو [0.064، 13.336] .

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول نماذج ANOVA:

دليل لاستخدام اختبار ما بعد المخصص مع ANOVA
كيفية إجراء ANOVA أحادي الاتجاه في SAS
كيفية إجراء ANOVA ثنائي الاتجاه في SAS