اختبار الفرضيات للمتوسط
تشرح هذه المقالة ماهية اختبار الفرضيات للمتوسط في الإحصائيات. وبالتالي، ستجد صيغة اختبار الفرضيات للمتوسط، بالإضافة إلى تمرين تم حله خطوة بخطوة.
ما هو اختبار الفرضيات للمتوسط؟
اختبار الفرضية للمتوسط هو طريقة إحصائية تستخدم لرفض أو رفض الفرضية الصفرية لمتوسط المجتمع.
وبشكل أكثر تحديدًا، يتضمن اختبار الفرضيات للمتوسط حساب إحصائية الاختبار ومقارنتها بالقيمة الحرجة لرفض الفرضية الصفرية أم لا.
وتجدر الإشارة إلى أن اختبارات الفرضيات لها أسماء مختلفة؛ في الإحصاء، يطلق عليها أيضًا اسم تناقضات الفرضيات، أو اختبارات الفرضيات، أو اختبارات الأهمية.
صيغة اختبار الفرضية للمتوسط
بعد ذلك سنرى كيف يتم حساب إحصائية اختبار الفرضية للمتوسط. ومع ذلك، فإن الصيغة تختلف قليلا اعتمادا على ما إذا كان التباين معروفا أم لا، لذلك سنرى أولا كيف يتم ذلك عندما يكون التباين معروفا ثم عندما يكون التباين غير معروف.
مع الانحراف المعروف
صيغة فرضية الاختبار للمتوسط ذو التباين المعروف هي:

ذهب:
-

هي إحصائية اختبار الفرضية للمتوسط.
-

هي وسيلة العينة.
-

هو متوسط القيمة المقترحة.
-

هو الانحراف المعياري للسكان.
-

هو حجم العينة.
بمجرد حساب إحصائية اختبار الفرضية للمتوسط، يجب تفسير النتيجة لرفض أو رفض الفرضية الصفرية:
- إذا كان اختبار الفرضية للمتوسط ذو وجهين، فسيتم رفض الفرضية الصفرية إذا كانت القيمة المطلقة للإحصاء أكبر من القيمة الحرجة Z α/2 .
- إذا كان اختبار الفرضية للمتوسط يتطابق مع الذيل الأيمن، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أكبر من القيمة الحرجة Z α .
- إذا كان اختبار الفرضية للمتوسط يطابق الذيل الأيسر، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أقل من القيمة الحرجة -Z α .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0e2ccadfc369eb7543b8f86dfccc528e_l3.png)
وفي هذه الحالة يتم الحصول على القيم الحرجة من جدول التوزيع الطبيعي الموحد .
مع تباين غير معروف
صيغة فرضية الاختبار للمتوسط ذو التباين غير المعروف هي:

ذهب:
-

هي إحصائية اختبار الفرضية للمتوسط، والتي يتم تعريفها من خلال توزيع الطالب .
-

هي وسيلة العينة.
-

هو متوسط القيمة المقترحة.
-

هو الانحراف المعياري للعينة.
-

هو حجم العينة.
كما كان من قبل، يجب تفسير النتيجة المحسوبة لإحصائية الاختبار بالقيمة الحرجة لرفض أو عدم فرضية العدم:
- إذا كان اختبار الفرضية للمتوسط ذو وجهين، فسيتم رفض الفرضية الصفرية إذا كانت القيمة المطلقة للإحصاء أكبر من القيمة الحرجة t α/2|n-1 .
- إذا كان اختبار الفرضية للمتوسط يتطابق مع الذيل الأيمن، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أكبر من القيمة الحرجة t α|n-1 .
- إذا كان اختبار الفرضية للمتوسط يتطابق مع الذيل الأيسر، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أقل من القيمة الحرجة -t α|n-1 .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
عندما يكون التباين غير معروف، يتم الحصول على قيم الاختبار الحرجة من جدول توزيع الطالب.
مثال من العالم الحقيقي لاختبار الفرضيات للمتوسط
لفهم مفهوم اختبار الفرضيات لمتوسط السكان بشكل كامل، يمكنك رؤية مثال واقعي لهذا النوع من اختبار الفرضيات أدناه.
- تدعي إحدى شركات التكنولوجيا أن بطارية الكمبيوتر المحمول الذي تبيعه تدوم لمدة 6 ساعات. نحن نتحقق مما إذا كانت هذه الفرضية خاطئة عن طريق إجراء اختبار فرضية بمستوى أهمية α = 0.05. للقيام بذلك، تقرر شراء 20 وحدة ومراقبة عمر البطارية لكل جهاز كمبيوتر (يتم التعبير عن القيم بالساعات):
5.2 5.9 7.1 4.2 6.5
8.5 4.6 6.8 6.9 5.8
5.1 6.5 7.0 5.3 6.2
5.7 6.6 7.5 5.1 6.1
وفي هذه الحالة تكون الفرضيات الصفرية والبديلة لاختبار الفرضيات حول المتوسط كما يلي:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-329ffe392783b8bee1eef642d1a45f53_l3.png)
من أجل تحديد إحصائية الاختبار، نحتاج أولاً إلى حساب متوسط العينة والانحراف المعياري للعينة:
![]()
نظرًا لأننا لا نعرف التباين السكاني، للحصول على إحصائية الاختبار، نحتاج إلى تطبيق صيغة اختبار الفرضيات للوسط ذي التباين غير المعروف:

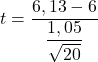
![]()
نحتاج الآن إلى إيجاد القيمة الحرجة لاختبار الفرضية، لذلك نبحث في جدول توزيع الطالب عن القيمة المقابلة. درجات حرية الطالب أقل بدرجة واحدة من حجم العينة (20-1=19) ومن ناحية أخرى فإن الاحتمال المقابل هو نصف مستوى الدلالة (0.05/2=0.025) لأنه ذو وجهين اختبار الفرضيات.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e85692dfb2fb2522025566dc205b8117_l3.png)
في الختام، بما أن هذا اختبار فرضي ذو وجهين والقيمة المطلقة لإحصائية الاختبار أقل من القيمة الحرجة، فلا يتم رفض الفرضية الصفرية، ولكن يتم رفض الفرضية البديلة.
![]()
اختبار الفرضيات للاختلاف في الوسائل
يستخدم اختبار فرضية الاختلاف في الوسائل لرفض أو قبول الفرضية الصفرية القائلة بأن متوسطات مجموعتين من السكان هي نفسها.
وبالتالي فإن الفرضية الصفرية لاختبار الفرضية للفرق بين وسيلتين هي دائمًا ما يلي:
![]()
في حين أن الفرضية البديلة يمكن أن تكون إحدى الفرضيات الثلاثة التالية:
![Rendered by QuickLaTeX.com \begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c612ac7651faad9faa195f37fdf6edef_l3.png)
ثم تكون صيغة حساب إحصائية اختبار الفرضية للفرق في المتوسطات عند معرفة التباين هي:
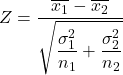
ذهب:
-

هي إحصائية اختبار الفرضية للفرق بين وسطين لهما تباين معروف، والذي يتبع التوزيع الطبيعي القياسي.
-

هو متوسط العينة 1.
-

هو متوسط العينة 2.
-

هو التباين السكاني 1.
-

هو التباين السكاني 2.
-

حجم العينة 1.
-

حجم العينة 2.
ومن ناحية أخرى فإن صيغة حساب إحصائية اختبار الفرضية للفرق في المتوسطات عندما يكون التباين غير معروف هي كما يلي:
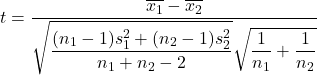
ذهب:
-

هي إحصائية اختبار الفرضية للفرق بين وسيلتين مع تباين غير معروف، والذي يتبع توزيع الطالب.
-

هو متوسط العينة 1.
-

هو متوسط العينة 2.
-

هو تباين العينة 1.
-

هو تباين العينة 2.
-

حجم العينة 1.
-

حجم العينة 2.