اختبار الفرضية للتناسب
تشرح هذه المقالة نسبة اختبار الفرضيات في الإحصائيات. لذلك، ستجد صيغة اختبار الفرضيات للنسبة، بالإضافة إلى تمرين خطوة بخطوة لفهم كيفية القيام بذلك بشكل كامل.
ما هو اختبار الفرضية للنسبة؟
اختبار فرضية النسبة هو طريقة إحصائية تستخدم لتحديد ما إذا كان سيتم رفض الفرضية الصفرية لنسبة السكان أم لا.
لذلك، اعتمادًا على قيمة إحصائية اختبار الفرضية للنسبة ومستوى الأهمية، يتم رفض الفرضية الصفرية أو قبولها.
لاحظ أن اختبار الفرضيات قد يُطلق عليه أيضًا اسم تناقضات الفرضيات، أو اختبار الفرضيات، أو اختبار الأهمية.
صيغة اختبار الفرضية للنسبة
إحصائية اختبار الفرضية للنسبة تساوي الفرق في نسبة العينة مطروحًا منها القيمة المقترحة للنسبة مقسومة على الانحراف المعياري للنسبة.
وبالتالي فإن صيغة فرضية الاختبار للنسبة هي:

ذهب:
-

هو اختبار الفرضية الإحصائية للنسبة.
-

هي نسبة العينة
-

هي قيمة النسبة المقترحة.
-

هو حجم العينة.
-

هو الانحراف المعياري للنسبة.
ضع في اعتبارك أنه لا يكفي حساب إحصائية اختبار الفرضية للنسبة، ولكن يجب بعد ذلك تفسير النتيجة:
- إذا كان اختبار الفرضية للنسبة ذو وجهين، فسيتم رفض الفرضية الصفرية إذا كانت القيمة المطلقة للإحصاء أكبر من القيمة الحرجة Z α/2 .
- إذا كان اختبار الفرضية للنسبة يتطابق مع الذيل الأيمن، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أكبر من القيمة الحرجة Z α .
- إذا كان اختبار الفرضية للنسبة يطابق الذيل الأيسر، فسيتم رفض الفرضية الصفرية إذا كانت الإحصائية أقل من القيمة الحرجة -Z α .
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
تذكر أنه يمكن الحصول على القيم الحرجة بسهولة من جدول التوزيع الطبيعي.
مثال على اختبار الفرضية للنسبة
بمجرد أن نرى تعريف اختبار الفرضيات للتناسب وما هي صيغته، سنحل مثالاً لفهم المفهوم بشكل أفضل.
- وفقا للشركة المصنعة له، فإن الدواء ضد مرض معين فعال بنسبة 70٪. وفي المختبر نقوم باختبار فعالية هذا الدواء حيث يعتقد الباحثون أن النسبة مختلفة. ولهذا تم اختبار الدواء على عينة مكونة من 1000 مريض وتم شفاء 641 شخصًا. إجراء اختبار فرضي على نسبة السكان بمستوى دلالة 5% لرفض أو عدم رفض فرضية الباحثين.
وفي هذه الحالة تكون الفرضية الصفرية والفرضية البديلة لاختبار الفرضيات لنسبة السكان هي:
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
نسبة الأشخاص في العينة الذين تم شفاؤهم بالدواء هي:
![]()
نقوم بحساب إحصائية اختبار الفرضية للنسبة من خلال تطبيق الصيغة الموضحة أعلاه:
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
من ناحية أخرى، بما أن مستوى الأهمية هو 0.05 وهذا اختبار فرضية ثنائي الطرف، فإن القيمة الحرجة للاختبار هي 1.96.
![]()
وفي الختام فإن القيمة المطلقة لإحصائية الاختبار أكبر من القيمة الحرجة لذلك نرفض الفرضية الصفرية ونقبل الفرضية البديلة.
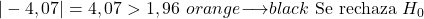 ➤ انظر: اختبار الفرضية للوسط
➤ انظر: اختبار الفرضية للوسط
اختبار الفرضيات لنسب العينتين
يتم استخدام اختبار الفرضية لنسب عينتين لرفض أو قبول الفرضية الصفرية القائلة بأن نسب مجموعتين مختلفتين متساويتين.
وبالتالي، فإن الفرضية الصفرية لاختبار الفرضية لنسب العينتين تكون دائمًا:
![]()
بينما الفرضية البديلة يمكن أن تكون أحد ثلاثة خيارات:
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
وصيغة حساب إحصائية اختبار الفرضية لنسب العينتين هي:
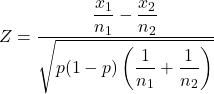
ذهب:
-

هي إحصائية اختبار الفرضية لنسب العينتين.
-
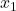
هو عدد النتائج في العينة 1.
-
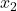
هو عدد النتائج في العينة 2.
-

حجم العينة 1.
-

حجم العينة 2.
-

هي النسبة المجمعة للعينتين.
اختبار الفرضيات لنسب العينة k
في اختبار الفرضيات حول نسب العينات k، يكون الهدف هو تحديد ما إذا كانت جميع نسب المجموعات السكانية المختلفة متساوية أو، على العكس من ذلك، ما إذا كانت هناك نسب مختلفة. وعليه فإن الفرضية الصفرية والفرضية البديلة في هذه الحالة هما:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
وفي هذه الحالة، يتم حساب النسبة المجمعة لجميع العينات على النحو التالي:
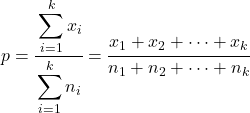
صيغة العثور على إحصائية اختبار الفرضية لنسب العينة k هي:
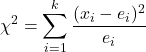
![]()
ذهب:
-

هي إحصائية اختبار الفرضية لنسب العينة k. في هذه الحالة، تتبع الإحصائية توزيع مربع كاي.
-

هو عدد النتائج في العينة i.
-

هو حجم العينة أنا.
-

هي النسبة المجمعة لجميع العينات.
-

هو عدد الزيارات المتوقعة من العينة i. ويتم حسابه بضرب النسبة المجمعة

حسب حجم العينة

.