كيفية اختبار أهمية منحدر الانحدار

لنفترض أن لدينا مجموعة البيانات التالية التي توضح المساحة بالقدم المربع وسعر 12 منزلًا مختلفًا:

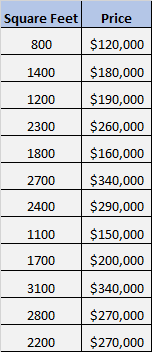
نريد أن نعرف ما إذا كانت هناك علاقة ذات دلالة إحصائية بين المساحة بالمتر المربع والسعر.

للحصول على فكرة عن شكل البيانات، نقوم أولاً بإنشاء مخطط انتشار بالقدم المربع على المحور السيني والسعر على المحور الصادي:

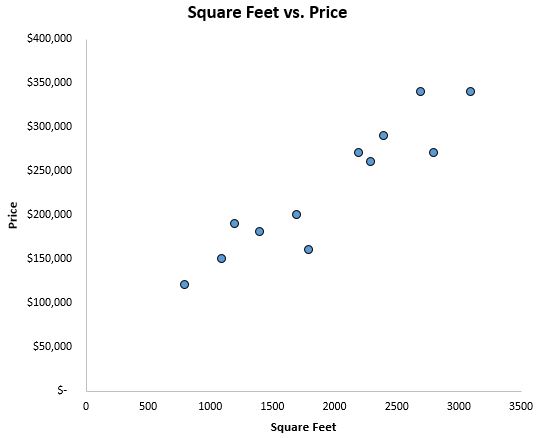
يمكننا أن نرى بوضوح أن هناك علاقة إيجابية بين المساحة بالمتر المربع والسعر. مع زيادة المساحة بالمتر المربع، يميل سعر المنزل أيضًا إلى الارتفاع.

ومع ذلك، لمعرفة ما إذا كانت هناك علاقة ذات دلالة إحصائية بين اللقطات المربعة والسعر، نحتاج إلى تشغيل انحدار خطي بسيط.

لذلك نقوم بتشغيل انحدار خطي بسيط باستخدام القدم المربعة كمؤشر والسعر كاستجابة ونحصل على النتيجة التالية:

سواء قمت بتشغيل انحدار خطي بسيط في Excel أو SPSS أو R أو أي برنامج آخر، فسوف تحصل على نتيجة مشابهة لتلك الموضحة أعلاه.

تذكر أن الانحدار الخطي البسيط سينتج الخط الأكثر ملاءمة، وهو معادلة الخط الذي “يناسب” البيانات في مخطط التشتت الخاص بنا. يتم تعريف هذا الخط من أفضل ملاءمة على النحو التالي:

ŷ = ب ₀ + ب ₁ س

حيث ŷ هي القيمة المتوقعة لمتغير الاستجابة، وb ₀ هو التقاطع، وb ₁ هو معامل الانحدار، وx هي قيمة متغير التوقع.

يتم إعطاء قيمة b ₀ بواسطة معامل الأصل، وهو 47588.70.

يتم إعطاء قيمة b ₁ بواسطة معامل المتغير المتوقع Square Feet وهو 93.57.

لذا فإن الخط الأنسب في هذا المثال هو ŷ = 47588.70+ 93.57x

إليك كيفية تفسير هذا السطر الأفضل ملاءمة:

• ب ₀ : عندما تكون قيمة القدم المربعة صفر، فإن متوسط قيمة السعر المتوقع هو 47,588.70 دولارًا. (في هذه الحالة، ليس من المنطقي حقًا تفسير التقاطع، نظرًا لأن المنزل لا يمكن أن تبلغ مساحته صفر قدم مربع أبدًا)
• ب ₁ : لكل قدم مربع إضافي، متوسط الزيادة المتوقعة في السعر هو 93.57 دولارًا.

إذن، نحن نعلم الآن أنه لكل قدم مربع إضافي، فإن متوسط الزيادة المتوقعة في السعر هو 93.57 دولارًا.

لمعرفة ما إذا كانت هذه الزيادة ذات دلالة إحصائية، نحتاج إلى إجراء اختبار فرضي لـ B ₁ أو إنشاء فاصل ثقة لـ B ₁ .

ملحوظة : اختبار الفرضية وفاصل الثقة سيعطيان دائمًا نفس النتائج.

بناء فاصل الثقة لمنحدر الانحدار

لإنشاء فاصل ثقة لمنحدر الانحدار، نستخدم الصيغة التالية:

فترة الثقة = b ₁ +/- (t _{1-∝/2, n-2} ) * (الخطأ المعياري b ₁ )

ذهب:

• b ₁ هو معامل الميل الوارد في نتيجة الانحدار
• (t _{1-∝/2, n-2} ) هي قيمة t الحرجة لمستوى الثقة 1-∝ مع درجات الحرية n-2 حيث n هو إجمالي عدد الملاحظات في مجموعة البيانات الخاصة بنا
• (الخطأ المعياري لـ b ₁ ) هو الخطأ المعياري لـ b ₁ الوارد في نتيجة الانحدار

على سبيل المثال، إليك كيفية إنشاء فاصل ثقة 95% لـ B ₁ :

• b ₁ هو 93.57 من مخرجات الانحدار.
• بما أننا نستخدم فاصل ثقة 95%، ∝ = 0.05 و n-2 = 12-2 = 10، إذن t _{0.975، 10} يساوي 2.228 وفقًا لجدول توزيع t
• (الخطأ القياسي لـ _b1 ) هو 11.45 من مخرجات الانحدار

وبالتالي، فإن فترة الثقة 95% الخاصة بنا لـ B ₁ هي:

93.57 +/- (2.228) * (11.45) = (68.06، 119.08)

وهذا يعني أننا واثقون بنسبة 95% من أن متوسط الزيادة الحقيقية في السعر لكل قدم مربع إضافي يتراوح بين 68.06 دولارًا و119.08 دولارًا.

لاحظ أن 0 دولار ليس موجودًا في هذه الفترة، وبالتالي فإن العلاقة بين اللقطات المربعة والسعر تكون ذات دلالة إحصائية عند مستوى ثقة 95%.

إجراء اختبار الفرضية لمنحدر الانحدار

لإجراء اختبار فرضية لمنحدر الانحدار، نتبع الخطوات الخمس القياسية لأي اختبار فرضية :

الخطوة 1. اذكر الفرضيات.

الفرضية الصفرية (H0): ب ₁ = 0

الفرضية البديلة: (ها): ب ₁ ≠ 0

الخطوة 2. تحديد مستوى الأهمية لاستخدامه.

وبما أننا أنشأنا فاصل ثقة بنسبة 95% في المثال السابق، فسوف نستخدم النهج المكافئ هنا ونختار استخدام مستوى أهمية قدره 0.05.

الخطوة 3. ابحث عن إحصائية الاختبار والقيمة الاحتمالية المقابلة لها.

في هذه الحالة، تكون إحصائية الاختبار هي t = معامل b ₁ / الخطأ المعياري لـ b ₁ مع درجات حرية n-2. يمكننا العثور على هذه القيم من نتيجة الانحدار:

وبالتالي فإن إحصائية الاختبار t = 92.89 / 13.88 = 6.69.

باستخدام حاسبة T من الدرجة إلى P value بنتيجة 6.69 مع 10 درجات من الحرية واختبار ثنائي الطرف، تكون القيمة p = 0.000 .

الخطوة 4. ارفض أو لا ترفض فرضية العدم.

وبما أن القيمة p أقل من مستوى الأهمية لدينا وهو 0.05، فإننا نرفض الفرضية الصفرية.

الخطوة 5. تفسير النتائج.

وبما أننا رفضنا فرضية العدم، فلدينا ما يكفي من الأدلة لنقول إن متوسط الزيادة الحقيقية في السعر لكل قدم مربع إضافي ليس صفرًا.