كيفية إجراء اختبارات t في جداول بيانات google

بشكل عام، هناك ثلاثة أنواع من اختبارات t:

• عينة من اختبار t
• اختبار T لعينتين
• اختبار t للعينات المقترنة

يقدم هذا البرنامج التعليمي أمثلة حول كيفية إجراء كل من هذه الاختبارات في جداول بيانات Google.

مثال: اختبار t لعينة واحدة

التعريف: يتم استخدام اختبار t لعينة واحدة لاختبار ما إذا كان متوسط المجتمع يساوي قيمة معينة أم لا.

مثال: يريد عالم النبات معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة. أخذت عينة عشوائية من 12 نباتًا وسجلت ارتفاع كل منها بالبوصة.

توضح لقطة الشاشة التالية كيفية إجراء اختبار t لعينة واحدة لتحديد ما إذا كان متوسط ارتفاع السكان الحقيقي يساوي 15 بوصة:

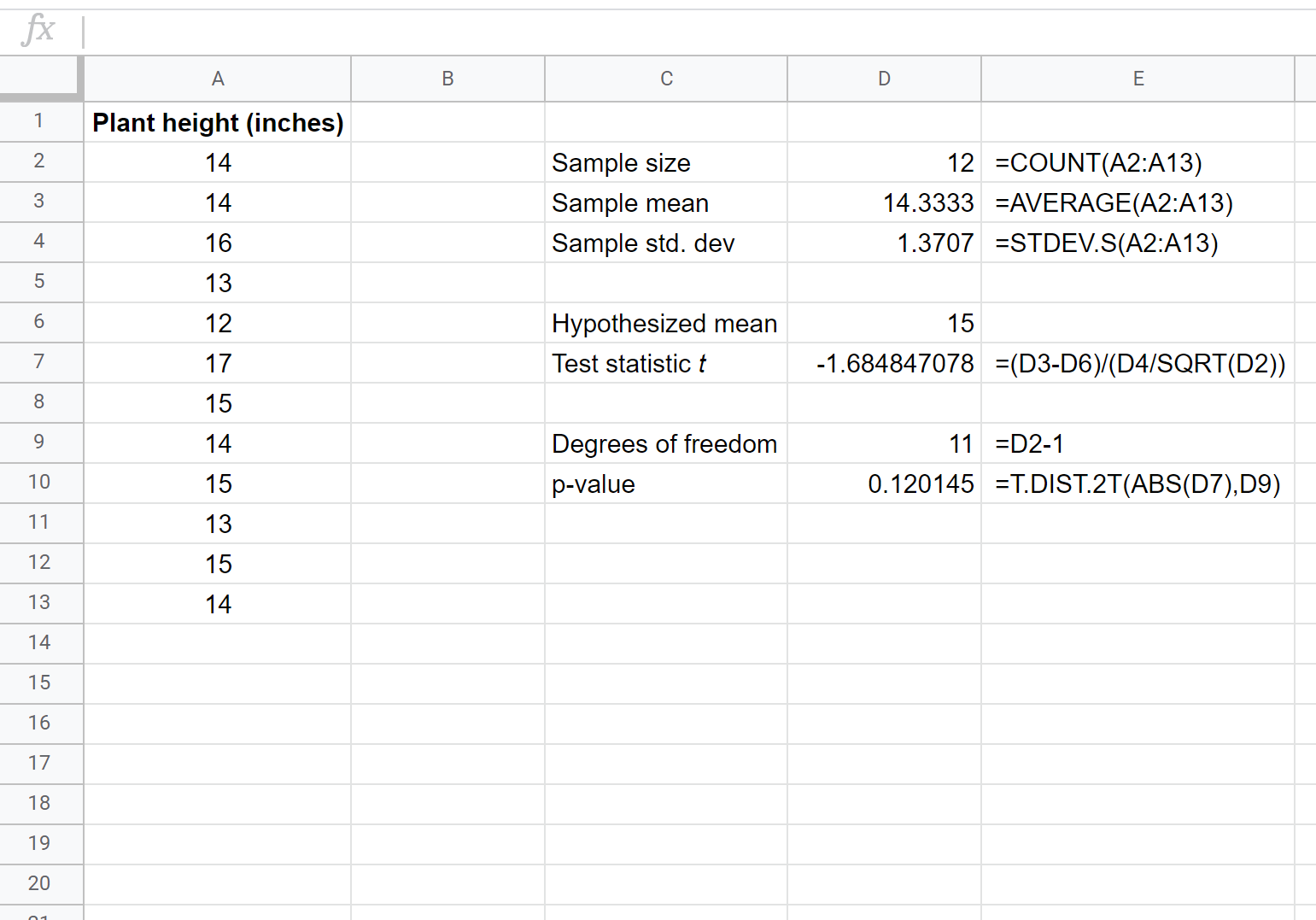
الفرضيتين لهذا الاختبار t على عينة معينة هي كما يلي:

H ₀ : μ = 15 (متوسط ارتفاع هذا النوع من النباتات هو 15 بوصة)

H _A : μ ≠15 (متوسط الارتفاع ليس 15 بوصة)

نظرًا لأن القيمة p للاختبار (0.120145) أكبر من alpha = 0.05، فإننا نفشل في رفض الفرضية الصفرية للاختبار. ليس لدينا أدلة كافية لنقول أن متوسط ارتفاع هذا النوع بالذات من النباتات هو أكثر من 15 بوصة.

مثال: اختبار t لعينتين

التعريف: يتم استخدام اختبار t المكون من عينتين لاختبار ما إذا كانت متوسطات مجتمعين متساويتين أم لا.

مثال: يريد الباحثون معرفة ما إذا كان هناك نوعان مختلفان من النباتات في بلد معين لهما نفس متوسط الارتفاع. قاموا بجمع عينة عشوائية من 20 نباتًا من كل نوع وسجلوا ارتفاع كل نبات بالبوصة.

توضح لقطة الشاشة التالية كيفية إجراء اختبار t لعينتين باستخدام الدالة T.TEST() لتحديد ما إذا كان متوسط ارتفاع المجموعتين متساويين:

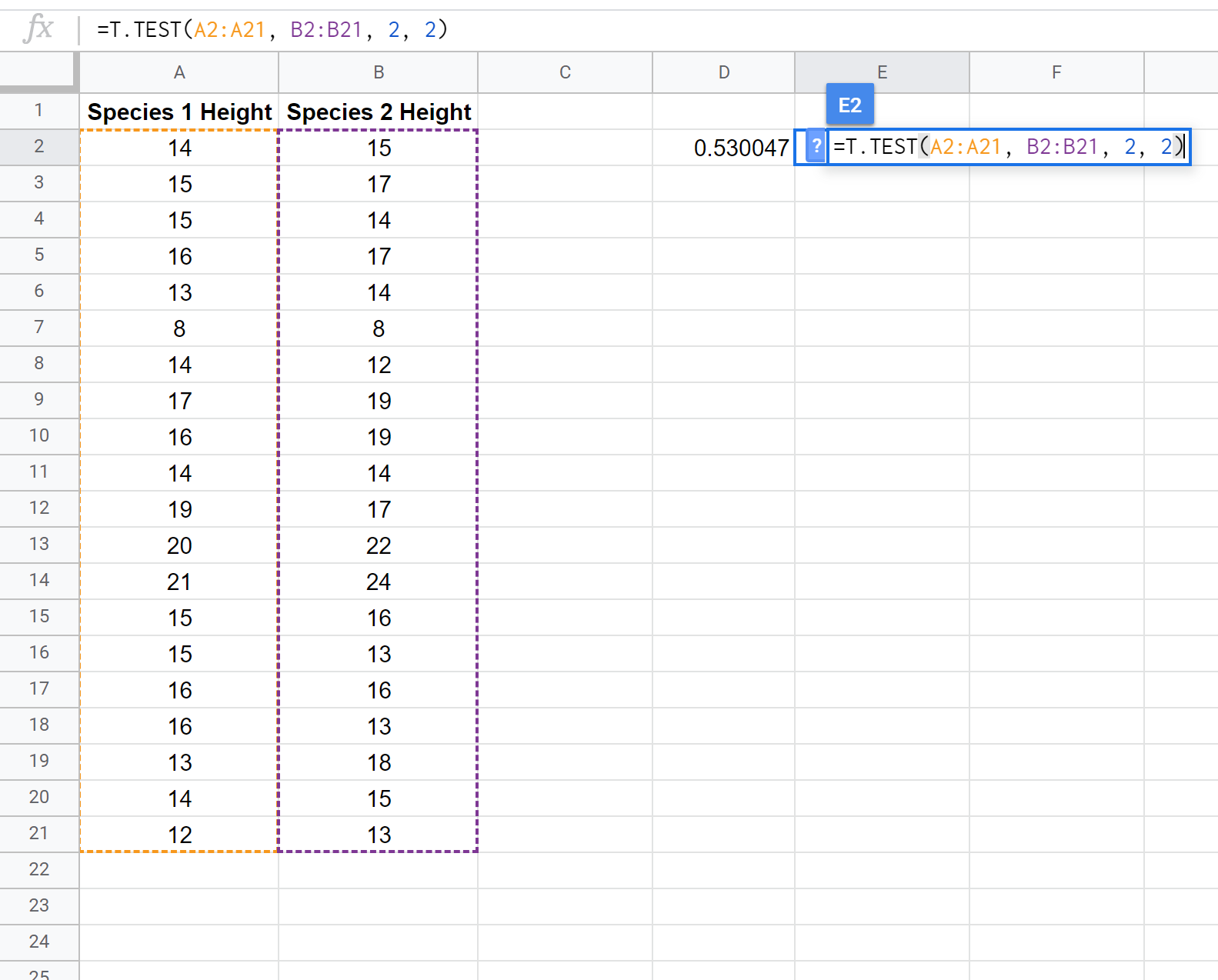
ملاحظة: من الممكن أيضًا إجراء اختبار t أحادي الطرف لعينتين مع أو بدون افتراض أن العينتين لهما نفس التباين. راجع وثائق T.TEST لمعرفة كيفية ضبط افتراضات الاختبار.

الفرضيتين لهذا الاختبار t المكون من عينتين هما:

H ₀ : μ ₁ = μ ₂ (متوسطا السكان متساويان)

H ₁ : μ ₁ ≠ μ ₂ (وسطا السكان غير متساويين)

نظرًا لأن القيمة p للاختبار (0.530047) أكبر من alpha = 0.05، فإننا نفشل في رفض الفرضية الصفرية للاختبار. ليس لدينا أدلة كافية لنقول أن متوسط ارتفاع هذا النوع بالذات من النباتات هو أكثر من 15 بوصة.

مثال: اختبار t للعينات المقترنة

التعريف: يتم استخدام اختبار t للعينات المقترنة لمقارنة متوسطي عينتين عندما يمكن ربط كل ملاحظة من عينة واحدة بملاحظة من العينة الأخرى.

مثال: نريد أن نعرف ما إذا كان المقرر الدراسي له تأثير كبير على أداء الطلاب في اختبار معين. ولاختبار ذلك، طلبنا من 20 طالبًا في الفصل إجراء اختبار مسبق. ثم نجعل كل طالب يشارك في المنهج لمدة أسبوعين. ثم يقوم الطلاب بإعادة إجراء اختبار بنفس الصعوبة.

توضح لقطة الشاشة التالية كيفية إجراء اختبار t لعينة مقترنة لمقارنة الفرق بين متوسط درجات الاختبارين الأول والثاني:

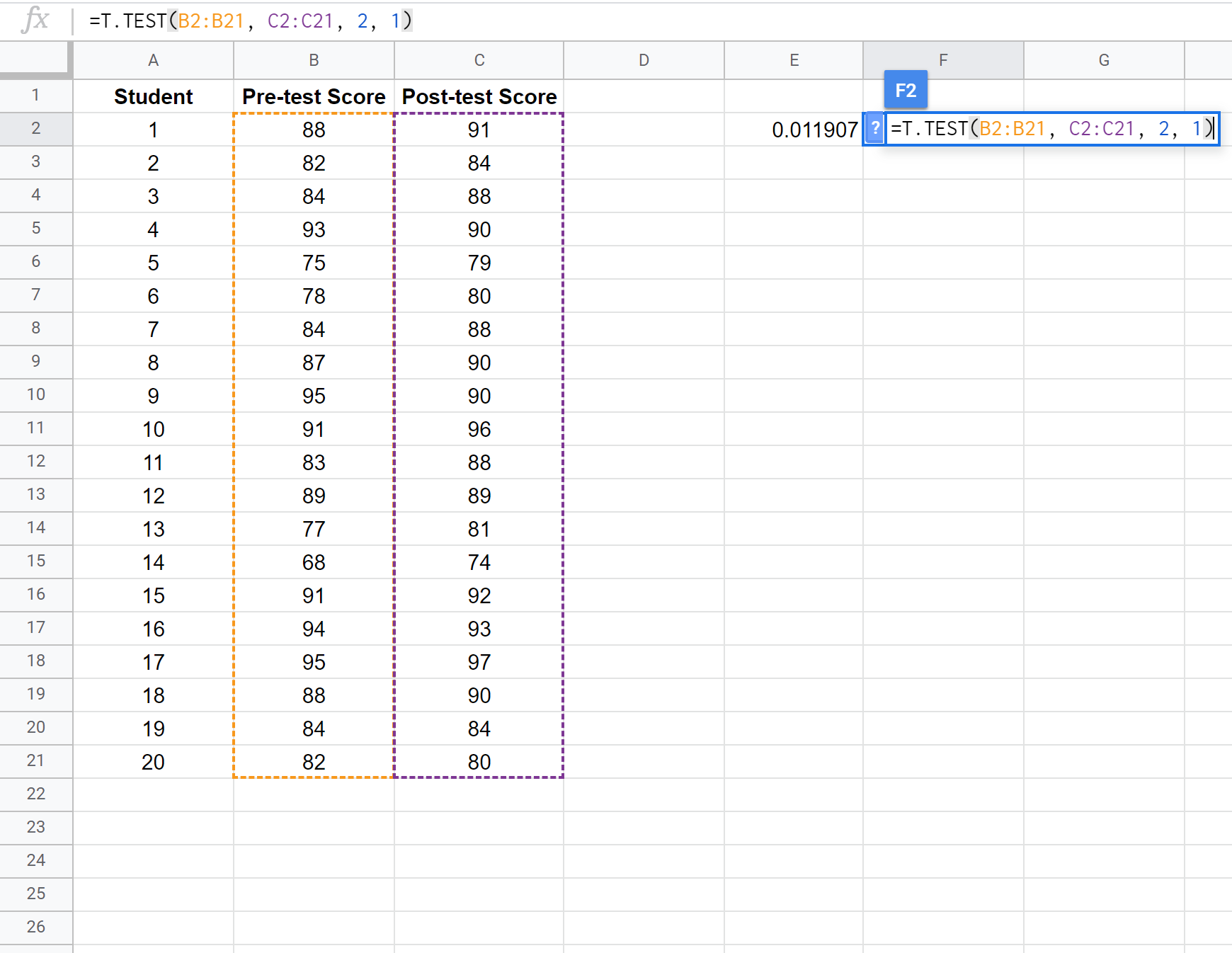
ملاحظة: من الممكن أيضًا إجراء اختبار t أحادي الطرف لعينتين مع أو بدون افتراض أن العينتين لهما نفس التباين. راجع وثائق T.TEST لمعرفة كيفية ضبط افتراضات الاختبار.

الافتراضان لهذا الاختبار t للعينات المقترنة هما:

H ₀ : μ ₁ = μ ₂ (متوسطا السكان متساويان)

H ₁ : μ ₁ ≠ μ ₂ (وسطا السكان غير متساويين)

نظرًا لأن القيمة p للاختبار (0.011907) أقل من alpha = 0.05، فإننا نرفض الفرضية الصفرية للاختبار. لدينا ما يكفي من الأدلة لنقول أن هناك فرق ذو دلالة إحصائية بين متوسط درجات الاختبار القبلي والبعدي.