كيفية إجراء اختبار t مع أحجام عينة غير متساوية

السؤال الذي يطرحه الطلاب غالبًا عندما يتعلق الأمر بالإحصاءات هو:

هل من الممكن إجراء اختبار t عندما تكون أحجام العينات في كل مجموعة غير متساوية؟

الجواب القصير:

نعم، يمكنك إجراء اختبار t عندما تكون أحجام العينات غير متساوية. لا تعد أحجام العينات المتساوية أحد الافتراضات الواردة في اختبار t.

تنشأ المشاكل الحقيقية عندما لا يكون للعينتين تباينات متساوية، وهو أحد الافتراضات التي يتم وضعها في اختبار t.

عندما يحدث هذا، فمن المستحسن استخدام اختبار ويلش بدلاً من ذلك، والذي لا يفترض تباينات متساوية.

توضح الأمثلة التالية كيفية إجراء اختبارات T بأحجام عينات غير متساوية عندما تكون التباينات متساوية وعندما لا تكون كذلك.

مثال 1: أحجام العينات غير المتكافئة والتباينات المتساوية

لنفترض أننا ندير برنامجين مصممين لمساعدة الطلاب على الأداء بشكل أفضل في اختبارات معينة.

النتائج كما يلي:

البرنامج 1:

• ن (حجم العينة): 500
• س (متوسط العينة): 80
• ق (عينة الانحراف المعياري): 5

البرنامج 2:

• ن (حجم العينة): 20
• س (متوسط العينة): 85
• ق (عينة الانحراف المعياري): 5

يوضح الكود التالي كيفية إنشاء boxplot في R لتصور توزيع درجات الاختبار لكل برنامج:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

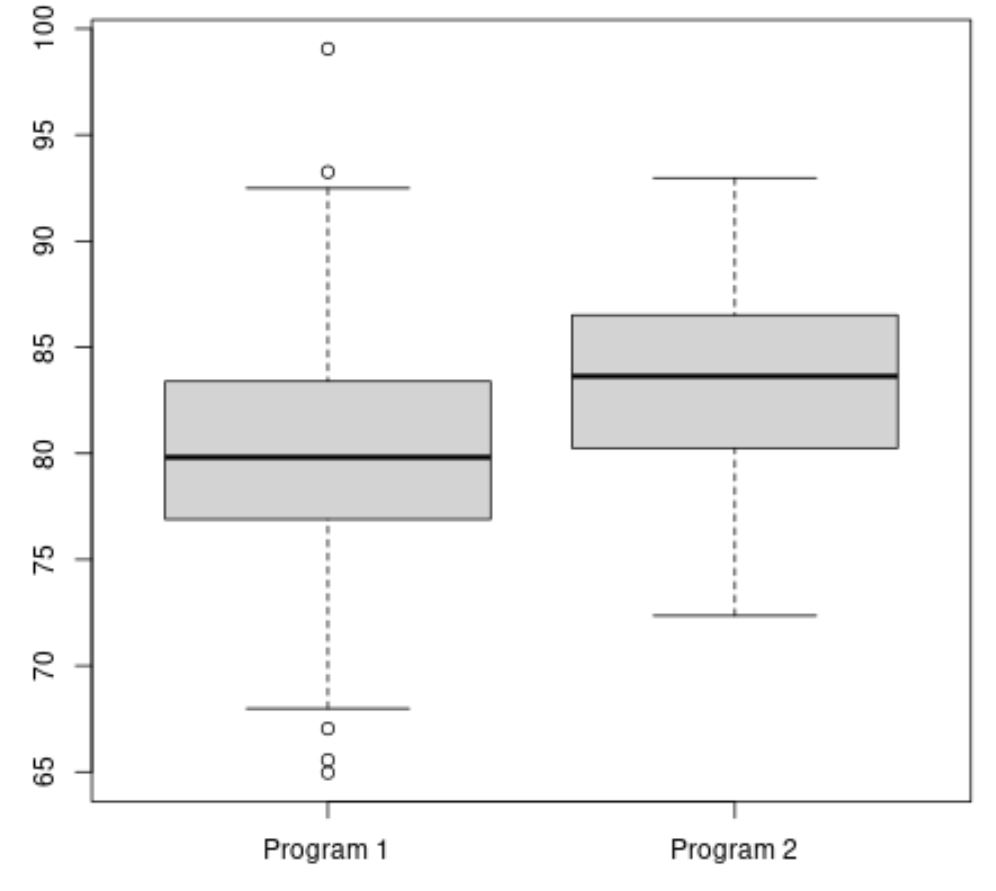
يبدو أن متوسط درجات الاختبار للبرنامج 2 أعلى، لكن التباين في درجات الاختبار بين البرنامجين متساوي تقريبًا.

يوضح التعليمة البرمجية التالية كيفية إجراء اختبار t للعينات المستقلة باستخدام اختبار Welch’s t:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

يُرجع اختبار t للعينات المستقلة قيمة p تبلغ 0.0009 ويعيد اختبار Welch’s t قيمة p تبلغ 0.0029 .

وبما أن القيمة p لكل اختبار أقل من 0.05، فإننا نرفض فرضية العدم في كل اختبار ونستنتج أن هناك فرقًا ذا دلالة إحصائية في متوسط درجات الاختبار بين البرنامجين.

على الرغم من أن أحجام العينات غير متساوية، فإن اختبار t للعينات المستقلة واختبار t لـ Welch يُرجعان نتائج مماثلة نظرًا لأن العينتين لهما تباينات متساوية.

مثال 2: أحجام العينات غير المتكافئة والتباينات غير المتكافئة

لنفترض أننا ندير برنامجين مصممين لمساعدة الطلاب على الأداء بشكل أفضل في اختبارات معينة.

النتائج كما يلي:

البرنامج 1:

• ن (حجم العينة): 500
• س (متوسط العينة): 80
• ق (عينة الانحراف المعياري): 25

البرنامج 2:

• ن (حجم العينة): 20
• س (متوسط العينة): 85
• ق (عينة الانحراف المعياري): 5

يوضح الكود التالي كيفية إنشاء boxplot في R لتصور توزيع درجات الاختبار لكل برنامج:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

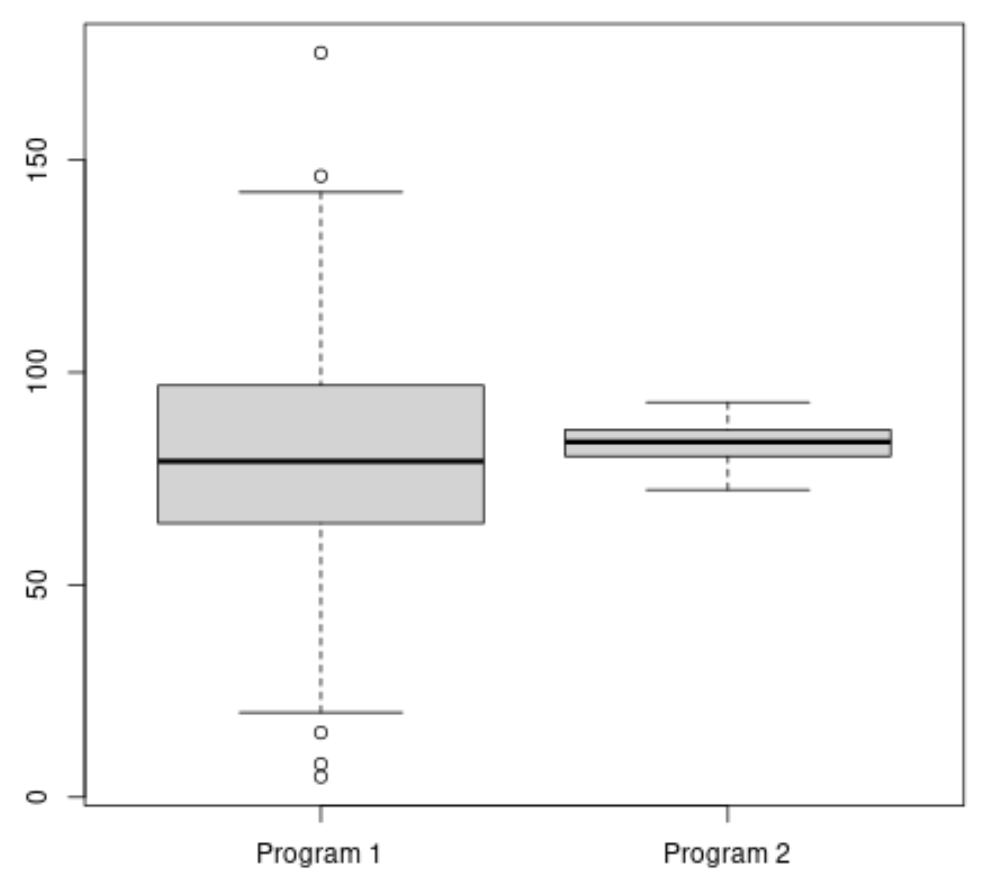
يبدو أن متوسط درجات الاختبار للبرنامج 2 أعلى، لكن التباين في درجات الاختبار للبرنامج 1 أعلى بكثير من ذلك الخاص بالبرنامج 2.

يوضح التعليمة البرمجية التالية كيفية إجراء اختبار t للعينات المستقلة باستخدام اختبار Welch’s t:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

يُرجع اختبار t للعينات المستقلة قيمة p تبلغ 0.5496 ويعيد اختبار Welch’s t قيمة p تبلغ 0.0361 .

لا يستطيع اختبار t للعينات المستقلة اكتشاف الفرق في متوسط درجات الامتحانات، لكن اختبار Welch’s t قادر على اكتشاف فرق ذي دلالة إحصائية.

وبما أن العينتين كانت لهما تباينات غير متساوية، فإن اختبار ويلش فقط هو الذي كان قادرًا على اكتشاف الفرق ذو دلالة إحصائية في متوسط درجات الامتحان، حيث أن هذا الاختبار لا يفترض تباينات متساوية بين العينات .

مصادر إضافية

توفر البرامج التعليمية التالية معلومات إضافية حول اختبارات t:

مقدمة لاختبار t للعينة الواحدة
مقدمة لاختبار t ذو العينتين
مقدمة لاختبار t للعينات المقترنة