كيفية إجراء اختبار دونيت في r

الاختبار اللاحق هو نوع من الاختبارات التي يتم إجراؤها بعد تحليل التباين (ANOVA) لتحديد متوسطات المجموعة التي تختلف بشكل كبير إحصائيًا عن بعضها البعض.

إذا كانت إحدى مجموعات الدراسة تعتبر المجموعة الضابطة ، فيجب علينا استخدام اختبار دونيت كاختبار ما بعد مخصص.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار Dunnett في R.

مثال: اختبار دونيت في R

لنفترض أن أحد المعلمين يريد معرفة ما إذا كانت هناك طريقتان دراسيتان جديدتان لديهما القدرة على تحسين درجات اختبار طلابها. ولاختبار ذلك، قامت بتقسيم فصلها المكون من 30 طالبًا بشكل عشوائي إلى المجموعات الثلاث التالية:

• المجموعة الضابطة: 10 طلاب
• الدراسة الفنية الجديدة 1: 10 طلاب
• الدراسة الفنية الجديدة 2: 10 طلاب

وبعد أسبوع من استخدام أسلوب الدراسة المخصص لهم، يقوم كل طالب بإجراء نفس الاختبار.

يمكننا استخدام الخطوات التالية في لغة R لإنشاء مجموعة بيانات، وتصور وسائل المجموعة، وإجراء تحليل التباين (ANOVA) أحادي الاتجاه، وأخيرًا إجراء اختبار دونيت لتحديد تقنية الدراسة الجديدة (إن وجدت) التي تنتج نتائج مختلفة مقارنةً بالمجموعة الضابطة. .

الخطوة 1: إنشاء مجموعة البيانات.

يوضح الكود التالي كيفية إنشاء مجموعة بيانات تحتوي على نتائج الامتحانات لجميع الطلاب الثلاثين:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

الخطوة الثانية: عرض نتائج الامتحانات لكل مجموعة.

يوضح الكود التالي كيفية إنتاج boxplots لتصور توزيع نتائج الاختبار لكل مجموعة:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

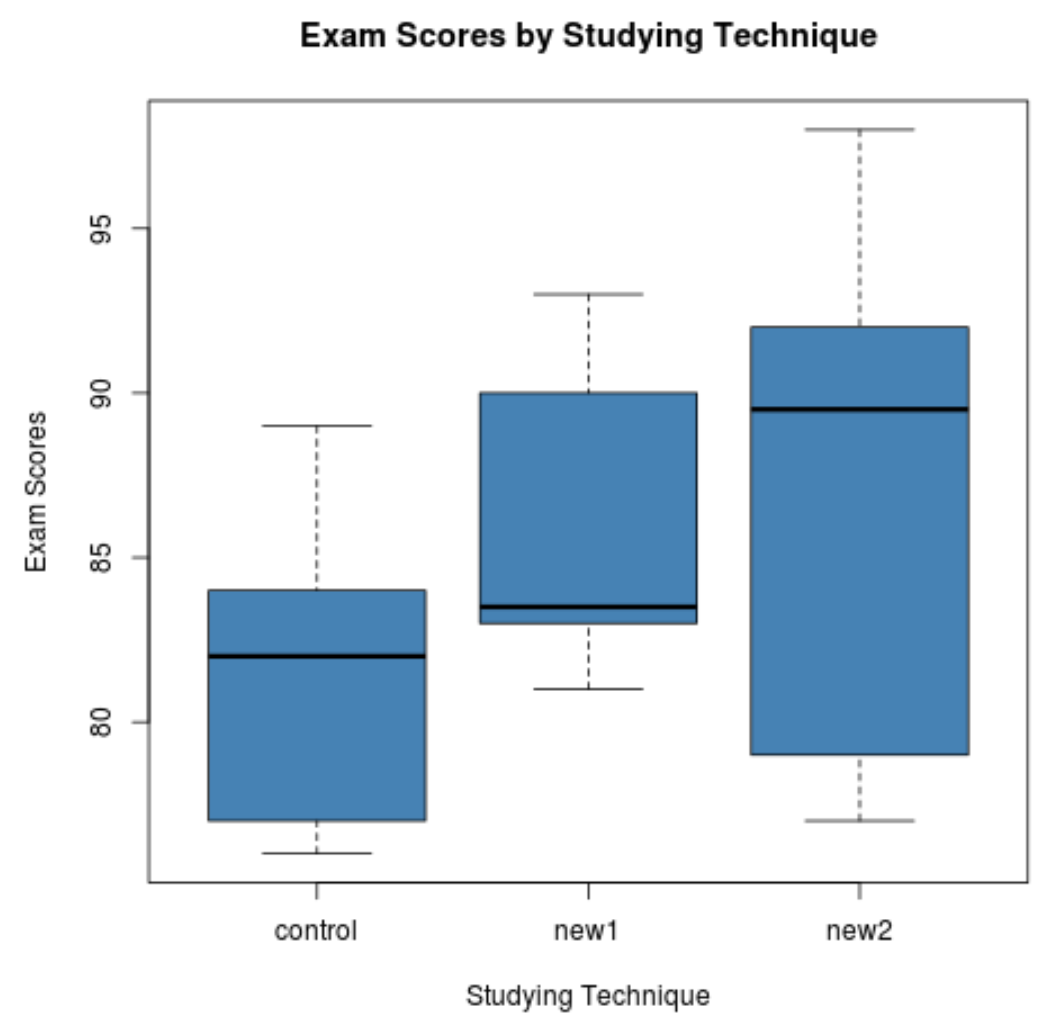
فقط من المخططات المربعة، يمكننا أن نرى أن توزيع درجات الامتحانات يختلف تمامًا لكل أسلوب دراسة. سنقوم بعد ذلك بإجراء تحليل التباين (ANOVA) أحادي الاتجاه لتحديد ما إذا كانت هذه الاختلافات ذات دلالة إحصائية.

ذات صلة: كيفية رسم مخططات مربعة متعددة في مخطط واحد في R

الخطوة 3: إجراء تحليل التباين (ANOVA) في اتجاه واحد.

يوضح الكود التالي كيفية إجراء تحليل التباين (ANOVA) أحادي الاتجاه لاختبار الاختلافات بين متوسط درجات الاختبار في كل مجموعة:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

وبما أن القيمة الاحتمالية الإجمالية ( 0.0476 ) أقل من 0.05، فهذا يشير إلى أن كل مجموعة ليس لديها نفس متوسط درجات الاختبار. بعد ذلك، سنقوم بإجراء اختبار دونيت لتحديد أسلوب الدراسة الذي ينتج متوسط درجات الامتحانات التي تختلف عن تلك الخاصة بالمجموعة الضابطة.

الخطوة 4: إجراء اختبار دونيت.

لإجراء اختبار Dunnett في R يمكننا استخدام وظيفة DunnettTest() من مكتبة DescTools التي تستخدم الصيغة التالية:

اختبار دونيت (س، ز)

ذهب:

• x: متجه رقمي لقيم البيانات (مثل نتائج الامتحانات)
• g: متجه يحدد أسماء المجموعات (مثل تقنية الدراسة)

يوضح الكود التالي كيفية استخدام هذه الوظيفة لمثالنا:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

وطريقة تفسير النتيجة هي كما يلي:

• متوسط الفرق في درجات الامتحان بين أسلوب الدراسة الجديد 1 والمجموعة الضابطة هو 4.2. القيمة p المقابلة هي 0.1787 .
• متوسط الفرق في درجات الامتحان بين أسلوب الدراسة الجديد 2 والمجموعة الضابطة هو 6.4. القيمة p المقابلة هي 0.0296 .

وبناء على النتائج، يمكننا أن نرى أن دراسة التقنية الثانية هي التقنية الوحيدة التي تنتج متوسط درجات الامتحانات التي تختلف بشكل كبير (ع = 0.0296) عن تلك الخاصة بالمجموعة الضابطة.

مصادر إضافية

مقدمة إلى تحليل التباين الأحادي (One-Way ANOVA).
كيفية إجراء ANOVA أحادي الاتجاه في R
كيفية إجراء اختبار توكي في R