كيفية إجراء اختبار وايت في sas

يتم استخدام اختبار وايت لتحديد ما إذا كانت التغايرية موجودة في نموذج الانحدار.

تشير التغايرية إلى التشتت غير المتساوي للبقايا على مستويات مختلفة لمتغير الاستجابة في نموذج الانحدار، وهو ما ينتهك أحد الافتراضات الرئيسية للانحدار الخطي المتمثل في أن البقايا منتشرة بالتساوي على كل مستوى من متغير الاستجابة.

يشرح هذا البرنامج التعليمي كيفية إجراء الاختبار الأبيض في SAS لتحديد ما إذا كانت التغايرية تمثل مشكلة في نموذج انحدار معين أم لا.

مثال: الاختبار الأبيض في SAS

لنفترض أننا نريد ملاءمة نموذج الانحدار الخطي المتعدد الذي يستخدم عدد الساعات التي يقضيها في الدراسة وعدد اختبارات التدريب التي تم إجراؤها للتنبؤ بدرجة الاختبار النهائي للطلاب:

درجة الامتحان = β ₀ + β ₁ (ساعات) + β ₂ (الاختبارات التحضيرية)

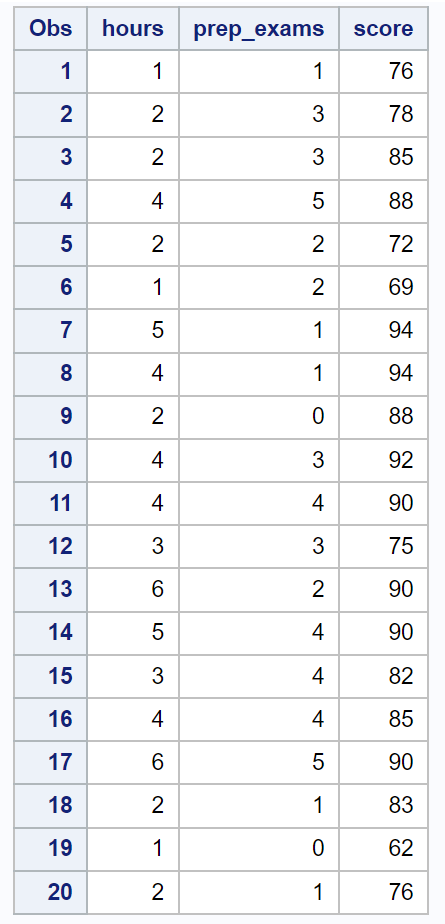
أولاً، سنستخدم الكود التالي لإنشاء مجموعة بيانات تحتوي على هذه المعلومات لـ 20 طالبًا:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

بعد ذلك، سوف نستخدم proc reg لملاءمة نموذج الانحدار الخطي المتعدد هذا بالإضافة إلى خيار المواصفات لإجراء اختبار White للتغايرية:

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

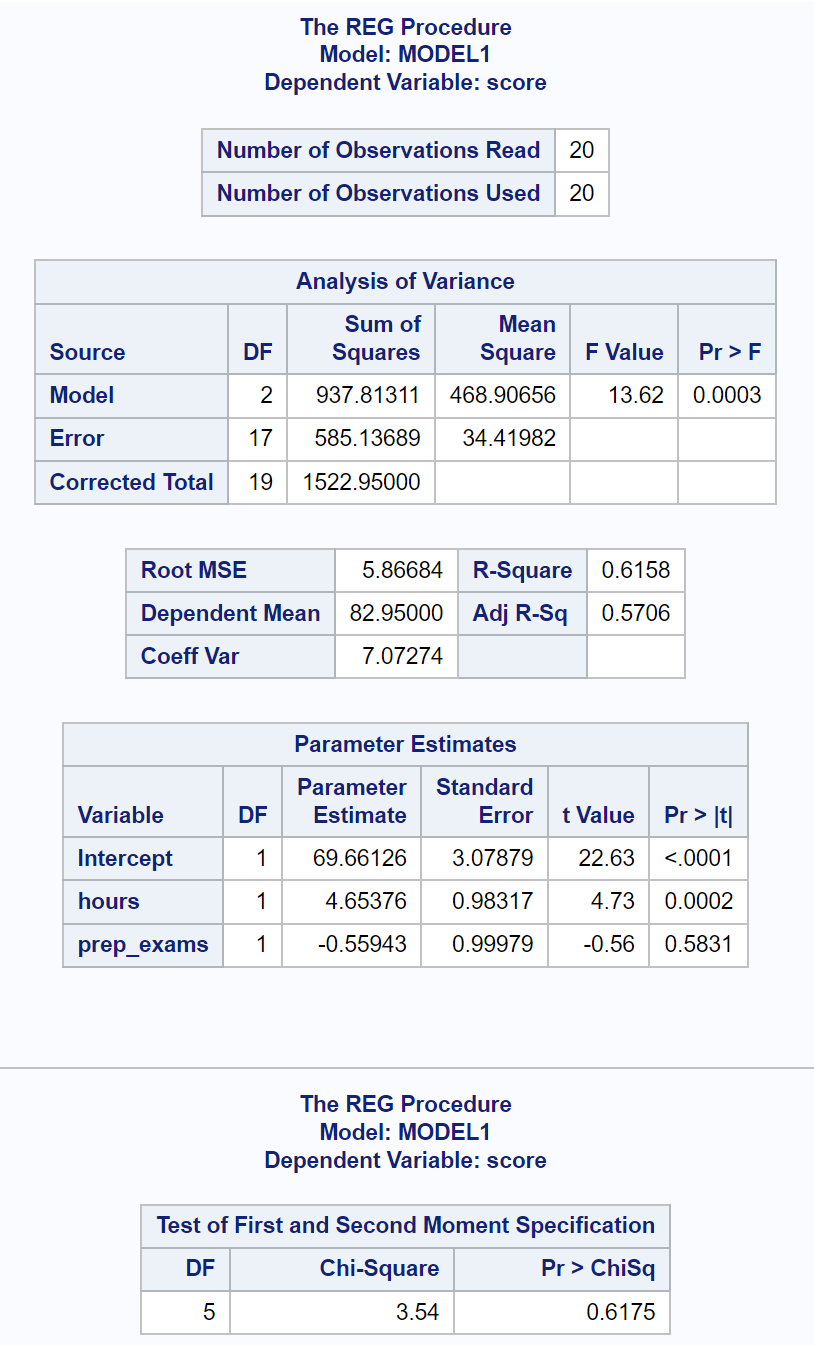
ويبين جدول النتائج الأخير نتائج اختبار وايت.

من هذا الجدول، يمكننا أن نرى أن إحصائيات اختبار مربع كاي هي 3.54 والقيمة الاحتمالية المقابلة هي 0.6175 .

يستخدم الاختبار الأبيض الفرضيات الصفرية والبديلة التالية:

• Null (H ₀ ) : التغاير غير موجود.
• البديل ( _HA ): التغايرية موجودة.

وبما أن القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم.

وهذا يعني أنه ليس لدينا أدلة كافية للادعاء بوجود عدم تجانس في نموذج الانحدار.

لذلك من الممكن تفسير الأخطاء المعيارية لتقديرات المعامل بأمان في جدول ملخص الانحدار.

ما العمل التالي

إذا فشلت في رفض الفرضية الصفرية لاختبار وايت، فإن التغايرية غير موجودة ويمكنك المتابعة لتفسير نتيجة الانحدار الأصلي.

ومع ذلك، إذا رفضت فرضية العدم، فهذا يعني أن التغايرية موجودة في البيانات. في هذه الحالة، قد تكون الأخطاء القياسية المعروضة في جدول مخرجات الانحدار غير موثوقة.

هناك عدة طرق شائعة لحل هذه المشكلة، بما في ذلك:

1. تحويل متغير الاستجابة. يمكنك محاولة إجراء تحويل على متغير الاستجابة.

على سبيل المثال، يمكنك استخدام متغير استجابة السجل بدلاً من متغير الاستجابة الأصلي.

بشكل عام ، يعد أخذ سجل متغير الاستجابة طريقة فعالة لإخفاء عدم التجانس.

التحويل الشائع الآخر هو استخدام الجذر التربيعي لمتغير الاستجابة.

2. استخدم الانحدار المرجح. يقوم هذا النوع من الانحدار بتعيين وزن لكل نقطة بيانات بناءً على تباين قيمتها المجهزة.

وهذا يعطي أوزانًا صغيرة لنقاط البيانات التي تحتوي على تباينات أعلى، مما يقلل من مربعاتها المتبقية.

عند استخدام الأوزان المناسبة، يمكن أن يؤدي ذلك إلى القضاء على مشكلة عدم التجانس.