كيفية إجراء اختبار فريدمان في spss

اختبار فريدمان هو بديل غير معلمي للقياسات المتكررة ANOVA . يتم استخدامه لتحديد ما إذا كان هناك فرق ذو دلالة إحصائية بين متوسطات ثلاث مجموعات أو أكثر تظهر فيها نفس المواضيع في كل مجموعة أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار فريدمان في برنامج SPSS.

مثال: اختبار فريدمان في برنامج SPSS

يريد الباحثون معرفة ما إذا كانت أربعة أدوية مختلفة تسبب أوقات رد فعل مختلفة. ولاختبار ذلك، قاموا بقياس أوقات رد فعل خمسة مرضى لأربعة أدوية مختلفة.

أكمل الخطوات التالية لإجراء اختبار فريدمان في برنامج SPSS لتحديد ما إذا كان وقت التفاعل يختلف بين الأدوية.

الخطوة 1: أدخل البيانات.

أدخل البيانات التالية التي توضح زمن الاستجابة (بالثواني) لخمسة مرضى للأدوية الأربعة:

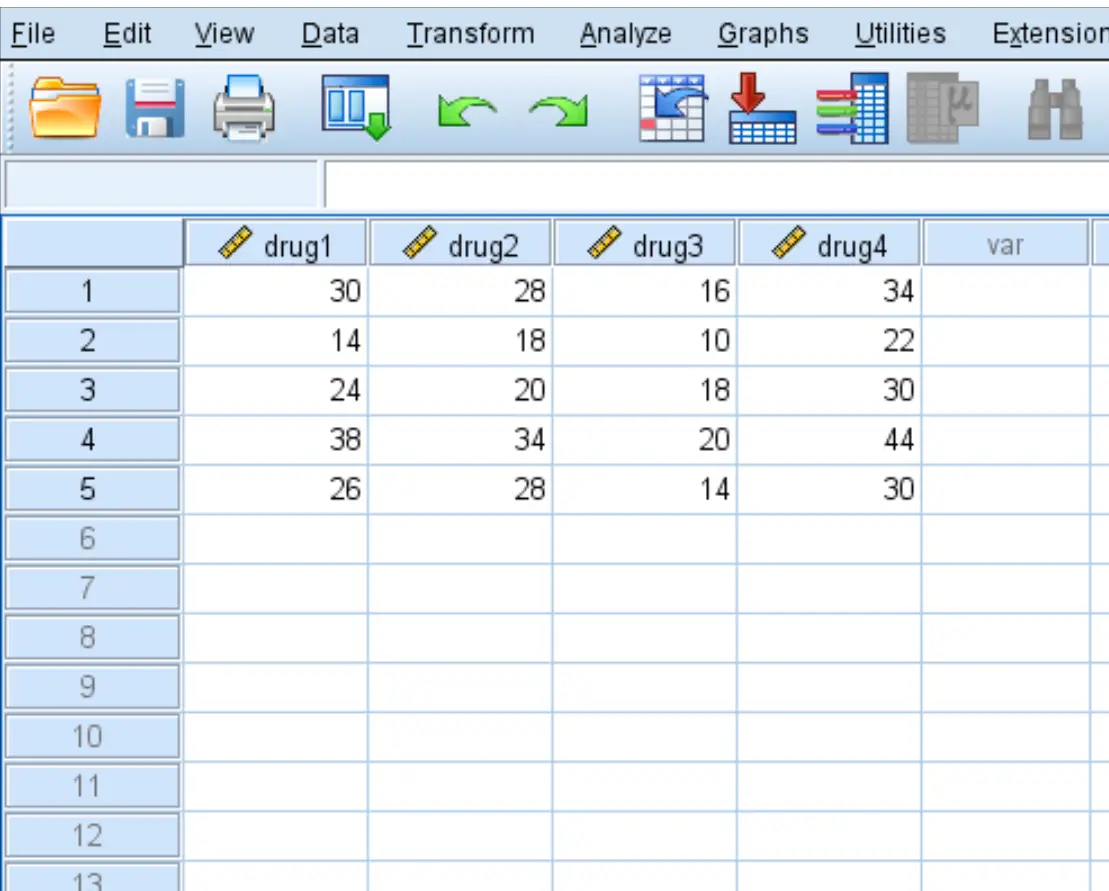
الخطوة الثانية: إجراء اختبار فريدمان.

انقر فوق علامة التبويب تحليل ، ثم الاختبارات اللامعلمية ، ثم مربعات الحوار القديمة ، ثم عينات K ذات الصلة .

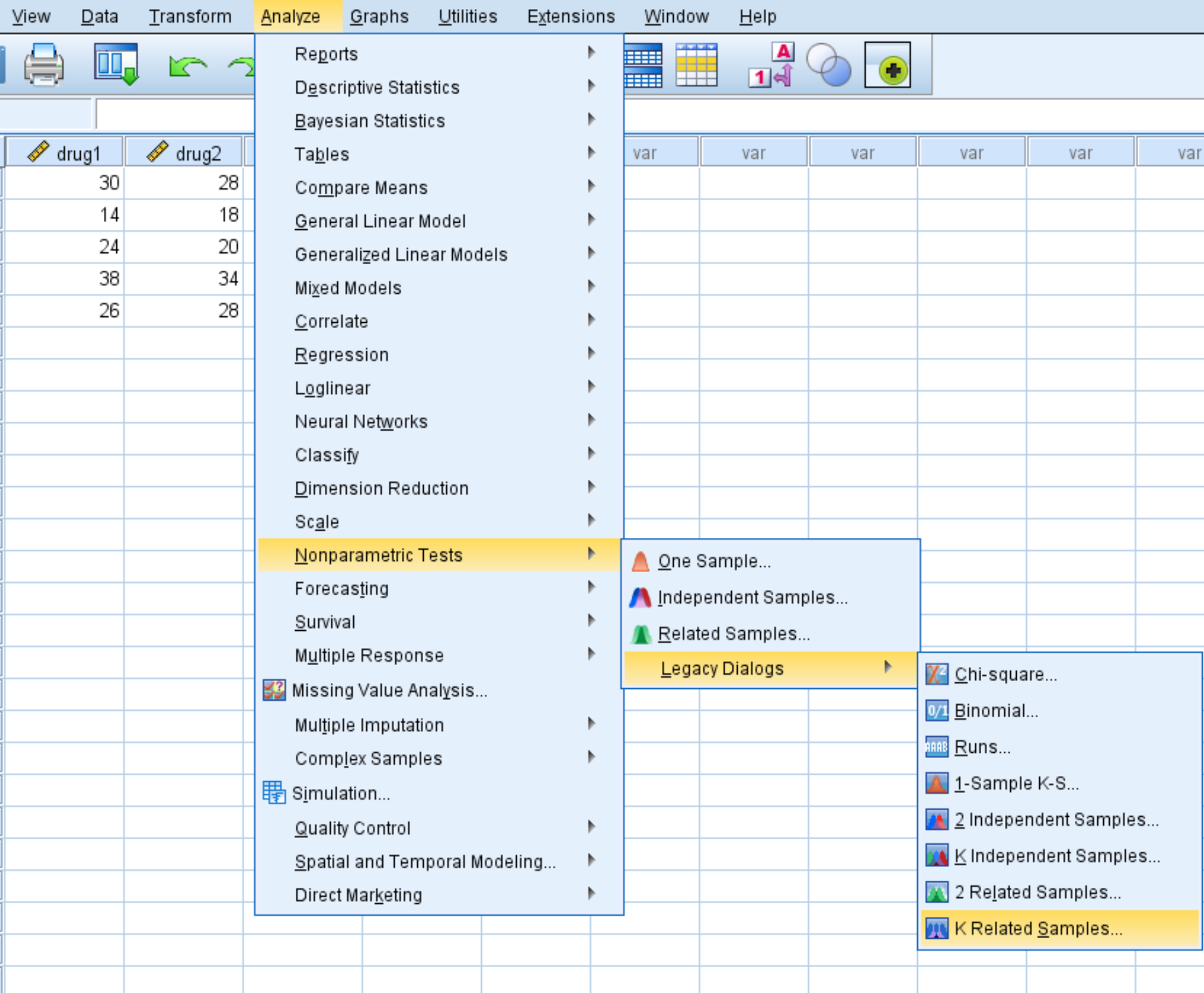
في النافذة الجديدة التي تظهر، اسحب متغيرات الدواء الأربعة إلى المنطقة المسماة “متغيرات الاختبار” . تأكد من تحديد المربع المجاور لـ Friedman ، ثم انقر فوق OK (موافق) .

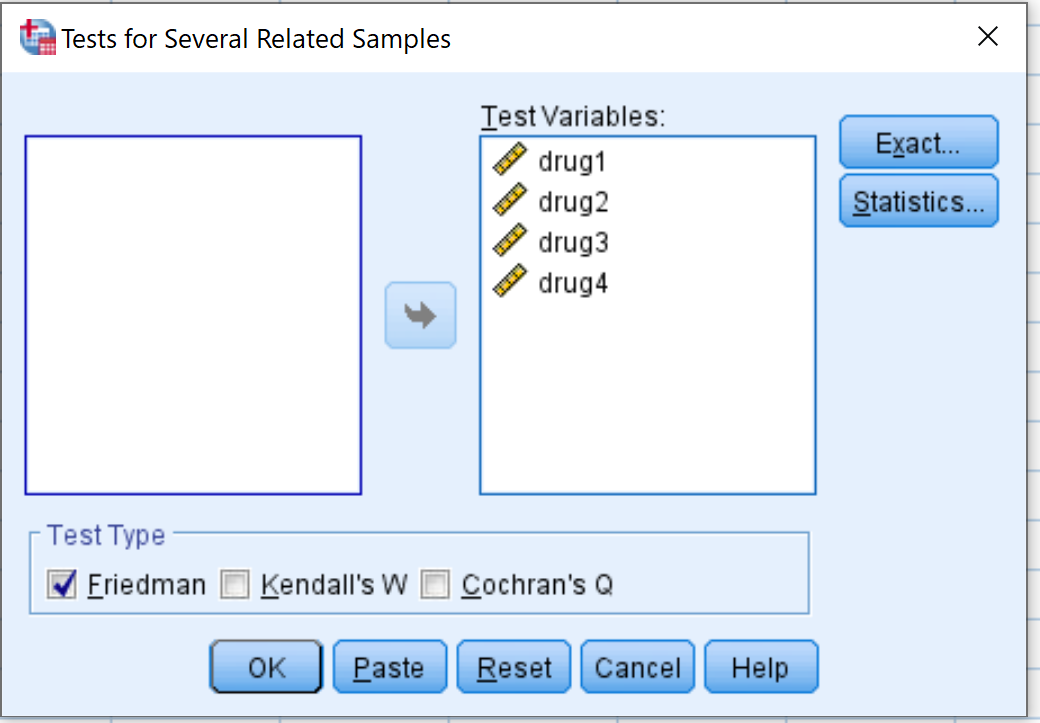
الخطوة 3: تفسير النتائج.

بمجرد الضغط على موافق ، ستظهر نتائج اختبار فريدمان:

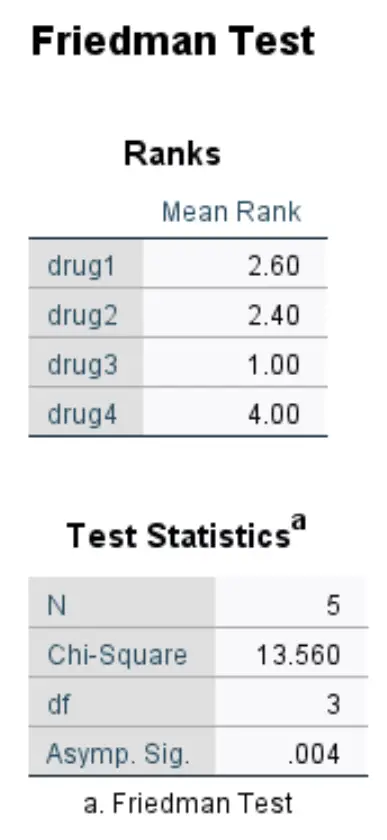
وإليك كيفية تفسير النتيجة:

N: العدد الإجمالي للأفراد في مجموعة البيانات.

مربع تشي: إحصائية اختبار فريدمان.

df: درجات الحرية، ويتم حسابها على النحو التالي: #groups-1 = 4-1 = 3.

أسيمب. Sig: القيمة p المرتبطة بإحصائيات الاختبار بثلاث درجات حرية. في هذه الحالة، القيمة p هي 0.004 . ويمكن أيضًا حساب ذلك باستخدام حاسبة قيمة مربع كاي إلى حاسبة القيمة P.

وبما أن القيمة p أقل من 0.05، يمكننا رفض فرضية العدم القائلة بأن زمن الاستجابة هو نفسه لجميع الأدوية الأربعة. لدينا ما يكفي من الأدلة لنستنتج أن نوع الدواء المستخدم يؤدي إلى اختلافات ذات دلالة إحصائية في وقت الاستجابة.

الخطوة 4: الإبلاغ عن النتائج.

وأخيرا، نود أن نعلن عن نتائج الاختبار. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء اختبار فريدمان على خمسة أفراد لفحص تأثير أربعة أدوية مختلفة على زمن الاستجابة. كل فرد يستخدم كل دواء مرة واحدة.

أظهرت النتائج أن نوع الدواء المستخدم أدى إلى فروق ذات دلالة إحصائية في زمن الاستجابة (X ² = 13.56، p = 0.004).