ما هو اختبار كوكران q؟ (التعريف & #038؛ مثال)

اختبار كوكران Q هو اختبار إحصائي يستخدم لتحديد ما إذا كانت نسبة “النجاحات” متساوية في ثلاث مجموعات أو أكثر يظهر فيها نفس الأفراد في كل مجموعة.

على سبيل المثال، يمكننا استخدام اختبار كوكران Q لتحديد ما إذا كانت نسبة الطلاب الذين اجتازوا الاختبار متساوية عند استخدام ثلاث تقنيات دراسية مختلفة.

خطوات إجراء اختبار كوكران Q

يستخدم اختبار كوكران Q الفرضيات الصفرية والبديلة التالية:

الفرضية الصفرية ( _H0 ): نسبة “النجاحات” هي نفسها في جميع المجموعات

الفرضية البديلة ( _HA ): تختلف نسبة “النجاحات” في إحدى المجموعات على الأقل

يتم حساب إحصائية الاختبار على النحو التالي:

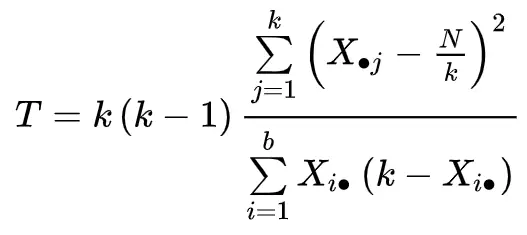
ذهب:

• ك: عدد العلاجات (أو “المجموعات”)
• Xj: إجمالي العمود الخاص بالمعاملة ^j
• ب: عدد الكتل
• شي. : إجمالي السطر للكتلة ⁱ
• ن: المجموع الكلي

تتبع إحصائية اختبار T توزيع مربع كاي بدرجة حرية k-1 .

إذا كانت القيمة p المرتبطة بإحصائيات الاختبار أقل من مستوى معين من الأهمية (مثل α = 0.05)، فيمكننا رفض فرضية العدم ونستنتج أن لدينا أدلة كافية لنقول أن نسبة “النجاحات” مختلفة في واحدة على الأقل من المجموعات.

مثال: اختبار كوكران Q

لنفترض أن أحد الباحثين يريد معرفة ما إذا كانت ثلاث تقنيات دراسة مختلفة تؤدي إلى نسب مختلفة من معدلات النجاح بين الطلاب.

ولاختبار ذلك، قامت بتجنيد 20 طالبًا يخضع كل منهم لامتحان متساوي الصعوبة باستخدام ثلاث تقنيات دراسية مختلفة. النتائج موضحة أدناه:

لإجراء اختبار Cochran’s Q، يمكننا استخدام البرامج الإحصائية لأنه قد يكون من الصعب إجراؤه يدويًا.

إليك الكود الذي يمكننا استخدامه لإنشاء مجموعة البيانات هذه وإجراء اختبار Cochran’s Q بلغة البرمجة الإحصائية R:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

ومن نتيجة الاختبار يمكننا ملاحظة ما يلي:

• إحصائيات الاختبار هي 0.333
• القيمة p المقابلة هي 0.8465

وبما أن هذه القيمة p لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم.

وهذا يعني أنه ليس لدينا أدلة كافية للقول بأن أسلوب الدراسة الذي يستخدمه الطلاب يؤدي إلى نسب مختلفة من معدلات النجاح.