اختبار مان ويتني يو
يتم استخدام اختبار مان ويتني يو (يسمى أحيانًا اختبار مجموع رتب ويلكوكسون) لمقارنة الاختلافات بين عينتين مستقلتين عندما لا يتم توزيع توزيعات العينة بشكل طبيعي وتكون أحجام العينة صغيرة (ن <30).
ويعتبر المعادل اللامعلمي لاختبار t المستقل المكون من عينتين .
فيما يلي بعض الأمثلة على الأوقات التي يمكنك فيها استخدام اختبار Mann-Whitney U:
- تريد مقارنة رواتب خمسة خريجين من الجامعة (أ) برواتب خمسة خريجين من الجامعة (ب). لا يتم توزيع الرواتب بشكل طبيعي.
- تريد معرفة ما إذا كان فقدان الوزن يختلف بين مجموعتين: 12 شخصًا يستخدمون النظام الغذائي “أ” و10 أشخاص يستخدمون النظام الغذائي “ب”. لا يتم توزيع فقدان الوزن بشكل طبيعي.
- تريد معرفة ما إذا كانت درجات 8 طلاب في الفصل “أ” تختلف عن درجات 7 طلاب في الفصل “ب”. لا يتم توزيع الدرجات بشكل طبيعي.
في كل مثال، تريد مقارنة مجموعتين، وتوزيعات العينات ليست طبيعية، وأحجام العينات صغيرة.
وبالتالي، فإن اختبار مان ويتني يو يكون مناسبًا طالما تم استيفاء الافتراضات التالية.
افتراضات اختبار مان ويتني يو
قبل إجراء اختبار مان ويتني يو، يجب عليك التأكد من استيفاء الافتراضات الأربعة التالية:
- عادي أو مستمر: المتغير الذي تقوم بتحليله هو ترتيبي أو مستمر. تتضمن أمثلة المتغيرات الترتيبية عناصر ليكرت (على سبيل المثال، مقياس مكون من 5 نقاط يتراوح من “لا أوافق بشدة” إلى “أوافق بشدة”). تتضمن أمثلة المتغيرات المستمرة الارتفاع (مقاسًا بالبوصة)، أو الوزن (مقاسًا بالجنيه)، أو درجات الاختبار (مقاسًا من 0 إلى 100).
- الاستقلال: جميع الملاحظات من كلا المجموعتين مستقلة عن بعضها البعض.
- الشكل: أشكال التوزيعات للمجموعتين متماثلة تقريبًا.
إذا تم استيفاء هذه الافتراضات، فيمكنك إجراء اختبار مان ويتني يو.
كيفية إجراء اختبار مان ويتني يو
لإجراء اختبار مان ويتني يو، نتبع الإجراء القياسي لاختبار الفرضيات المكون من خمس خطوات :
1. اذكر الافتراضات.
في معظم الحالات، يتم إجراء اختبار مان ويتني يو كاختبار ثنائي الذيل. وتكتب الفرضيات الصفرية والبديلة بالصيغة التالية:
H 0 : المجموعتان متساويتان
ح أ : المجموعتان السكانيتان غير متساويتين
2. تحديد مستوى الأهمية لاستخدامه في الفرضية.
اتخاذ قرار بشأن مستوى الأهمية. الاختيارات الشائعة هي .01 و.05 و.1.
3. ابحث عن إحصائية الاختبار.
يُشار إلى إحصائية الاختبار بالرمز U وهي الأصغر من U 1 وU 2 ، كما هو محدد أدناه:
يو 1 = ن 1 ن 2 + ن 1 (ن 1 +1)/2 – ر 1
يو 2 = ن 1 ن 2 + ن 2 (ن 2 +1)/2 – ر 2
حيث n 1 وn 2 هما حجما العينة للعينتين 1 و2 على التوالي، وR 1 وR 2 هما مجموع رتب العينات 1 و2 على التوالي.
ستوضح الأمثلة أدناه كيفية العثور على إحصائية الاختبار هذه بالتفصيل.
4. ارفض أو لا ترفض الفرضية الصفرية.
باستخدام إحصائيات الاختبار، حدد ما إذا كان يمكنك رفض الفرضية الصفرية أم لا بناءً على مستوى الأهمية والقيمة الحرجة الموجودة في جدول Mann-Whitney U.
5. تفسير النتائج.
تفسير نتائج الاختبار في سياق السؤال المطروح.
أمثلة على إجراء اختبار مان ويتني يو
توضح الأمثلة التالية كيفية إجراء اختبار Mann-Whitney U.
مثال 1
نريد أن نعرف ما إذا كان الدواء الجديد فعالاً في الوقاية من نوبات الهلع أم لا. تم تقسيم إجمالي 12 مريضًا بشكل عشوائي إلى مجموعتين من 6 مرضى وتم تعيينهم لتلقي الدواء الجديد أو الدواء الوهمي. ثم يقوم المرضى بتسجيل عدد نوبات الهلع التي تعرضوا لها على مدار الشهر.
النتائج موضحة أدناه:
| دواء جديد | الوهمي |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
قم بإجراء اختبار Mann-Whitney U لمعرفة ما إذا كان هناك اختلاف في عدد نوبات الهلع بين المرضى في مجموعة الدواء الوهمي مقارنة بمجموعة الدواء الجديدة. استخدم مستوى أهمية 0.05.
1. اذكر الافتراضات.
H 0 : المجموعتان متساويتان
ح أ : المجموعتان السكانيتان غير متساويتين
2. تحديد مستوى الأهمية لاستخدامه في الفرضية.
تخبرنا المشكلة أنه يجب علينا استخدام مستوى أهمية قدره 0.05.
3. ابحث عن إحصائية الاختبار.
تذكَّر أن إحصائية الاختبار يُشار إليها بـ U وهي الأصغر بين U 1 وU 2 ، كما هو محدد أدناه:
يو 1 = ن 1 ن 2 + ن 1 (ن 1 +1)/2 – ر 1
يو 2 = ن 1 ن 2 + ن 2 (ن 2 +1)/2 – ر 2
حيث n 1 وn 2 هما حجما العينة للعينتين 1 و2 على التوالي، وR 1 وR 2 هما مجموع رتب العينات 1 و2 على التوالي.
من أجل العثور على R 1 و R 2 ، نحتاج إلى دمج الملاحظات من كلا المجموعتين وترتيبها من الأصغر إلى الأكبر:
| دواء جديد | الوهمي |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
العينة الإجمالية: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
الرتب: 1.5 ، 1.5 ، 3 ، 4.5 ، 4.5 ، 6.5 ، 6.5 ، 8.5 ، 8.5 ، 10 ، 11 ، 12
R 1 = مجموع الرتب للعينة 1 = 1.5+4.5+4.5+6.5+8.5+8.5 = 34
R 2 = مجموع الرتب للعينة 2 = 1.5+3+6.5+10+11+12 = 44
بعد ذلك، نستخدم أحجام العينات n 1 و n 2 بالإضافة إلى مجموع الرتب R 1 و R 2 للعثور على U 1 و U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
إحصائيات الاختبار لدينا هي الأصغر من U1 و U2 والتي تصادف أن تكون U=13.
ملاحظة: يمكننا أيضًا استخدام حاسبة اختبار Mann-Whitney U لتحديد أن U = 13.
4. ارفض أو لا ترفض الفرضية الصفرية.
باستخدام n 1 = 6 و n 2 = 6 بمستوى دلالة 0.05، يخبرنا جدول Mann-Whitney U أن القيمة الحرجة هي 5:
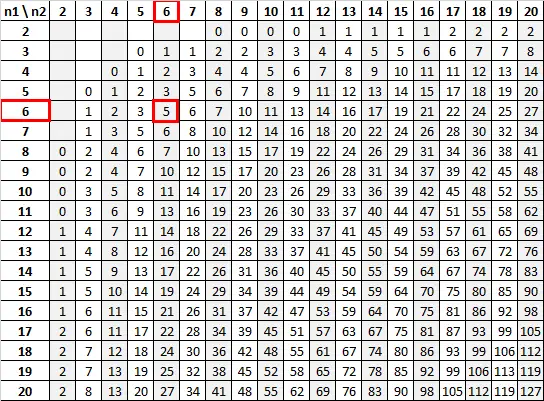
وبما أن إحصائية الاختبار (13) أكبر من القيمة الحرجة (5)، فإننا نفشل في رفض فرضية العدم.
5. تفسير النتائج.
وبما أننا فشلنا في رفض فرضية العدم، فليس لدينا أدلة كافية لنقول إن عدد نوبات الهلع التي يعاني منها المرضى في مجموعة الدواء الوهمي يختلف عن عدد نوبات الهلع التي يعاني منها المرضى في مجموعة الدواء الوهمي.
مثال 2
نريد أن نعرف ما إذا كانت الدراسة لمدة 30 دقيقة يوميًا لمدة أسبوع تساعد الطلاب على الأداء بشكل أفضل في الاختبار. يتم تعيين ما مجموعه 15 مريضا بشكل عشوائي للدراسة أو لا مجموعة الدراسة. وبعد أسبوع، يأخذ جميع الطلاب نفس الاختبار.
نتائج الاختبار لكلتا المجموعتين مبينة أدناه:
| يذاكر | لا دراسة |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
قم بإجراء اختبار Mann-Whitney U لمعرفة ما إذا كان هناك اختلاف في درجات الاختبار لمجموعة الدراسة مقارنة بالمجموعة التي لم تدرس. استخدم مستوى أهمية 0.01.
1. اذكر الافتراضات.
H 0 : المجموعتان متساويتان
ح أ : المجموعتان السكانيتان غير متساويتين
2. تحديد مستوى الأهمية لاستخدامه في الفرضية.
تخبرنا المشكلة أنه يجب علينا استخدام مستوى أهمية قدره 0.01.
3. ابحث عن إحصائية الاختبار.
تذكَّر أن إحصائية الاختبار يُشار إليها بـ U وهي الأصغر بين U 1 وU 2 ، كما هو محدد أدناه:
يو 1 = ن 1 ن 2 + ن 1 (ن 1 +1)/2 – ر 1
يو 2 = ن 1 ن 2 + ن 2 (ن 2 +1)/2 – ر 2
حيث n 1 وn 2 هما حجما العينة للعينتين 1 و2 على التوالي، وR 1 وR 2 هما مجموع رتب العينات 1 و2 على التوالي.
من أجل العثور على R 1 و R 2 ، نحتاج إلى دمج الملاحظات من كلا المجموعتين وترتيبها من الأصغر إلى الأكبر:
| يذاكر | لا دراسة |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
العينة الإجمالية: 72 ، 75 ، 80 ، 81، 84، 88 ، 89 ، 90 ، 91 ، 92 ، 93 ، 94 ، 95 ، 96 ، 99
الصفوف: 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9 ، 10 ، 11 ، 12 ، 13 ، 14 ، 15
R 1 = مجموع رتب العينة 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = مجموع الرتب للعينة 2 = 1+2+3+4+6+11+13 = 40
بعد ذلك، نستخدم أحجام العينات n 1 و n 2 بالإضافة إلى مجموع الرتب R 1 و R 2 للعثور على U 1 و U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
إحصائيات الاختبار لدينا هي الأصغر من U1 و U2 والتي تصادف أن تكون U=12.
ملاحظة: يمكننا أيضًا استخدام حاسبة اختبار Mann-Whitney U لتحديد أن U = 12.
4. ارفض أو لا ترفض الفرضية الصفرية.
باستخدام n 1 = 8 وn 2 = 7 بمستوى دلالة 0.01، يخبرنا جدول Mann-Whitney U أن القيمة الحرجة هي 6:
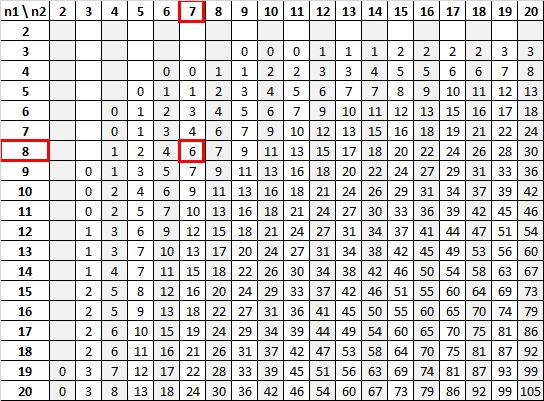
وبما أن إحصائية الاختبار (12) أكبر من القيمة الحرجة (6)، فإننا نفشل في رفض فرضية العدم.
5. تفسير النتائج.
وبما أننا فشلنا في رفض الفرضية الصفرية، فليس لدينا أدلة كافية لنقول إن درجات اختبار الطلاب الذين درسوا تختلف عن درجات الطلاب الذين لم يدرسوا.
مصادر إضافية
حاسبة اختبار مان ويتني يو
طاولة مان ويتني يو
كيفية إجراء اختبار مان ويتني يو في إكسل
كيفية إجراء اختبار مان ويتني يو في R
كيفية إجراء اختبار مان ويتني يو في بايثون
كيفية إجراء اختبار مان ويتني يو في SPSS
كيفية إجراء اختبار مان ويتني يو في ستاتا
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر