كيفية إجراء اختبار مربع الطاقة يدويًا (خطوة بخطوة)

يتم استخدام اختبار جودة الملاءمة لمربع كاي لتحديد ما إذا كان المتغير القاطع يتبع توزيعًا افتراضيًا أم لا.

يوضح المثال التالي خطوة بخطوة كيفية إجراء اختبار جودة الملاءمة لمربع كاي يدويًا.

اختبار جودة المطابقة بمربع كاي يدويًا

لنفترض أننا نعتقد أن نردًا معينًا هو الصحيح. بمعنى آخر، نحن نعتقد أن حجر النرد له نفس احتمالية الهبوط على الرقم 1، أو 2، أو 3، أو 4، أو 5، أو 6 في لفة معينة.

لاختبار ذلك، نرميها 60 مرة ونسجل العدد الذي تصل إليه في كل مرة. النتائج كما يلي:

• 1 :8 مرات
• 2 : 12 مرة
• 3 : 18 مرة
• 4 :9 مرات
• 5 :7 مرات
• 6 : 6 مرات

اتبع الخطوات التالية لإجراء اختبار جودة المطابقة لمربع كاي لتحديد ما إذا كان النرد عادلاً أم لا.

الخطوة الأولى: تحديد الفرضيات الصفرية والبديلة

• H ₀ (خالية): لأحجار النرد نفس احتمالية الهبوط على كل رقم.
• H ₁ (بديل): ليس لأحجار النرد نفس احتمالية الهبوط على كل رقم.

الخطوة الثانية: حساب التكرارات المرصودة والمتوقعة

بعد ذلك، لنقم بإنشاء جدول بالتكرارات الملحوظة والمتوقعة لكل رقم على حجر النرد:

ملاحظة : إذا اعتقدنا أن حجر النرد عادل، فهذا يعني أننا نتوقع أن يصل حجر النرد إلى كل رقم عددًا متساويًا من المرات – في هذه الحالة، 10 مرات لكل رقم.

الخطوة 3: حساب إحصائية الاختبار

يتم حساب إحصائية اختبار مربع كاي، X ² ، على النحو التالي:

• X ² = Σ(OE) ² / E

ويوضح الجدول التالي كيفية حساب إحصائية الاختبار هذه:

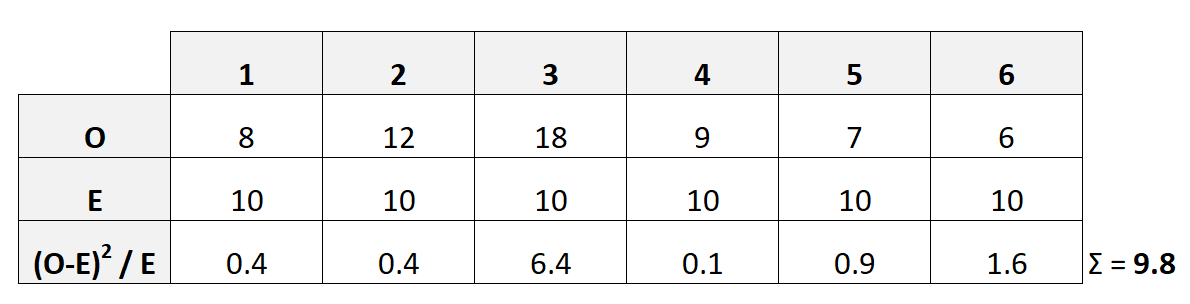
في هذه الحالة، X ² يتبين أن 9.8 .

الخطوة 4: ابحث عن القيمة الحرجة

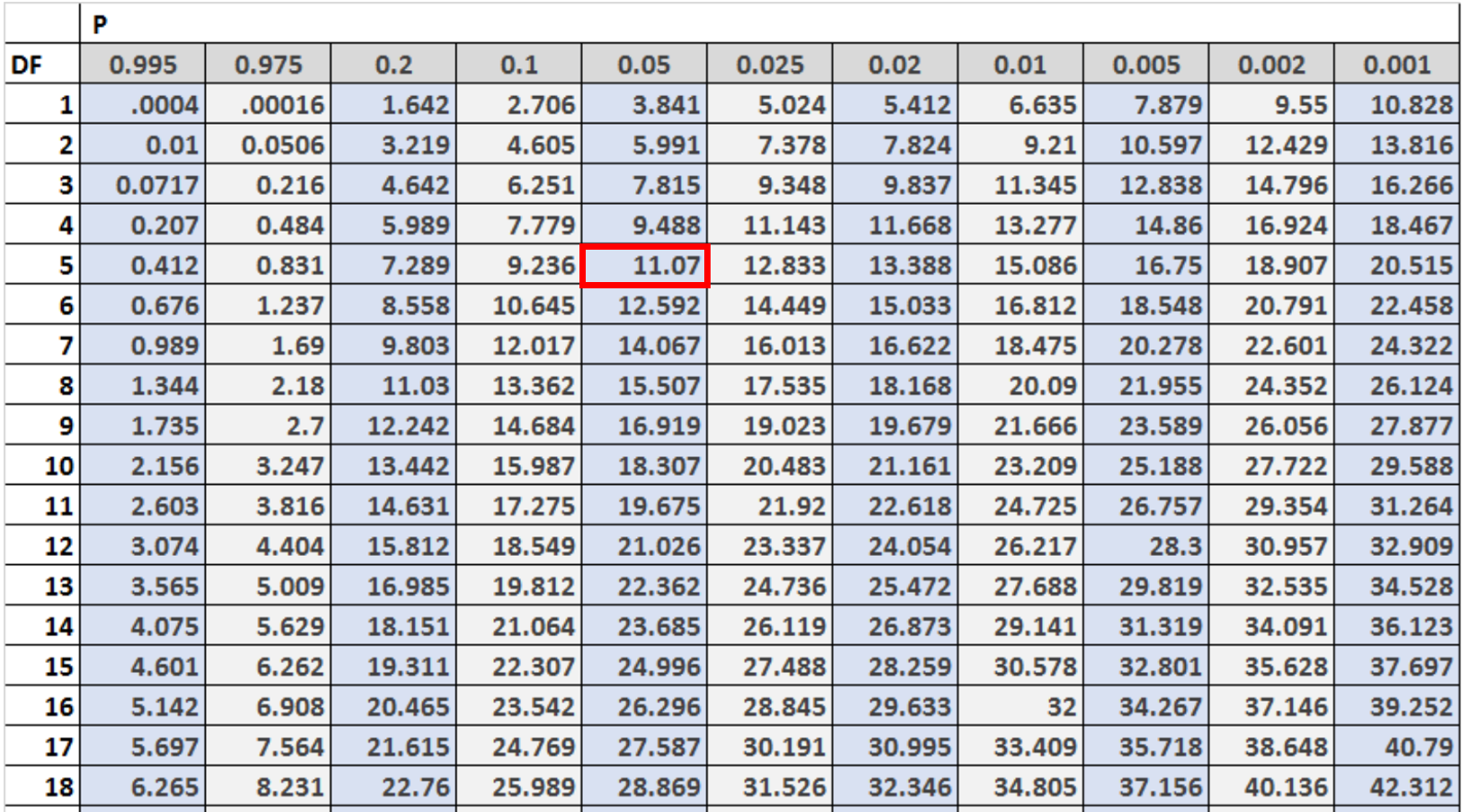
بعد ذلك، نحتاج إلى إيجاد القيمة الحرجة في جدول توزيع مربع كاي والتي تتوافق مع α = 0.05 وdf = (#categories – 1).

في هذه الحالة هناك 6 فئات، لذلك سوف نستخدم df = 6 – 1 = 5 .

يمكننا أن نرى أن القيمة الحرجة هي 11.07 .

الخطوة 5: رفض أو الفشل في رفض الفرضية الصفرية

وبما أن إحصائية الاختبار لدينا أقل من القيمة الحرجة، فإننا نفشل في رفض فرضية العدم. هذا يعني أنه ليس لدينا ما يكفي من الأدلة لنقول إن النرد غير عادل.

مصادر إضافية

توفر الموارد التالية معلومات إضافية حول اختبار جودة المطابقة لمربع كاي:

مقدمة لاختبار جودة المطابقة لمربع كاي
كيفية إجراء اختبار جودة الملاءمة لمربع كاي في R
حاسبة اختبار جودة المطابقة لمربع كاي