كيفية إجراء اختبار مدى جودة مربع كاي في برنامج spss

يتم استخدام اختبار جودة الملاءمة لمربع كاي لتحديد ما إذا كان المتغير القاطع يتبع توزيعًا افتراضيًا أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار جودة المطابقة لمربع كاي في برنامج SPSS.

مثال: اختبار جودة المطابقة لمربع كاي في برنامج SPSS

يقول صاحب متجر إن عددًا متساويًا من العملاء يأتون إلى متجره كل يوم من أيام الأسبوع. لاختبار هذه الفرضية، يقوم الباحث بتسجيل عدد العملاء الذين يأتون إلى المتجر في أسبوع معين ويجد ما يلي:

• الاثنين: 50 عميلاً
• الثلاثاء: 60 عميلاً
• الأربعاء: 40 عميلاً
• الخميس: 47 عميلاً
• الجمعة: 53 عميلاً

استخدم الخطوات التالية لإجراء اختبار مدى ملاءمة مربع كاي في SPSS لتحديد ما إذا كانت البيانات متوافقة مع مطالبة مالك المتجر.

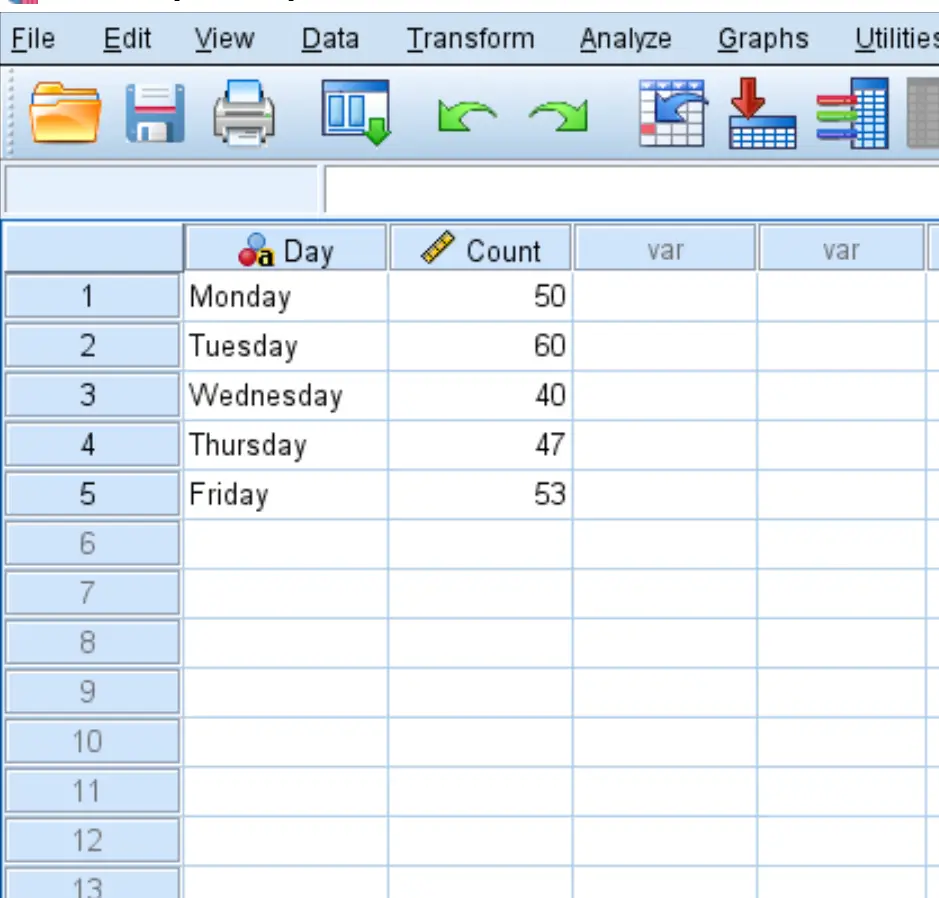
الخطوة 1: أدخل البيانات.

أولا قم بإدخال البيانات في برنامج SPSS بالتنسيق التالي:

الخطوة 2: استخدم الصناديق المرجحة.

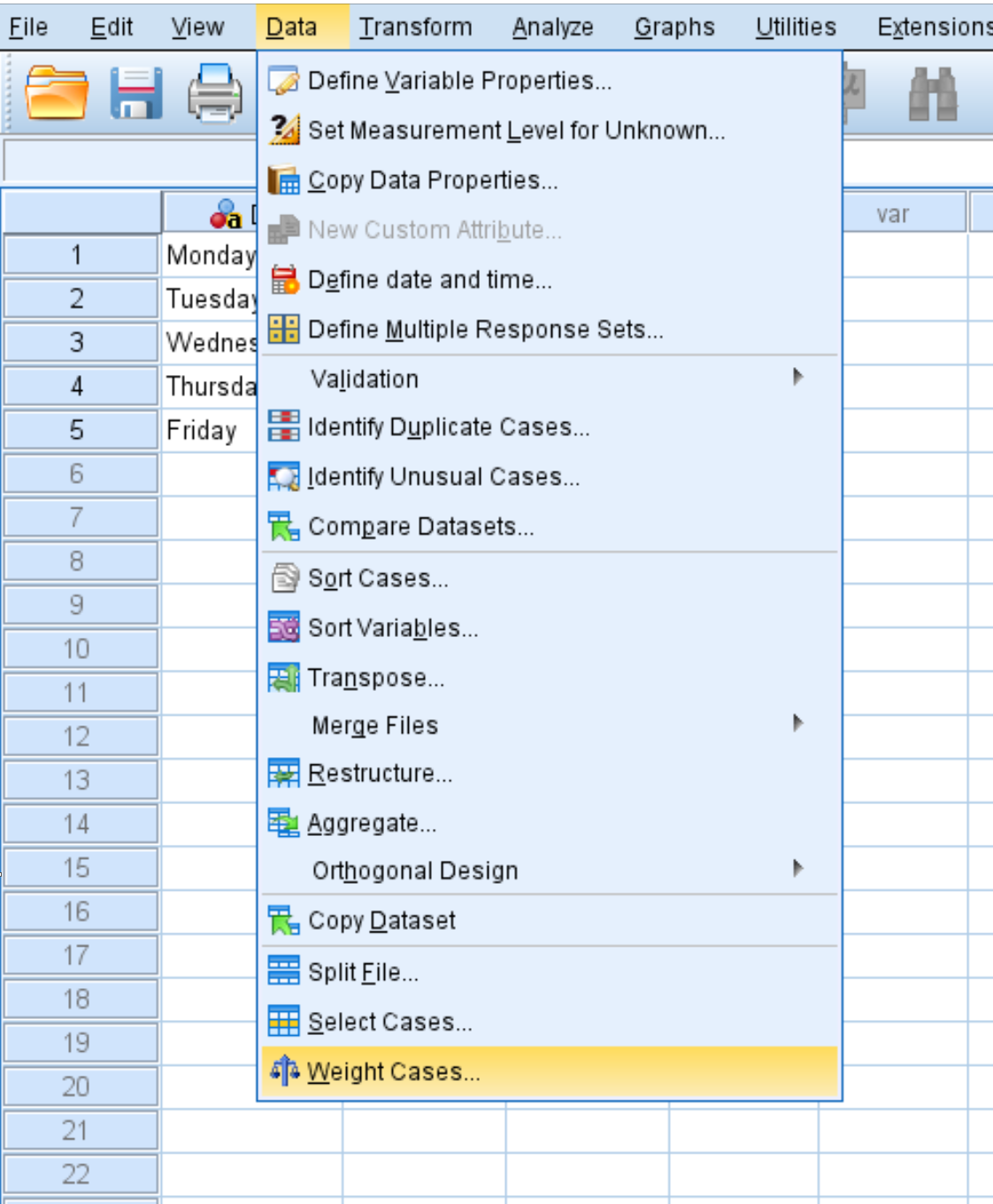
لكي يعمل الاختبار بشكل صحيح، نحتاج إلى إخبار SPSS أنه يجب ترجيح متغير “اليوم” بواسطة متغير “الرقم”.

انقر فوق علامة التبويب “البيانات” ، ثم انقر فوق “حالات الوزن” :

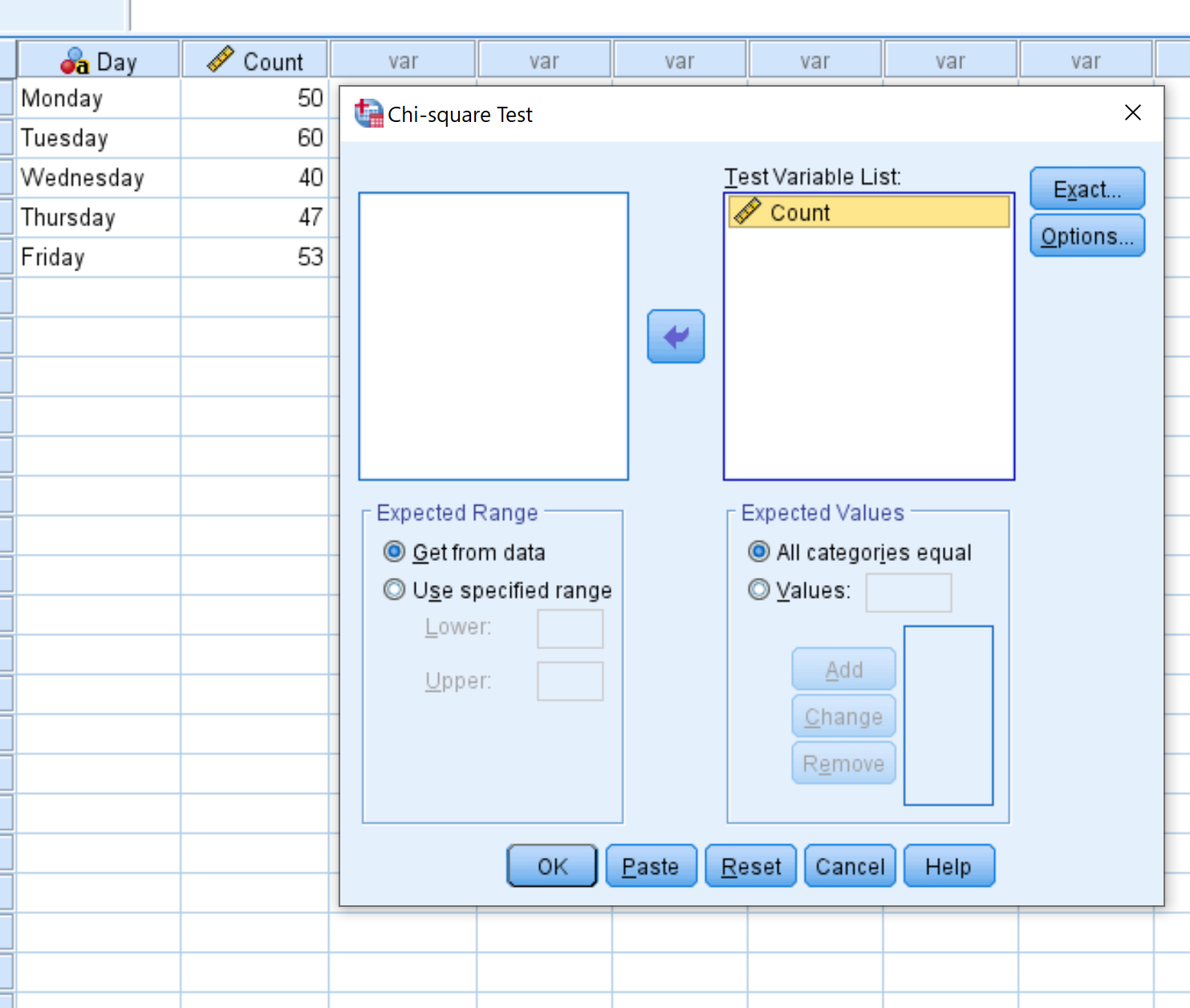
في النافذة الجديدة التي تظهر، اسحب متغير العدد إلى المنطقة المسماة قائمة متغيرات الاختبار. ثم انقر فوق موافق .

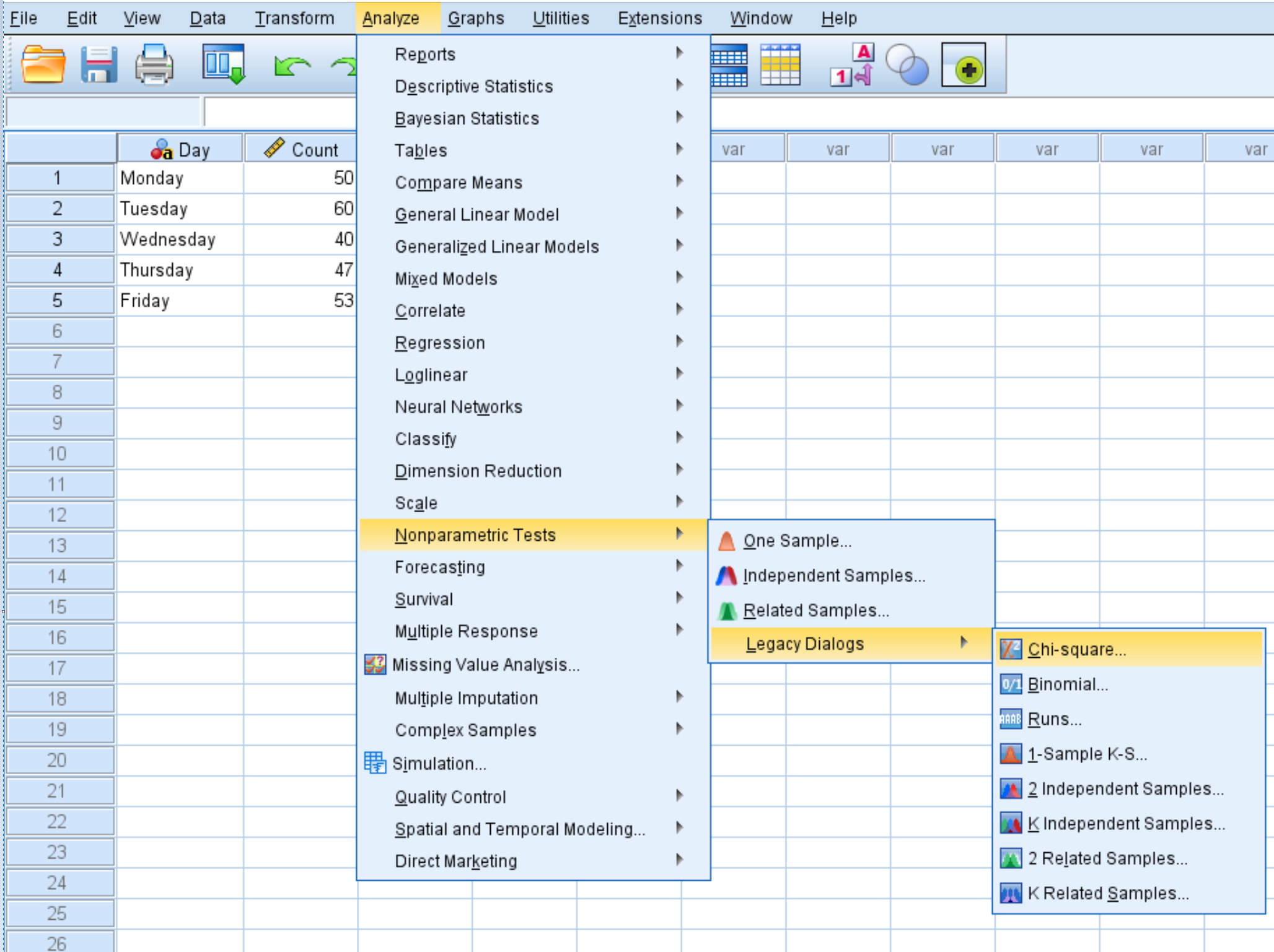
الخطوة 3: إجراء اختبار جودة المطابقة لمربع كاي.

انقر فوق علامة التبويب تحليل ، ثم الاختبارات اللامعلمية ، ثم مربعات الحوار القديمة ، ثم مربع الطاقة :

في النافذة الجديدة التي تظهر، اسحب متغير العدد إلى المنطقة المسماة قائمة متغيرات الاختبار.

اترك العلامة محددة بجوار جميع الفئات متساوية نظرًا لأن كل فئة من فئاتنا (أي أيام الأسبوع) لها نفس العدد المتوقع من الزوار كل يوم. ثم انقر فوق موافق .

الخطوة 4: تفسير النتائج .

بمجرد النقر فوق “موافق” ، ستظهر نتائج اختبار جودة المطابقة لمربع كاي:

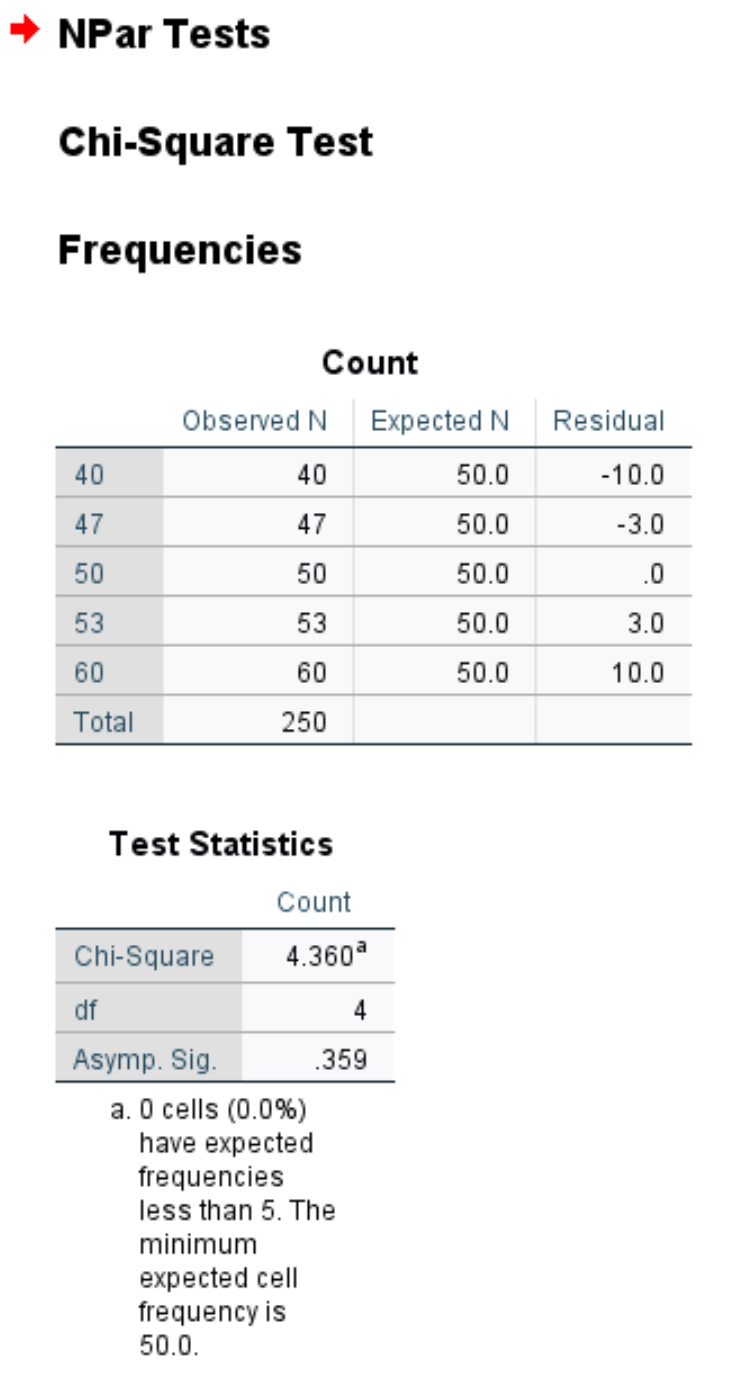
يوضح الجدول الأول عدد العملاء الملحوظ والمتوقع في كل يوم من أيام الأسبوع، بالإضافة إلى المتبقي (أي الفرق) بين الملاحظ والمتوقع.

يعرض الجدول الثاني الأرقام التالية:

مربع كاي: إحصائية اختبار مربع كاي وهي 4.36.

df: درجات الحرية، ويتم حسابها على النحو التالي: #categories-1 = 5-1 = 4.

أسيمب. Sig: القيمة p التي تقابل قيمة مربع كاي 4.36 مع 4 درجات حرية وهي 0.359. يمكن أيضًا العثور على هذه القيمة باستخدام نتيجة مربع كاي إلى حاسبة القيمة P.

وبما أن القيمة p (0.359) لا تقل عن 0.05، فإننا نفشل في رفض فرضية العدم. وهذا يعني أنه ليس لدينا ما يكفي من الأدلة لنقول أن التوزيع الحقيقي للعملاء يختلف عن ذلك الذي أبلغ عنه صاحب المتجر.