كيفية حساب الارتباط الذاتي في r
يقيس الارتباط التلقائي درجة التشابه بين السلسلة الزمنية والنسخة المتأخرة من نفسها على فترات زمنية متتالية.
ويطلق عليه أيضًا أحيانًا “الارتباط التسلسلي” أو “الارتباط المتأخر” لأنه يقيس العلاقة بين القيم الحالية للمتغير وقيمه التاريخية.
عندما يكون الارتباط الذاتي في سلسلة زمنية مرتفعًا، يصبح من السهل التنبؤ بالقيم المستقبلية بمجرد الإشارة إلى القيم السابقة.
كيفية حساب الارتباط الذاتي في R
لنفترض أن لدينا السلسلة الزمنية التالية في R التي توضح قيمة متغير معين لمدة 15 فترة مختلفة:
#define data
x <- c(22, 24, 25, 25, 28, 29, 34, 37, 40, 44, 51, 48, 47, 50, 51)
يمكننا حساب الارتباط التلقائي لكل تأخير في السلسلة الزمنية باستخدام الدالة acf() من مكتبة tseries :
library (tseries) #calculate autocorrelations acf(x, pl= FALSE ) 0 1 2 3 4 5 6 7 8 9 10 1.000 0.832 0.656 0.491 0.279 0.031 -0.165 -0.304 -0.401 -0.458 -0.450 11 -0.369
وطريقة تفسير النتيجة هي كما يلي:
- الارتباط الذاتي عند التأخر 0 هو 1 .
- الارتباط التلقائي في التأخر 1 هو 0.832 .
- الارتباط التلقائي في التأخر 2 هو 0.656 .
- الارتباط التلقائي في التأخر 3 هو 0.491 .
وما إلى ذلك وهلم جرا.
يمكننا أيضًا تحديد عدد الفترات الزمنية التي سيتم عرضها باستخدام الوسيطة lag :
#calculate autocorrelations up to lag=5 acf(x, lag=5, pl= FALSE ) Autocorrelations of series 'x', by lag 0 1 2 3 4 5 1.000 0.832 0.656 0.491 0.279 0.031
كيفية رسم وظيفة الارتباط الذاتي في R
يمكننا رسم دالة الارتباط التلقائي لسلسلة زمنية في R ببساطة عن طريق عدم استخدام الوسيطة pl=FALSE :
#plot autocorrelation function
acf(x)
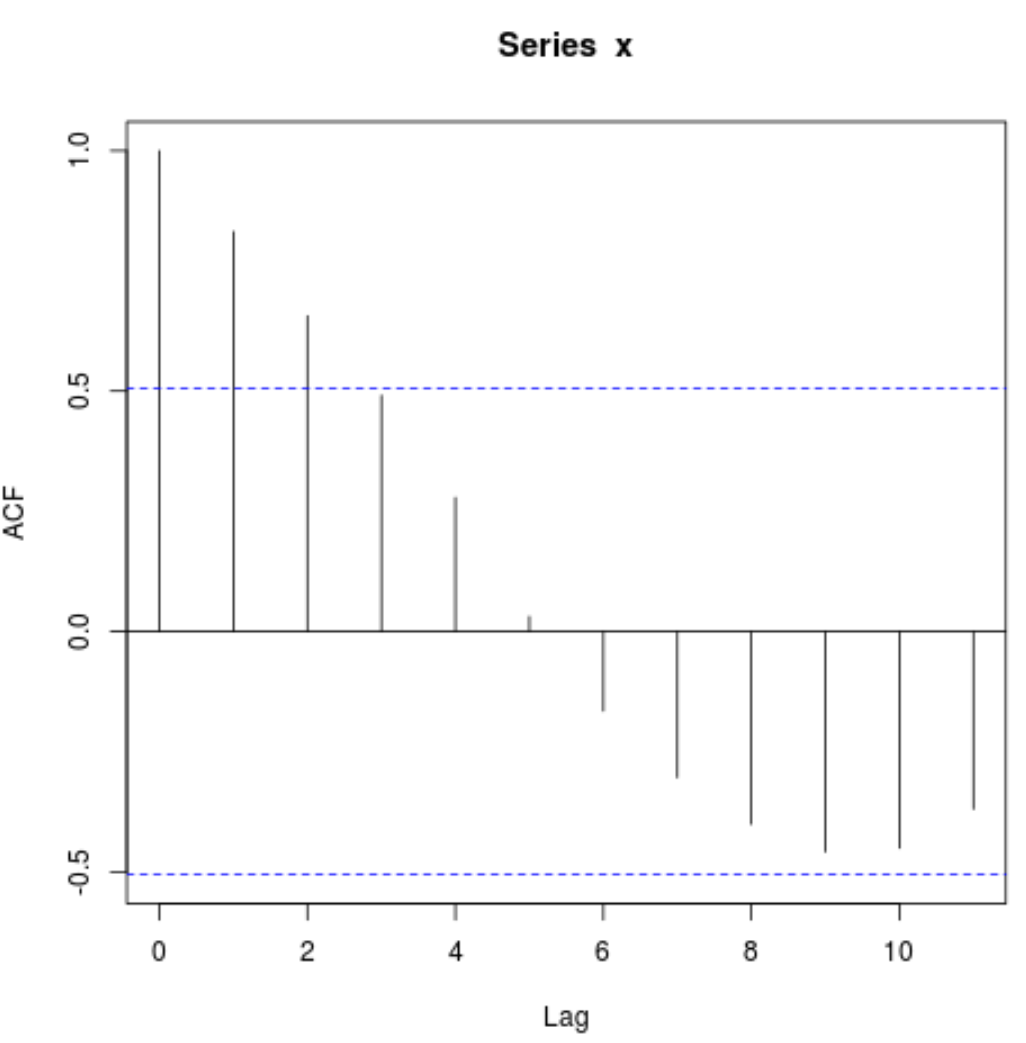
يعرض المحور السيني عدد الفترات الزمنية ويعرض المحور الصادي الارتباط التلقائي عند هذا العدد من الفترات الزمنية. افتراضيًا، يبدأ المخطط عند lag = 0 وسيكون الارتباط التلقائي دائمًا 1 عند lag = 0.
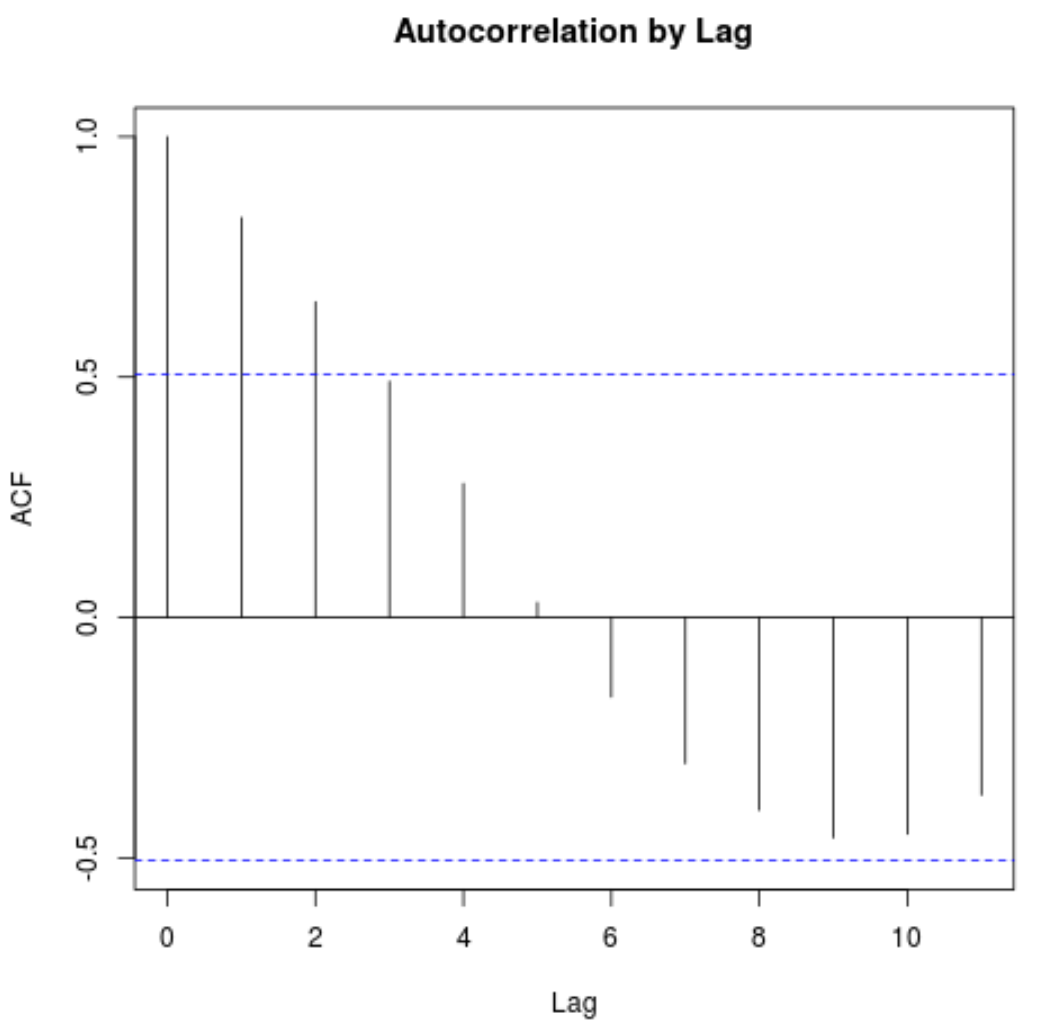
يمكنك أيضًا تحديد عنوان مختلف للحبكة باستخدام الوسيطة الرئيسية :
#plot autocorrelation function with custom title acf(x, main=' Autocorrelation by Lag ')
مصادر إضافية
كيفية حساب الارتباط التلقائي في بايثون
كيفية حساب الارتباط التلقائي في إكسل