الارتباط مقابل الانحدار: ما هو الفرق؟

الارتباط والانحدار هما مصطلحان إحصائيان مرتبطان، ولكن ليسا متطابقين تمامًا.

في هذا البرنامج التعليمي، سنقدم شرحًا موجزًا لكلا المصطلحين ونشرح مدى تشابههما واختلافهما.

ما هو الارتباط؟

يقيس الارتباط الارتباط الخطي بين متغيرين، x و y . لها قيمة بين -1 و 1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية التي تحتوي على متغيرين: (1) ساعات الدراسة و(2) درجات الاختبار التي تم تلقيها لـ 20 طالبًا مختلفًا:

إذا أنشأنا مخططًا متناثرًا لساعات الدراسة مقابل نتائج الامتحانات، فهذا هو الشكل الذي سيبدو عليه:

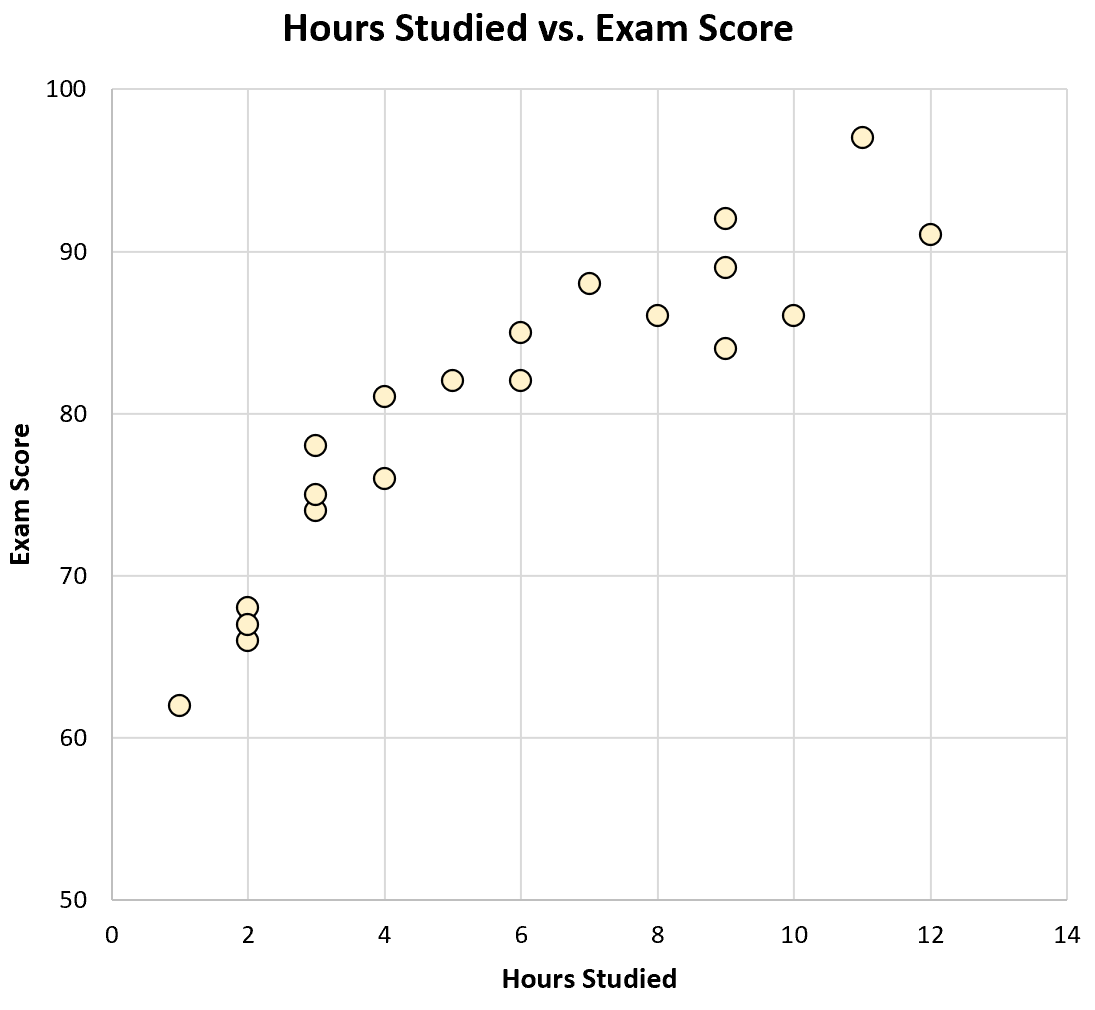
بمجرد النظر إلى الرسم البياني، يمكننا أن نرى أن الطلاب الذين يدرسون أكثر يميلون إلى الأداء بشكل أفضل في الامتحانات. وبعبارة أخرى، يمكننا أن نرى بصريا أن هناك علاقة إيجابية بين المتغيرين.

باستخدام الآلة الحاسبة، يمكننا أن نرى أن الارتباط بين هذين المتغيرين هو r = 0.915 . وبما أن هذه القيمة قريبة من 1، فهذا يؤكد أن هناك علاقة إيجابية قوية بين المتغيرين.

ما هو الانحدار؟

الانحدار هو أسلوب يمكننا استخدامه لفهم كيفية تأثير تغيير قيم المتغير x على قيم المتغير y .

يستخدم نموذج الانحدار متغيرًا واحدًا، x ، كمتغير متوقع والمتغير الآخر، y ، كمتغير الاستجابة . ثم يجد معادلة بالشكل التالي الذي يصف العلاقة بين المتغيرين بشكل أفضل:

ŷ = ب ₀ + ب ₁ س

ذهب:

• ŷ: القيمة المتوقعة لمتغير الاستجابة
• b ₀ : الإحداثي عند نقطة الأصل (قيمة y عندما تكون x مساوية للصفر)
• ب ₁ : معامل الانحدار (متوسط الزيادة في y لكل وحدة زيادة في x)
• x: قيمة المتغير التنبؤي

على سبيل المثال، خذ بعين الاعتبار مجموعة البيانات السابقة لدينا:

وباستخدام حاسبة الانحدار الخطي نجد أن المعادلة التالية تصف العلاقة بين هذين المتغيرين بشكل أفضل:

درجة الامتحان المتوقعة = 65.47 + 2.58*(ساعات الدراسة)

طريقة تفسير هذه المعادلة هي:

• درجة الامتحان المتوقعة للطالب الذي يدرس صفر ساعة هي 65.47 .
• متوسط الزيادة في درجة الامتحان المرتبطة بساعة إضافية من الدراسة هو 2.58 .

يمكننا أيضًا استخدام هذه المعادلة للتنبؤ بالنتيجة التي سيحصل عليها الطالب بناءً على عدد الساعات التي يدرسها.

على سبيل المثال الطالب الذي يدرس 6 ساعات يجب أن يحصل على درجة 80.95 :

درجة الامتحان المتوقعة = 65.47 + 2.58*(6) = 80.95 .

يمكننا أيضًا رسم هذه المعادلة كخط على مخطط مبعثر:

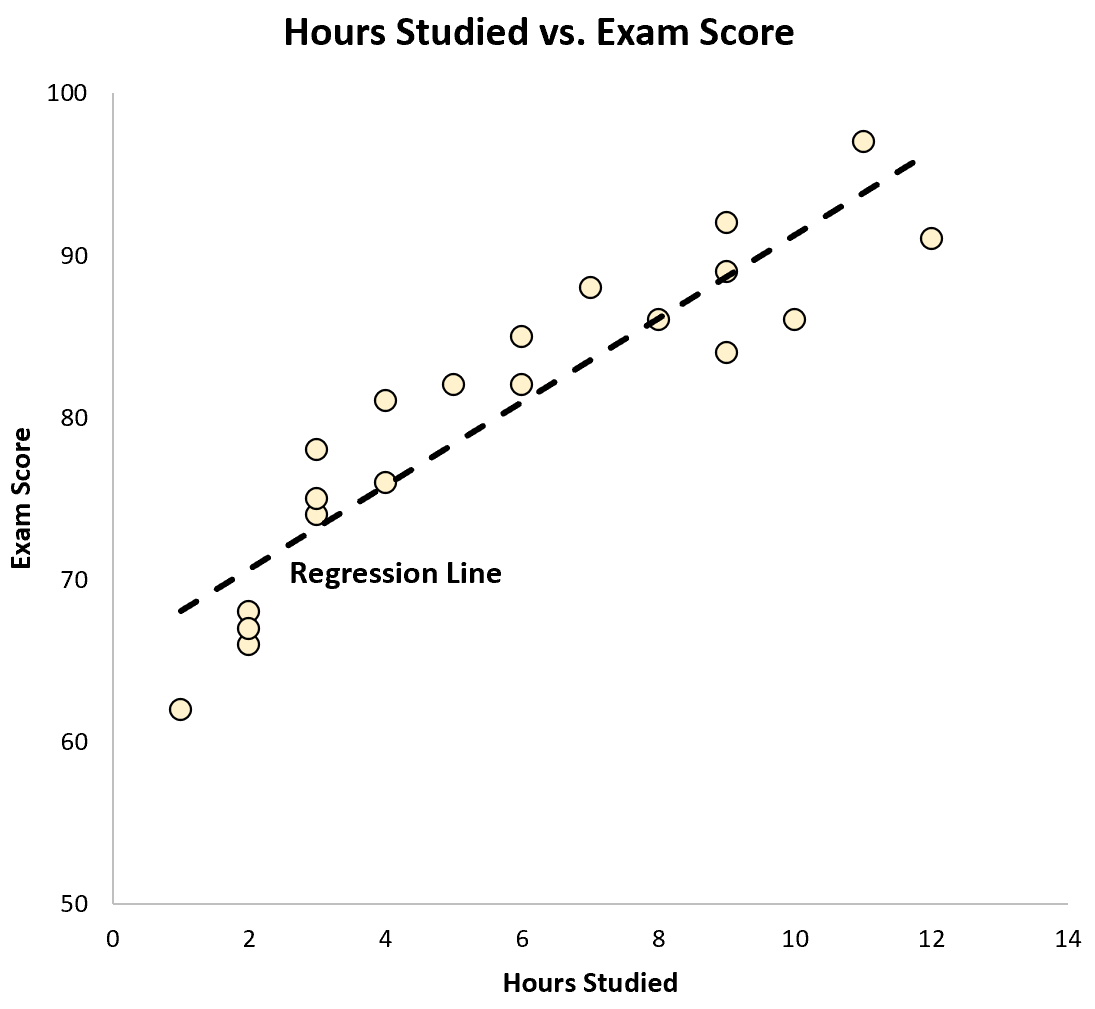
يمكننا أن نرى أن خط الانحدار “يناسب” البيانات بشكل جيد.

أذكر سابقًا أن الارتباط بين هذين المتغيرين كان r = 0.915 . وتبين أنه يمكننا تربيع هذه القيمة والحصول على رقم يسمى “r تربيع” الذي يصف إجمالي نسبة التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة المتغير المتنبئ.

في هذا المثال, r ² = 0.915 ² = 0.837 . وهذا يعني أن 83.7% من التباين في درجات الامتحان يمكن تفسيره بعدد الساعات المدروسة.

الارتباط مقابل الانحدار: أوجه التشابه والاختلاف

فيما يلي ملخص لأوجه التشابه والاختلاف بين الارتباط والانحدار:

التشابه:

• كلاهما يحدد اتجاه العلاقة بين متغيرين.
• كلاهما يحدد قوة العلاقة بين متغيرين.

اختلافات:

• الانحدار قادر على إظهار علاقة السبب والنتيجة بين متغيرين. الارتباط لا يفعل ذلك.
• الانحدار قادر على استخدام معادلة للتنبؤ بقيمة متغير واحد، استنادا إلى قيمة متغير آخر. الارتباط لا يفعل ذلك.
• يستخدم الانحدار معادلة لتحديد العلاقة بين متغيرين. يستخدم الارتباط رقمًا واحدًا.

مصادر إضافية

تقدم البرامج التعليمية التالية مزيدًا من التوضيحات المتعمقة للموضوعات التي تتناولها هذه المقالة.

مقدمة لمعامل ارتباط بيرسون
مقدمة للانحدار الخطي البسيط
حاسبة الانحدار الخطي البسيط
ما هي قيمة R-squared الجيدة؟