الانحدار الأسي في بايثون (خطوة بخطوة)
الانحدار الأسي هو نوع من الانحدار يمكن استخدامه لنمذجة المواقف التالية:
1. النمو الأسي: يبدأ النمو ببطء ثم يتسارع بسرعة وبلا حدود.
2. الاضمحلال الأسي: يبدأ الاضمحلال بسرعة ثم يتباطأ ليقترب أكثر فأكثر من الصفر.

تأخذ معادلة نموذج الانحدار الأسي الشكل التالي:
ص = أب س
ذهب:
- y: متغير الاستجابة
- x: المتغير التنبؤي
- a,b: معاملات الانحدار التي تصف العلاقة بين x و y
يوضح المثال التالي خطوة بخطوة كيفية إجراء الانحدار الأسي في بايثون.
الخطوة 1: إنشاء البيانات
أولاً، لنقم بإنشاء بيانات وهمية لمتغيرين: x و y :
import numpy as np x = np. arange (1, 21, 1) y = np. array ([1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113])
الخطوة 2: تصور البيانات
بعد ذلك، لنقم بإنشاء مخطط تشتت سريع لتصور العلاقة بين x و y :
import matplotlib. pyplot as plt plt. scatter (x,y) plt. show ()
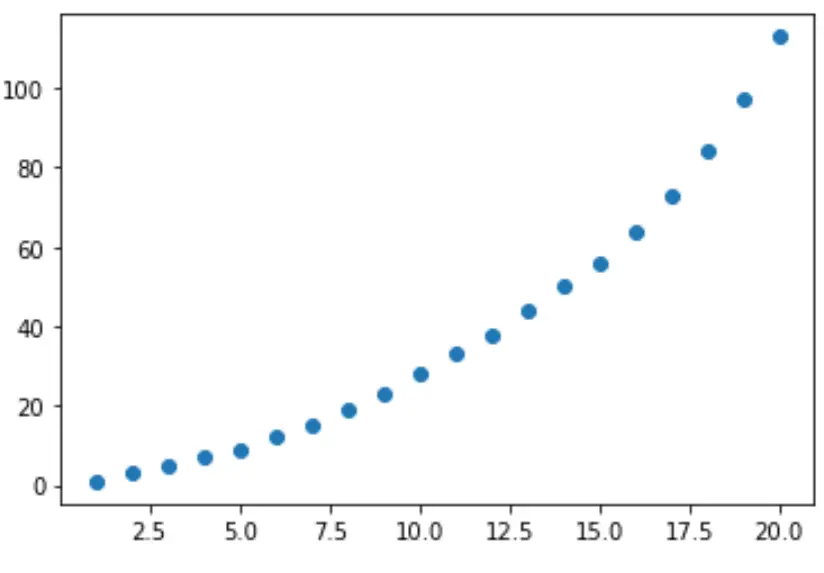
من الرسم البياني، يمكننا أن نرى أن هناك نمط نمو أسي واضح بين المتغيرين.
وبالتالي، يبدو من الحكمة ملاءمة معادلة الانحدار الأسي لوصف العلاقة بين المتغيرات، بدلاً من نموذج الانحدار الخطي.
الخطوة 3: تناسب نموذج الانحدار الأسي
بعد ذلك، سوف نستخدم الدالة polyfit() لتناسب نموذج الانحدار الأسي، باستخدام اللوغاريتم الطبيعي لـ y كمتغير الاستجابة و x كمتغير متوقع:
#fit the model fit = np. polyfit (x, np. log (y), 1) #view the output of the model print(fit) [0.2041002 0.98165772]
وبناء على النتيجة يمكن كتابة معادلة الانحدار الأسي المجهزة على النحو التالي:
قانون الجنسية (ذ) = 0.9817 + 0.2041 (س)
وبتطبيق e على كلا الطرفين، يمكننا إعادة كتابة المعادلة على النحو التالي:
ص = 2.6689 * 1.2264x
يمكننا استخدام هذه المعادلة للتنبؤ بمتغير الاستجابة y بناءً على قيمة المتغير المتنبئ x . على سبيل المثال، إذا كانت x = 12، فسنتوقع أن y ستكون 30.897 :
ص = 2.6689 * 1.2264 12 = 30.897
المكافأة: لا تتردد في استخدام حاسبة الانحدار الأسي عبر الإنترنت لحساب معادلة الانحدار الأسي تلقائيًا لمتنبئ معين ومتغير استجابة.
مصادر إضافية
كيفية إجراء الانحدار الخطي البسيط في بايثون
كيفية إجراء الانحدار متعدد الحدود في بايثون
كيفية إجراء الانحدار الكمي في بايثون