كيفية إجراء الانحدار التربيعي في بايثون

الانحدار التربيعي هو نوع من الانحدار يمكننا استخدامه لتحديد العلاقة بين متغير متنبئ ومتغير استجابة عندما تكون العلاقات الحقيقية تربيعية، والتي قد تبدو مثل “U” أو “U” مقلوب على الرسم البياني.

أي أنه مع زيادة المتغير المتنبئ، يميل متغير الاستجابة إلى الزيادة أيضًا، ولكن بعد نقطة معينة يبدأ متغير الاستجابة في الانخفاض مع استمرار المتغير المتنبئ في الزيادة.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار التربيعي في بايثون.

مثال: الانحدار التربيعي في بايثون

لنفترض أن لدينا بيانات عن عدد ساعات العمل أسبوعيًا ومستوى السعادة المُبلغ عنه (على مقياس من 0 إلى 100) لـ 16 شخصًا مختلفًا:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

إذا قمنا بعمل مخطط مبعثر بسيط لهذه البيانات، يمكننا أن نرى أن العلاقة بين المتغيرين على شكل حرف “U”:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

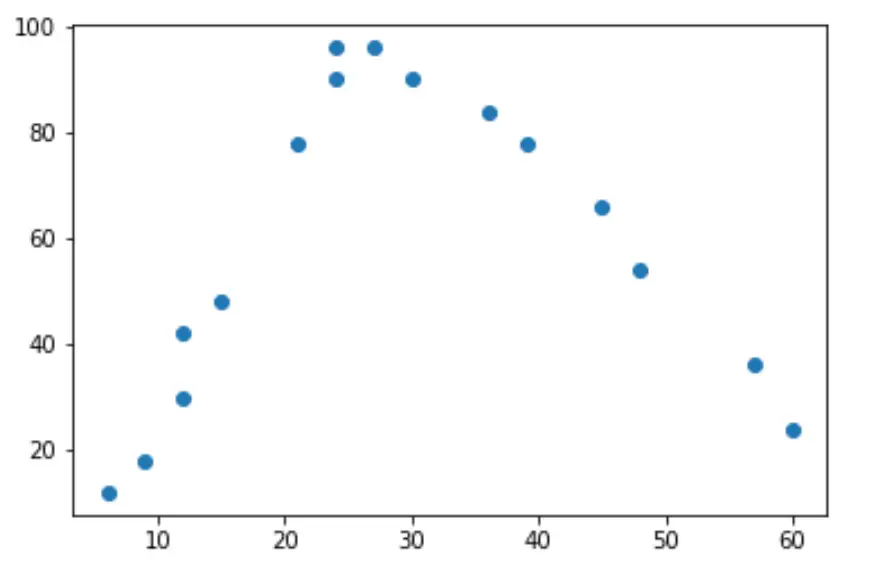
ومع زيادة ساعات العمل، تزداد السعادة أيضًا، ولكن بمجرد أن تتجاوز ساعات العمل حوالي 35 ساعة أسبوعيًا، تبدأ السعادة في الانخفاض.

وبسبب هذا الشكل “U”، فهذا يعني أن الانحدار التربيعي من المحتمل أن يكون مرشحًا جيدًا لقياس العلاقة بين المتغيرين.

لإجراء انحدار تربيعي فعليًا، يمكننا ملاءمة نموذج انحدار متعدد الحدود بدرجة 2 باستخدام الدالة numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

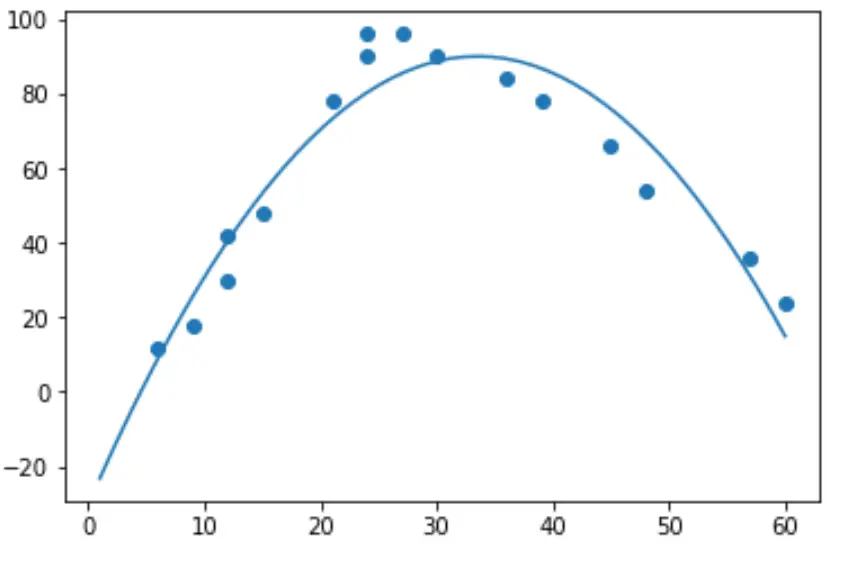
يمكننا الحصول على معادلة الانحدار متعدد الحدود المجهزة عن طريق طباعة معاملات النموذج:

 print (model)

-0.107x 2 + 7.173x - 30.25

معادلة الانحدار التربيعية المجهزة هي:

السعادة = -0.107(ساعات) ² + 7.173(ساعات) – 30.25

يمكننا استخدام هذه المعادلة لحساب مستوى السعادة المتوقع للفرد بناءً على ساعات عمله. على سبيل المثال، مستوى السعادة المتوقع للشخص الذي يعمل 30 ساعة أسبوعياً هو:

السعادة = -0.107(30) ² + 7.173(30) – 30.25 = 88.64 .

يمكننا أيضًا كتابة دالة قصيرة للحصول على مربع R للنموذج، وهي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغيرات المتوقعة.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

في هذا المثال، مربع R للنموذج هو 0.9092 .

وهذا يعني أن 90.92% من التباين في مستويات السعادة المبلغ عنها يمكن تفسيره من خلال المتغيرات المتنبئة.

مصادر إضافية

كيفية إجراء الانحدار متعدد الحدود في بايثون
كيفية إجراء الانحدار التربيعي في R
كيفية إجراء الانحدار التربيعي في إكسيل