كيفية إجراء الانحدار التربيعي في r

عندما يكون بين متغيرين علاقة خطية، يمكننا غالبًا استخدام الانحدار الخطي البسيط لتحديد العلاقة بينهما.

ومع ذلك، عندما يكون لمتغيرين علاقة تربيعية، يمكننا استخدام الانحدار التربيعي لتحديد العلاقة بينهما.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار التربيعي في R.

مثال: الانحدار التربيعي في R

لنفترض أننا نريد أن نفهم العلاقة بين عدد ساعات العمل والسعادة المبلغ عنها. لدينا البيانات التالية عن عدد ساعات العمل أسبوعيًا ومستوى السعادة المُبلغ عنه (على مقياس من 0 إلى 100) لـ 11 شخصًا مختلفًا:

استخدم الخطوات التالية لتناسب نموذج الانحدار التربيعي في R.

الخطوة 1: أدخل البيانات.

أولاً، سنقوم بإنشاء إطار بيانات يحتوي على بياناتنا:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

الخطوة 2: تصور البيانات.

بعد ذلك، سوف نقوم بإنشاء مخطط تشتت بسيط لتصور البيانات.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

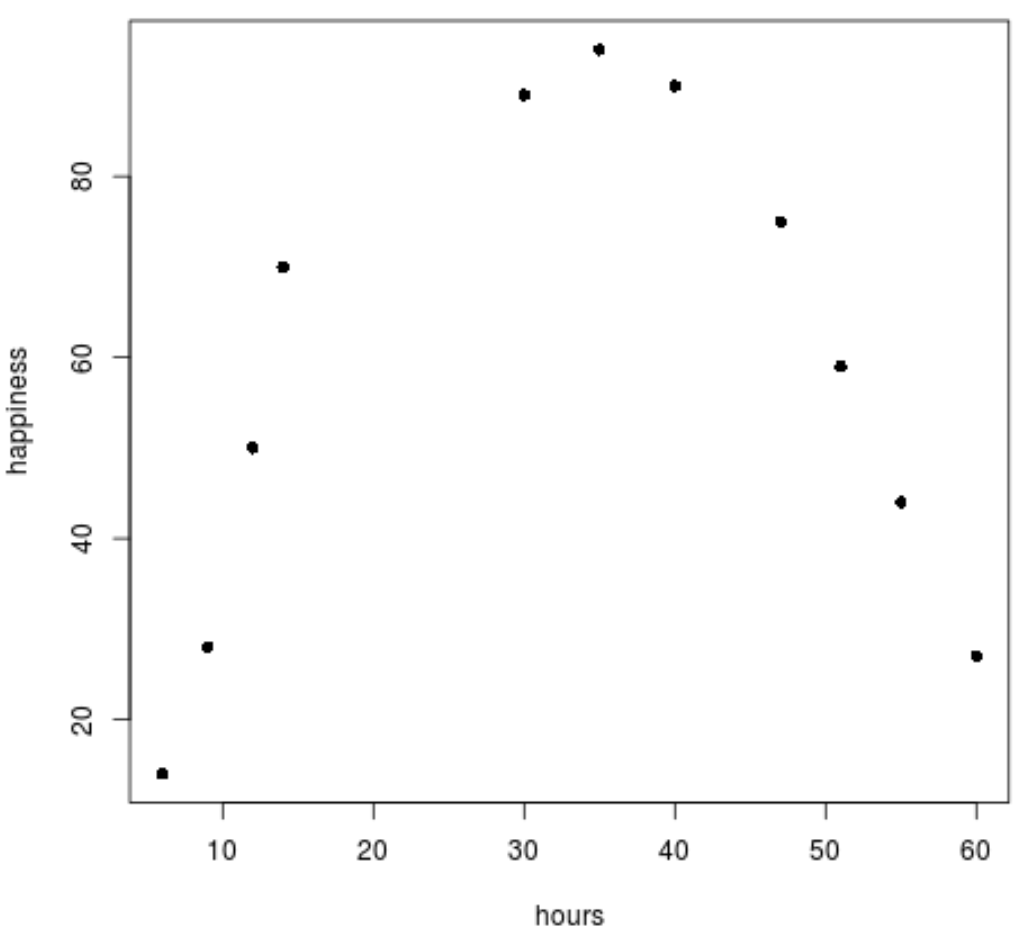
يمكننا أن نرى بوضوح أن البيانات لا تتبع نمطًا خطيًا.

الخطوة 3: تناسب نموذج الانحدار الخطي البسيط.

بعد ذلك، سنقوم بتركيب نموذج انحدار خطي بسيط لمعرفة مدى ملاءمته للبيانات:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

إجمالي التباين في السعادة الذي أوضحه النموذج هو 4.46% فقط، كما هو موضح من خلال قيمة R-squared المتعددة.

الخطوة 4: تناسب نموذج الانحدار التربيعي.

بعد ذلك، سوف نقوم بتركيب نموذج الانحدار التربيعي.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

وارتفع التباين الكلي في السعادة المفسر بالنموذج إلى 96.02% .

يمكننا استخدام الكود التالي لتصور مدى ملاءمة النموذج للبيانات:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

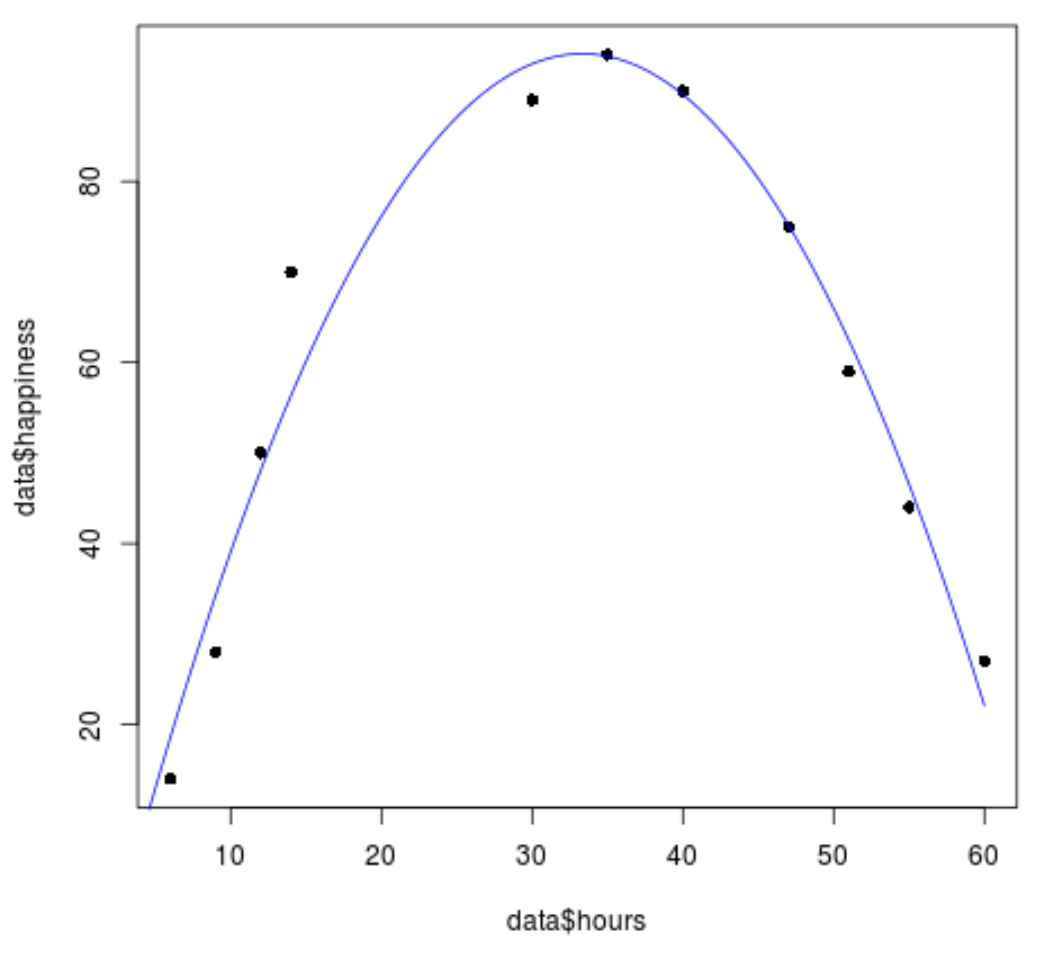
يمكننا أن نرى أن خط الانحدار التربيعي يناسب قيم البيانات بشكل جيد.

الخطوة 5: تفسير نموذج الانحدار التربيعي.

رأينا في الخطوة السابقة أن نتيجة نموذج الانحدار التربيعي كانت:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

بناءً على المعاملات المعروضة هنا، سيكون الانحدار التربيعي المعدل كما يلي:

السعادة = -0.1012 (ساعة) ² + 6.7444 (ساعة) – 18.2536

يمكننا استخدام هذه المعادلة للعثور على السعادة المتوقعة للفرد، بالنظر إلى عدد الساعات التي يعملها في الأسبوع.

على سبيل المثال، الشخص الذي يعمل 60 ساعة في الأسبوع سيكون لديه مستوى سعادة يبلغ 22.09 :

السعادة = -0.1012(60) ² + 6.7444(60) – 18.2536 = 22.09

وعلى العكس من ذلك، فإن الشخص الذي يعمل 30 ساعة أسبوعيًا يجب أن يكون مستوى سعادته 92.99 :

السعادة = -0.1012(30) ² + 6.7444(30) – 18.2536 = 92.99