كيفية إجراء الانحدار الخطي البسيط في sas

الانحدار الخطي البسيط هو أسلوب يمكننا استخدامه لفهم العلاقة بين متغير متنبئ ومتغير استجابة .

تعثر هذه التقنية على السطر الذي “يناسب” البيانات بشكل أفضل ويأخذ النموذج التالي:

ŷ = ب ₀ + ب ₁ س

ذهب:

• ŷ : قيمة الاستجابة المقدرة
• ب ₀ : أصل خط الانحدار
• ب ₁ : ميل خط الانحدار

تساعدنا هذه المعادلة على فهم العلاقة بين المتغير المتنبئ ومتغير الاستجابة.

يوضح المثال التالي خطوة بخطوة كيفية إجراء انحدار خطي بسيط في SAS.

الخطوة 1: إنشاء البيانات

في هذا المثال، سنقوم بإنشاء مجموعة بيانات تحتوي على إجمالي عدد ساعات الدراسة ودرجة الاختبار النهائي لـ 15 طالبًا.

سوف نقوم بتركيب نموذج انحدار خطي بسيط باستخدام الساعات كمتغير متوقع والنتيجة كمتغير الاستجابة.

يوضح الكود التالي كيفية إنشاء مجموعة البيانات هذه في SAS:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

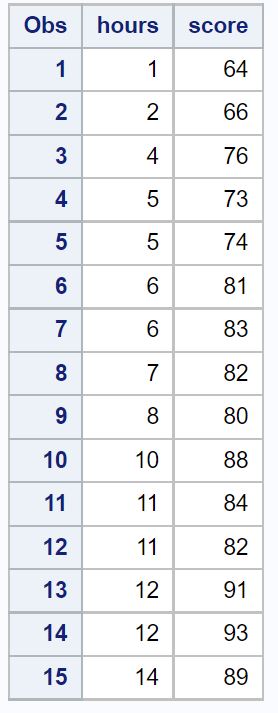
الخطوة 2: تناسب نموذج الانحدار الخطي البسيط

بعد ذلك، سوف نستخدم proc reg ليناسب نموذج الانحدار الخطي البسيط:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

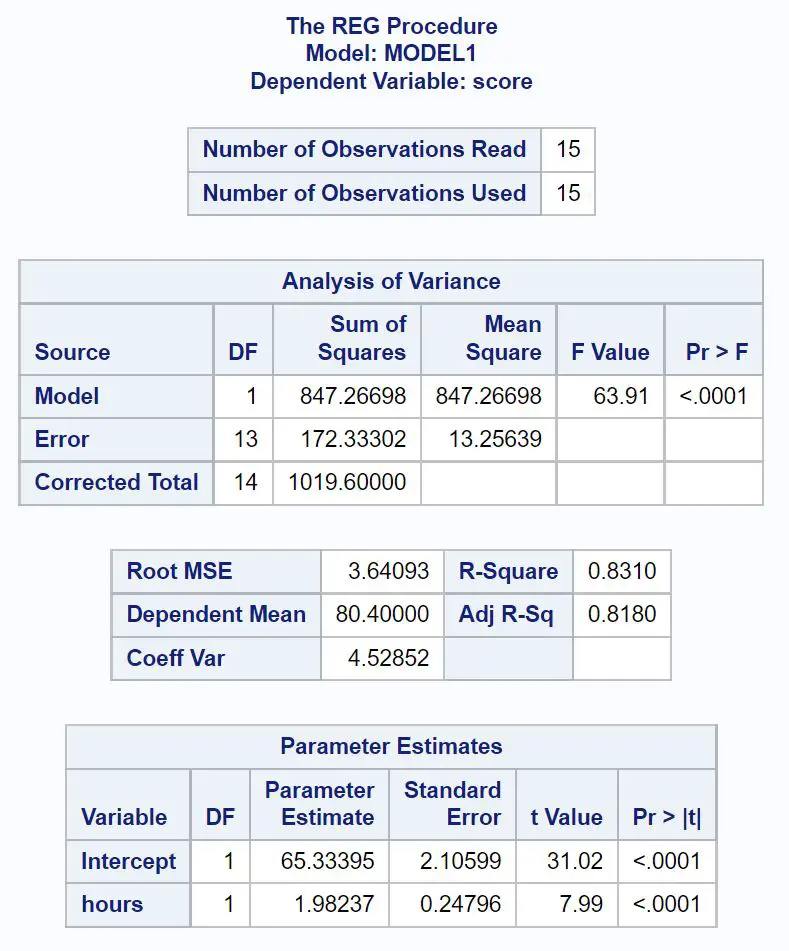
وإليك كيفية تفسير أهم القيم من كل جدول في النتيجة:

جدول تحليل الفجوة:

القيمة F الإجمالية لنموذج الانحدار هي 63.91 والقيمة p المقابلة هي <0.0001 .

وبما أن هذه القيمة p أقل من 0.05، فإننا نستنتج أن نموذج الانحدار ككل له دلالة إحصائية. بمعنى آخر، تعتبر الساعات متغيرًا مفيدًا للتنبؤ بنتائج الامتحانات.

الجدول المناسب للنموذج:

تخبرنا قيمة R-Square بنسبة التباين في درجات الامتحان التي يمكن تفسيرها بعدد ساعات الدراسة.

بشكل عام، كلما زادت قيمة R-squared لنموذج الانحدار، كلما كانت متغيرات التوقع أفضل في التنبؤ بقيمة متغير الاستجابة.

وفي هذه الحالة يمكن تفسير 83.1% من التباين في درجات الامتحان بعدد الساعات المدروسة. وهذه القيمة عالية جدًا، مما يشير إلى أن ساعات الدراسة تعد متغيرًا مفيدًا جدًا في التنبؤ بنتائج الامتحانات.

جدول تقديرات المعلمة:

من هذا الجدول يمكننا أن نرى معادلة الانحدار المجهزة:

النتيجة = 65.33 + 1.98*(ساعات)

نفسر هذا على أنه يعني أن كل ساعة إضافية تتم دراستها ترتبط بمتوسط زيادة قدره 1.98 نقطة في درجة الامتحان.

تخبرنا القيمة الأصلية أن متوسط درجات الامتحان للطالب الذي يدرس لمدة صفر ساعة هو 65.33 .

يمكننا أيضًا استخدام هذه المعادلة للعثور على درجة الامتحان المتوقعة بناءً على عدد الساعات التي يدرسها الطالب.

على سبيل المثال، الطالب الذي يدرس لمدة 10 ساعات يجب أن يحقق درجة الامتحان 85.13 :

النتيجة = 65.33 + 1.98*(10) = 85.13

وبما أن القيمة p (<0.0001) للساعات أقل من 0.05 في هذا الجدول، فإننا نستنتج أن هذا متغير ذو دلالة إحصائية.

الخطوة 3: تحليل المؤامرات المتبقية

يقدم الانحدار الخطي البسيط افتراضين مهمين حول بقايا النموذج:

• يتم توزيع البقايا بشكل طبيعي.
• البقايا لها تباين متساوي (” التجانس “) في كل مستوى من متغير التوقع.

إذا لم يتم استيفاء هذه الافتراضات، فإن نتائج نموذج الانحدار الخاص بنا قد لا تكون موثوقة.

للتحقق من استيفاء هذه الافتراضات، يمكننا تحليل المخططات المتبقية التي يعرضها SAS تلقائيًا في المخرجات:

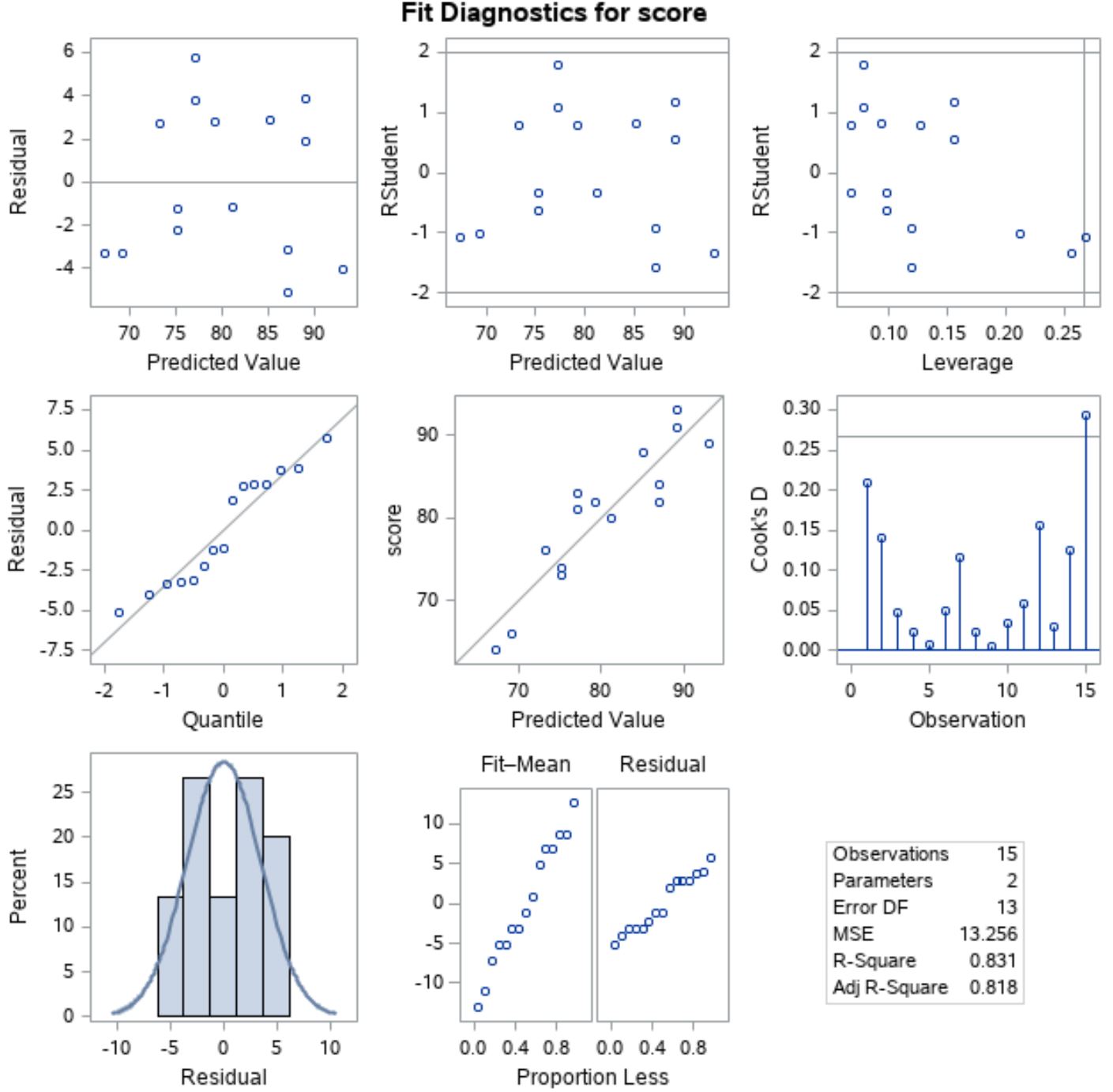
للتحقق من أن البقايا موزعة بشكل طبيعي ، يمكننا تحليل المؤامرة في الموضع الأيسر من الخط الأوسط مع “Quantile” على طول المحور x و “Residual” على طول المحور y.

يُطلق على هذا المخطط اسم مخطط QQ ، وهو اختصار لـ “الكمي الكمي”، ويستخدم لتحديد ما إذا كانت البيانات يتم توزيعها بشكل طبيعي أم لا. إذا تم توزيع البيانات بشكل طبيعي، فإن النقاط على مخطط QQ سوف تقع على خط قطري مستقيم.

من الرسم البياني يمكننا أن نرى أن النقاط تقع تقريبًا على طول خط قطري مستقيم، لذلك يمكننا أن نفترض أن البقايا يتم توزيعها بشكل طبيعي.

بعد ذلك، للتحقق من أن القيم المتبقية متجانسة ، يمكننا أن ننظر إلى المخطط في الموضع الأيسر من الصف الأول مع “القيمة المتوقعة” على طول المحور السيني و”المتبقي” على طول المحور الصادي.

إذا كانت نقاط الرسم متناثرة بشكل عشوائي حول الصفر بدون نمط واضح، فيمكننا أن نفترض أن البقايا متجانسة.

من الرسم يمكننا أن نرى أن النقاط متناثرة حول الصفر عشوائيا مع تباين متساو تقريبا عند كل مستوى في جميع أنحاء المخطط، لذلك يمكننا أن نفترض أن البقايا متجانسة.

وبما أن كلا الافتراضين قد تحققا، يمكننا أن نفترض أن نتائج نموذج الانحدار الخطي البسيط يمكن الاعتماد عليها.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في SAS:

كيفية إجراء ANOVA أحادي الاتجاه في SAS
كيفية إجراء ANOVA ثنائي الاتجاه في SAS
كيفية حساب الارتباط في SAS