كيفية إجراء الانحدار الخطي البسيط في لغة بايثون (خطوة بخطوة)

الانحدار الخطي البسيط هو أسلوب يمكننا استخدامه لفهم العلاقة بين متغير توضيحي واحد ومتغير استجابة واحد.

تعثر هذه التقنية على السطر الذي “يناسب” البيانات بشكل أفضل ويأخذ النموذج التالي:

ŷ = ب ₀ + ب ₁ س

ذهب:

• ŷ : قيمة الاستجابة المقدرة
• ب ₀ : أصل خط الانحدار
• ب ₁ : ميل خط الانحدار

يمكن أن تساعدنا هذه المعادلة في فهم العلاقة بين المتغير التوضيحي ومتغير الاستجابة و(على افتراض أنها ذات دلالة إحصائية) يمكن استخدامها للتنبؤ بقيمة متغير الاستجابة بالنظر إلى قيمة المتغير التوضيحي.

يقدم هذا البرنامج التعليمي شرحًا خطوة بخطوة حول كيفية تنفيذ الانحدار الخطي البسيط في بايثون.

الخطوة 1: تحميل البيانات

في هذا المثال، سنقوم بإنشاء مجموعة بيانات مزيفة تحتوي على المتغيرين التاليين لـ 15 طالبًا:

• إجمالي عدد الساعات المدروسة لبعض الامتحانات
• نتيجة الإمتحان

سنحاول ملاءمة نموذج الانحدار الخطي البسيط باستخدام الساعات كمتغير توضيحي ونتائج الفحص كمتغير الاستجابة.

يوضح الكود التالي كيفية إنشاء مجموعة البيانات المزيفة هذه في بايثون:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})
      

#view first six rows of dataset
df[0:6]

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81

الخطوة 2: تصور البيانات

قبل تركيب نموذج الانحدار الخطي البسيط، يجب علينا أولاً تصور البيانات لفهمها.

أولاً، نريد التأكد من أن العلاقة بين الساعات والنتيجة خطية تقريبًا، نظرًا لأن هذا هو الافتراض الأساسي للانحدار الخطي البسيط.

يمكننا إنشاء مخطط مبعثر بسيط لتصور العلاقة بين المتغيرين:

 import matplotlib.pyplot as plt

plt. scatter (df.hours, df.score)
plt. title (' Hours studied vs. Exam Score ')
plt. xlabel (' Hours ')
plt. ylabel (' Score ')
plt. show ()

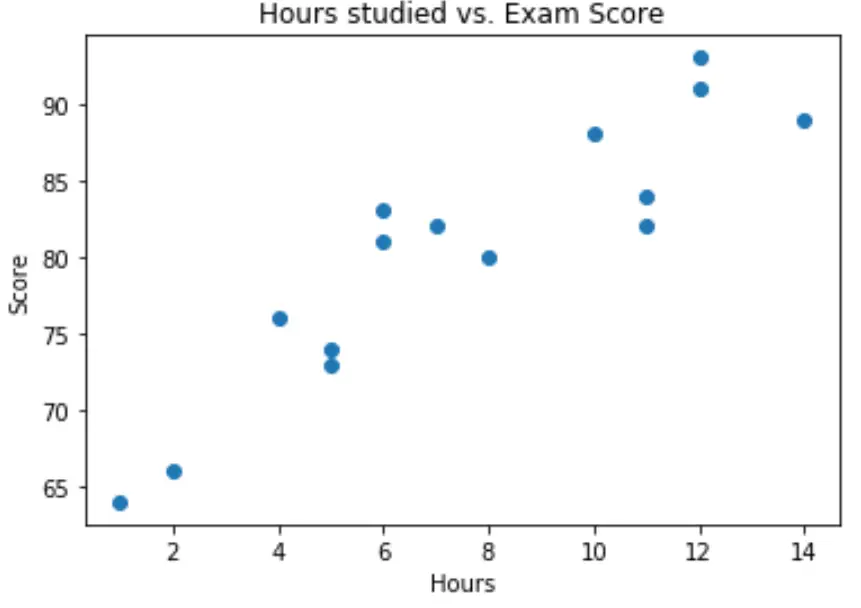
من الرسم البياني يمكننا أن نرى أن العلاقة تبدو خطية. مع زيادة عدد الساعات ، تميل النتيجة أيضًا إلى الزيادة خطيًا.

ثم يمكننا إنشاء مخطط boxplot لتصور توزيع نتائج الامتحانات والتحقق من القيم المتطرفة . افتراضيًا، تحدد بايثون الملاحظة على أنها قيمة متطرفة إذا كانت 1.5 مرة من النطاق الربيعي فوق الربع الثالث (Q3) أو 1.5 مرة من المدى الربيعي أسفل الربع الأول (Q1).

إذا كانت الملاحظة غريبة، فستظهر دائرة صغيرة في المخطط الصندوقي:

 df. boxplot (column=[' score ']) 

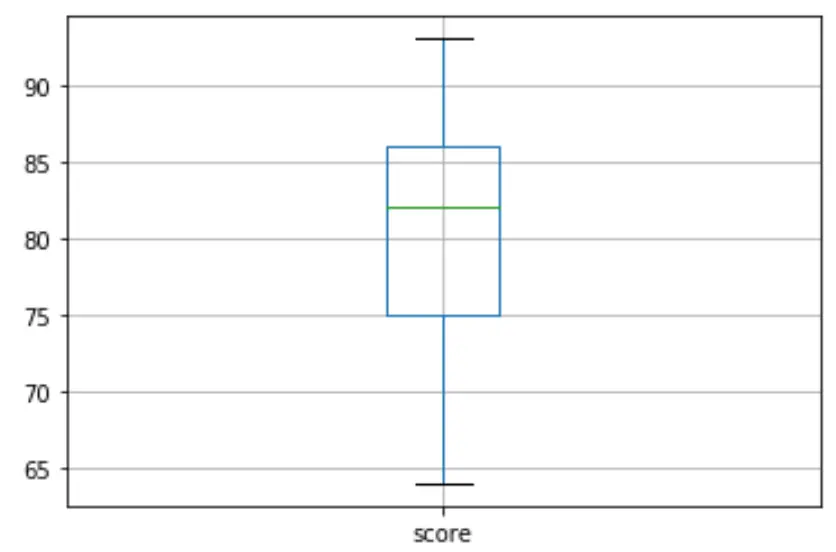
لا توجد دوائر صغيرة في boxplot، مما يعني عدم وجود قيم متطرفة في مجموعة البيانات لدينا.

الخطوة 3: إجراء الانحدار الخطي البسيط

بمجرد أن نتأكد من أن العلاقة بين متغيراتنا خطية ولا توجد قيم متطرفة، يمكننا المضي قدمًا لتناسب نموذج الانحدار الخطي البسيط باستخدام الساعات كمتغير توضيحي والنتيجة كمتغير استجابة:

ملاحظة: سوف نستخدم الدالة OLS() من مكتبة statsmodels لتناسب نموذج الانحدار.

 import statsmodels.api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06
Time: 15:51:45 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

ومن ملخص النموذج يمكننا أن نرى أن معادلة الانحدار المجهزة هي:

النتيجة = 65.334 + 1.9824*(ساعات)

وهذا يعني أن كل ساعة إضافية تتم دراستها ترتبط بزيادة في متوسط درجات الامتحان بمقدار 1.9824 نقطة. وتخبرنا القيمة الأصلية البالغة 65,334 بمتوسط درجات الاختبار المتوقعة للطالب الذي يدرس لمدة صفر ساعة.

يمكننا أيضًا استخدام هذه المعادلة للعثور على درجة الامتحان المتوقعة بناءً على عدد الساعات التي يدرسها الطالب. على سبيل المثال، الطالب الذي يدرس لمدة 10 ساعات يجب أن يحقق درجة الامتحان 85.158 :

النتيجة = 65.334 + 1.9824*(10) = 85.158

فيما يلي كيفية تفسير بقية ملخص النموذج:

• ف>|ر| : هذه هي القيمة p المرتبطة بمعاملات النموذج. وبما أن القيمة p للساعات (0.000) أقل بكثير من 0.05، يمكننا القول أن هناك علاقة ذات دلالة إحصائية بين الساعات والنتيجة .
• R-squared: يخبرنا هذا الرقم أن نسبة التباين في درجات الامتحان يمكن تفسيرها بعدد الساعات المدروسة. بشكل عام، كلما زادت قيمة R-squared لنموذج الانحدار، كلما كانت المتغيرات التوضيحية قادرة على التنبؤ بقيمة متغير الاستجابة بشكل أفضل. في هذه الحالة، يتم تفسير 83.1% من التباين في الدرجات من خلال ساعات الدراسة.
• إحصائية F وقيمة p: تخبرنا إحصائية F ( 63.91 ) والقيمة p المقابلة ( 2.25e-06 ) بالأهمية الإجمالية لنموذج الانحدار، أي ما إذا كانت المتغيرات التوضيحية في النموذج مفيدة في تفسير التباين . في متغير الاستجابة نظرًا لأن القيمة p في هذا المثال أقل من 0.05، فإن نموذجنا ذو دلالة إحصائية وتعتبر الساعات مفيدة في شرح تباين النتيجة .

الخطوة 4: إنشاء قطع الأراضي المتبقية

بعد ملائمة نموذج الانحدار الخطي البسيط للبيانات، فإن الخطوة الأخيرة هي إنشاء مخططات متبقية.

أحد الافتراضات الرئيسية للانحدار الخطي هو أن بقايا نموذج الانحدار يتم توزيعها بشكل طبيعي تقريبًا وتكون متجانسة عند كل مستوى من مستويات المتغير التوضيحي. إذا لم يتم استيفاء هذه الافتراضات، فقد تكون نتائج نموذج الانحدار الخاص بنا مضللة أو غير موثوقة.

وللتحقق من استيفاء هذه الافتراضات، يمكننا إنشاء المخططات المتبقية التالية:

مخطط القيم المتبقية مقابل القيم المجهزة: هذا المخطط مفيد لتأكيد المثلية. يعرض المحور السيني القيم المجهزة ويعرض المحور الصادي القيم المتبقية. وطالما أن البقايا تبدو موزعة بشكل عشوائي وموحد في جميع أنحاء الرسم البياني حول القيمة الصفرية، يمكننا أن نفترض أن المثلية لم تنتهك:

 #define figure size
fig = plt. figure (figsize=(12.8))

#produce residual plots
fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)

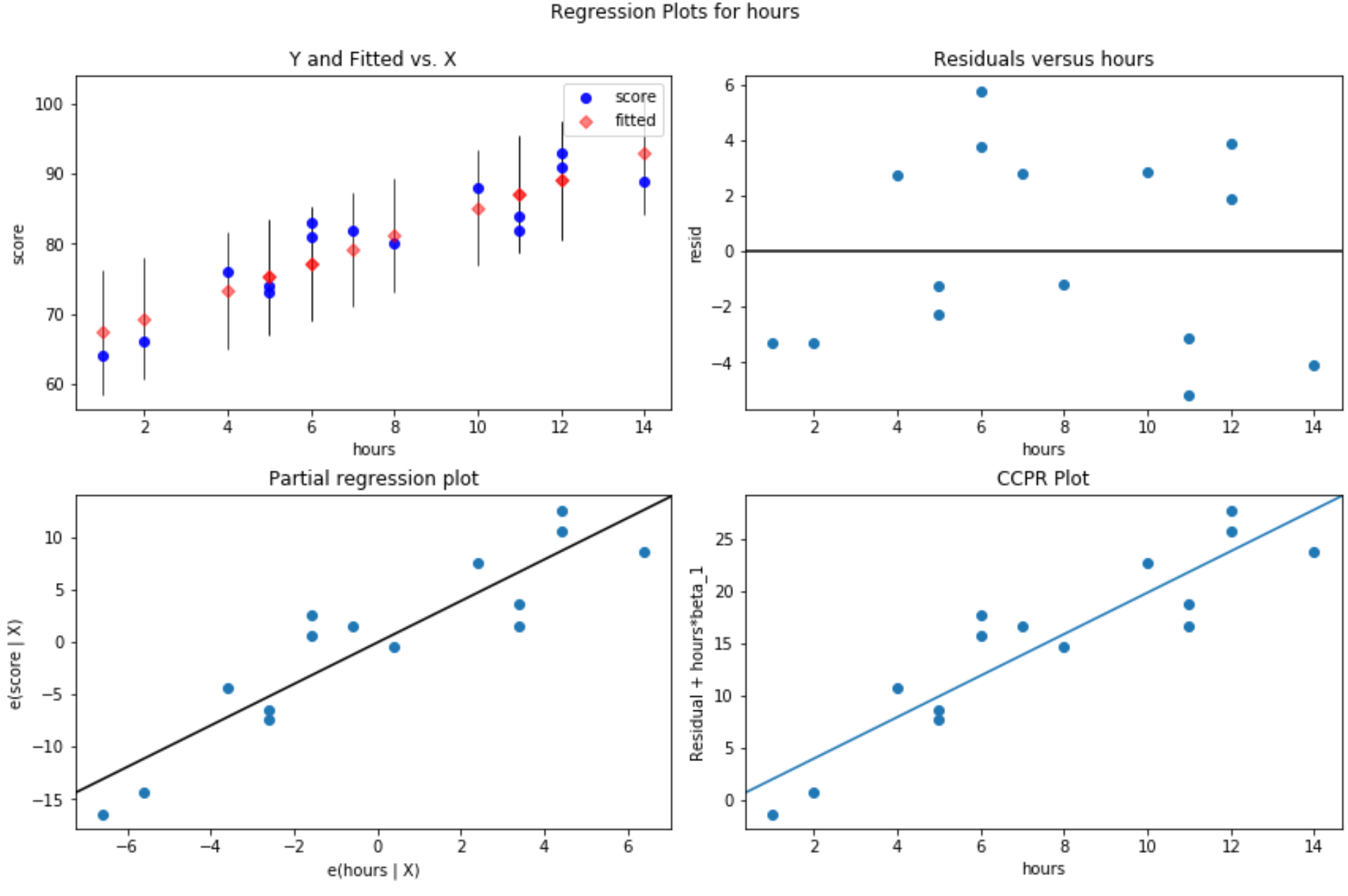
يتم إنتاج أربع قطع. القطعة الموجودة في الزاوية اليمنى العليا هي قطعة الأرض المتبقية مقابل قطعة الأرض المعدلة. يُظهر المحور السيني في هذا الرسم القيم الفعلية لنقاط متغير التوقع ويظهر المحور الصادي المتبقي لتلك القيمة.

وبما أن البقايا تبدو منتشرة بشكل عشوائي حول الصفر، فهذا يشير إلى أن التغايرية ليست مشكلة في المتغير التوضيحي.

مؤامرة QQ: هذه المؤامرة مفيدة لتحديد ما إذا كانت البقايا تتبع التوزيع الطبيعي. إذا كانت قيم البيانات في المخطط تتبع خطًا مستقيمًا تقريبًا بزاوية 45 درجة، فسيتم توزيع البيانات بشكل طبيعي:

 #define residuals
res = model. reside

#create QQ plot
fig = sm. qqplot (res, fit= True , line=" 45 ")
plt.show() 

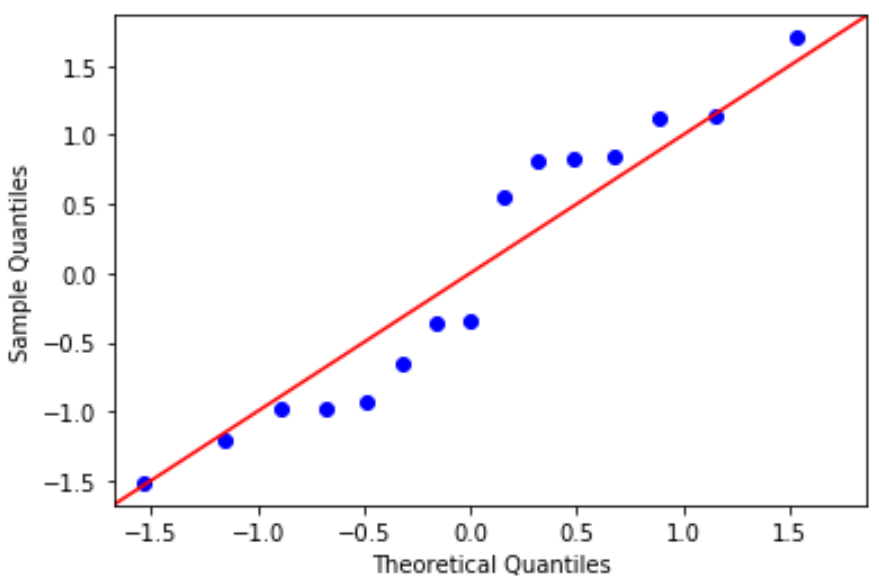
تنحرف البقايا قليلاً عن خط 45 درجة، لكن ليس بما يكفي لإثارة قلق بالغ. يمكننا أن نفترض أن افتراض الحالة الطبيعية قد تم استيفاءه.

وبما أن البقايا موزعة بشكل طبيعي ومتجانسة، فقد تحققنا من استيفاء فرضيات نموذج الانحدار الخطي البسيط. وبالتالي، فإن مخرجات نموذجنا موثوقة.

يمكن العثور على كود Python الكامل المستخدم في هذا البرنامج التعليمي هنا .