كيفية تنفيذ الانحدار الخطي البسيط في r (خطوة بخطوة)

الانحدار الخطي البسيط هو أسلوب يمكننا استخدامه لفهم العلاقة بين متغير توضيحي واحد ومتغير استجابة واحد.

باختصار، تقوم هذه التقنية بإيجاد السطر الذي “يناسب” البيانات بشكل أفضل ويأخذ النموذج التالي:

ŷ = ب ₀ + ب ₁ س

ذهب:

• ŷ : قيمة الاستجابة المقدرة
• ب ₀ : أصل خط الانحدار
• ب ₁ : ميل خط الانحدار

يمكن أن تساعدنا هذه المعادلة في فهم العلاقة بين المتغير التوضيحي ومتغير الاستجابة و(على افتراض أنها ذات دلالة إحصائية) يمكن استخدامها للتنبؤ بقيمة متغير الاستجابة بالنظر إلى قيمة المتغير التوضيحي.

يقدم هذا البرنامج التعليمي شرحًا خطوة بخطوة لكيفية إجراء الانحدار الخطي البسيط في R.

الخطوة 1: تحميل البيانات

في هذا المثال، سنقوم بإنشاء مجموعة بيانات مزيفة تحتوي على المتغيرين التاليين لـ 15 طالبًا:

• إجمالي عدد الساعات المدروسة لبعض الامتحانات
• نتيجة الإمتحان

سنحاول ملاءمة نموذج الانحدار الخطي البسيط باستخدام الساعات كمتغير توضيحي ونتائج الفحص كمتغير الاستجابة.

يوضح الكود التالي كيفية إنشاء مجموعة البيانات المزيفة هذه في R:

 #create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

#attach dataset to make it more convenient to work with
attach(df)

الخطوة 2: تصور البيانات

قبل تركيب نموذج الانحدار الخطي البسيط، يجب علينا أولاً تصور البيانات لفهمها.

أولاً، نريد التأكد من أن العلاقة بين الساعات والنتيجة خطية تقريبًا، نظرًا لأن هذا افتراض أساسي كبير للانحدار الخطي البسيط. يمكننا إنشاء مخطط مبعثر بسيط لتصور العلاقة بين المتغيرين:

 scatter.smooth(hours, score, main=' Hours studied vs. Exam Score ')

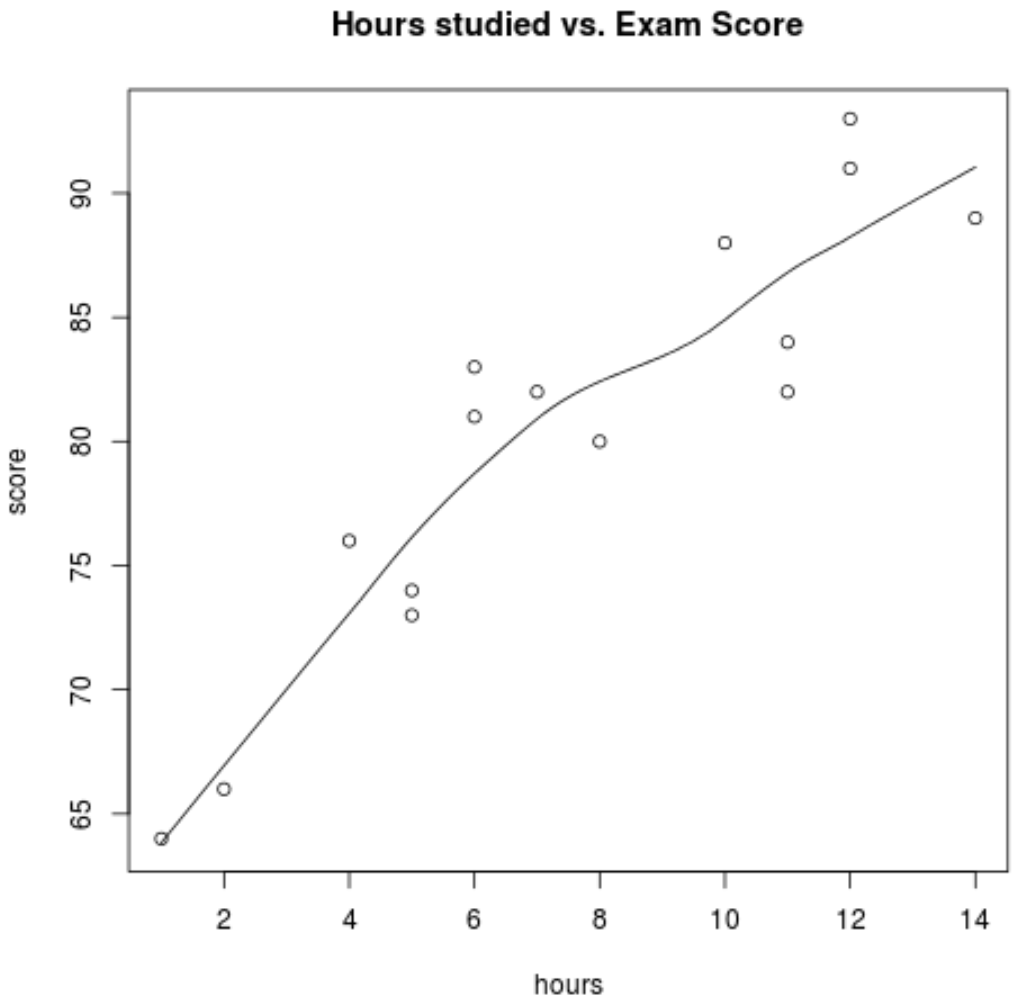
من الرسم البياني يمكننا أن نرى أن العلاقة تبدو خطية. مع زيادة عدد الساعات ، تميل النتيجة أيضًا إلى الزيادة خطيًا.

ثم يمكننا إنشاء مخطط boxplot لتصور توزيع نتائج الامتحانات والتحقق من القيم المتطرفة . افتراضيًا، يُعرّف R الملاحظة على أنها قيمة متطرفة إذا كانت 1.5 مرة من المدى الربيعي فوق الربع الثالث (Q3) أو 1.5 مرة من المدى الربيعي أسفل الربيع الأول (Q1).

إذا كانت الملاحظة غريبة، فستظهر دائرة صغيرة في المخطط الصندوقي:

 boxplot(score) 

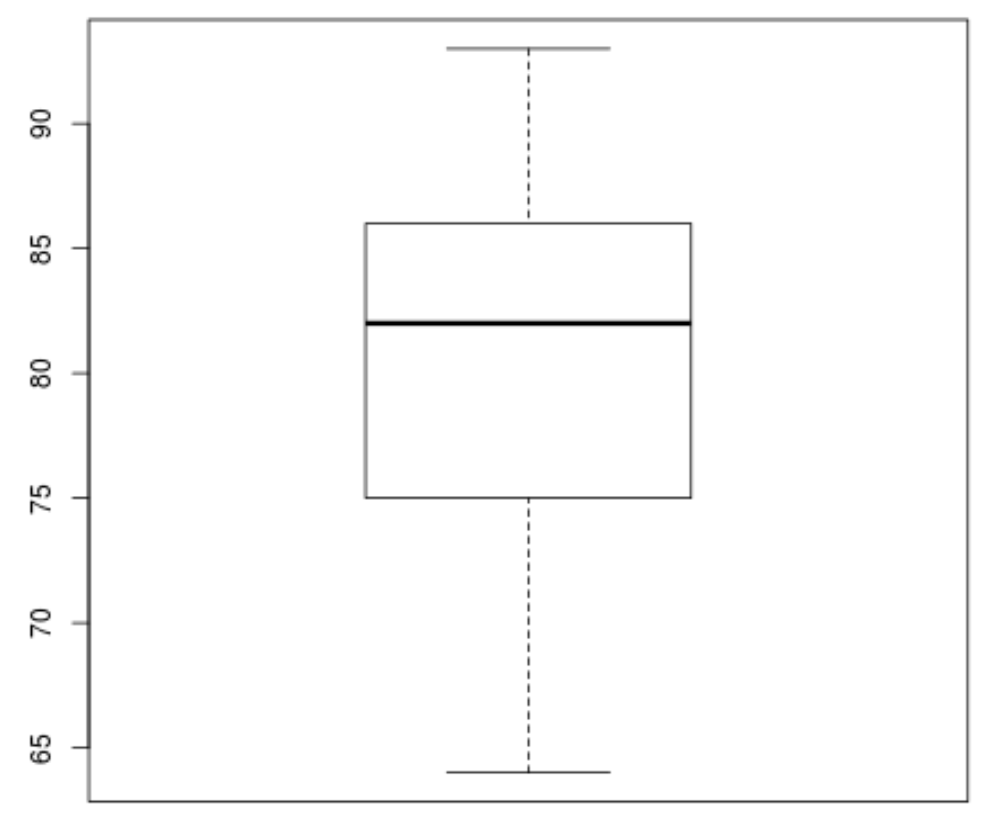
لا توجد دوائر صغيرة في boxplot، مما يعني عدم وجود قيم متطرفة في مجموعة البيانات لدينا.

الخطوة 3: إجراء الانحدار الخطي البسيط

بمجرد أن نتأكد من أن العلاقة بين متغيراتنا خطية ولا توجد قيم متطرفة، يمكننا المضي قدمًا لتناسب نموذج الانحدار الخطي البسيط باستخدام الساعات كمتغير توضيحي والنتيجة كمتغير استجابة:

 #fit simple linear regression model
model <- lm(score~hours)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

ومن ملخص النموذج يمكننا أن نرى أن معادلة الانحدار المجهزة هي:

النتيجة = 65.334 + 1.982*(ساعات)

وهذا يعني أن كل ساعة إضافية تتم دراستها ترتبط بزيادة في متوسط درجات الامتحان قدرها 1982 نقطة. وتخبرنا القيمة الأصلية البالغة 65,334 بمتوسط درجات الاختبار المتوقعة للطالب الذي يدرس لمدة صفر ساعة.

يمكننا أيضًا استخدام هذه المعادلة للعثور على درجة الامتحان المتوقعة بناءً على عدد الساعات التي يدرسها الطالب. على سبيل المثال، الطالب الذي يدرس لمدة 10 ساعات يجب أن يحقق درجة الامتحان 85.15 :

النتيجة = 65.334 + 1.982*(10) = 85.15

فيما يلي كيفية تفسير بقية ملخص النموذج:

• Pr(>|t|): هذه هي القيمة p المرتبطة بمعاملات النموذج. وبما أن القيمة p للساعات (2.25e-06) أقل بكثير من 0.05، فيمكننا القول أن هناك ارتباطًا ذو دلالة إحصائية بين الساعات والنتيجة .
• مضاعف R-squared: يخبرنا هذا الرقم أن نسبة التباين في درجات الامتحان يمكن تفسيرها بعدد ساعات الدراسة. بشكل عام، كلما زادت قيمة R-squared لنموذج الانحدار، كلما كانت المتغيرات التوضيحية قادرة على التنبؤ بقيمة متغير الاستجابة بشكل أفضل. في هذه الحالة، يمكن تفسير 83.1% من التباين في الدرجات من خلال ساعات الدراسة.
• الخطأ المعياري المتبقي: هذا هو متوسط المسافة بين القيم المرصودة وخط الانحدار. كلما انخفضت هذه القيمة، زادت قدرة خط الانحدار على التوافق مع البيانات المرصودة. في هذه الحالة، ينحرف متوسط الدرجات المسجلة في الاختبار بمقدار 3641 نقطة عن الدرجة المتوقعة بواسطة خط الانحدار.
• إحصائية F وقيمة p: تخبرنا إحصائية F ( 63.91 ) والقيمة p المقابلة لها ( 2.253e-06 ) بالأهمية الإجمالية لنموذج الانحدار، أي ما إذا كانت المتغيرات التوضيحية في النموذج مفيدة لشرح التباين . في متغير الاستجابة نظرًا لأن القيمة p في هذا المثال أقل من 0.05، فإن نموذجنا ذو دلالة إحصائية وتعتبر الساعات مفيدة في شرح تباين النتيجة .

الخطوة 4: إنشاء قطع الأراضي المتبقية

بعد ملائمة نموذج الانحدار الخطي البسيط للبيانات، فإن الخطوة الأخيرة هي إنشاء مخططات متبقية.

أحد الافتراضات الرئيسية للانحدار الخطي هو أن بقايا نموذج الانحدار يتم توزيعها بشكل طبيعي تقريبًا وتكون متجانسة عند كل مستوى من مستويات المتغير التوضيحي. إذا لم يتم استيفاء هذه الافتراضات، فقد تكون نتائج نموذج الانحدار الخاص بنا مضللة أو غير موثوقة.

وللتحقق من استيفاء هذه الافتراضات، يمكننا إنشاء المخططات المتبقية التالية:

مخطط القيم المتبقية مقابل القيم المجهزة: هذا المخطط مفيد لتأكيد المثلية. يعرض المحور السيني القيم المجهزة ويعرض المحور الصادي القيم المتبقية. وطالما أن البقايا تبدو موزعة بشكل عشوائي وموحد في جميع أنحاء الرسم البياني حول القيمة الصفرية، يمكننا أن نفترض أن المثلية لم تنتهك:

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

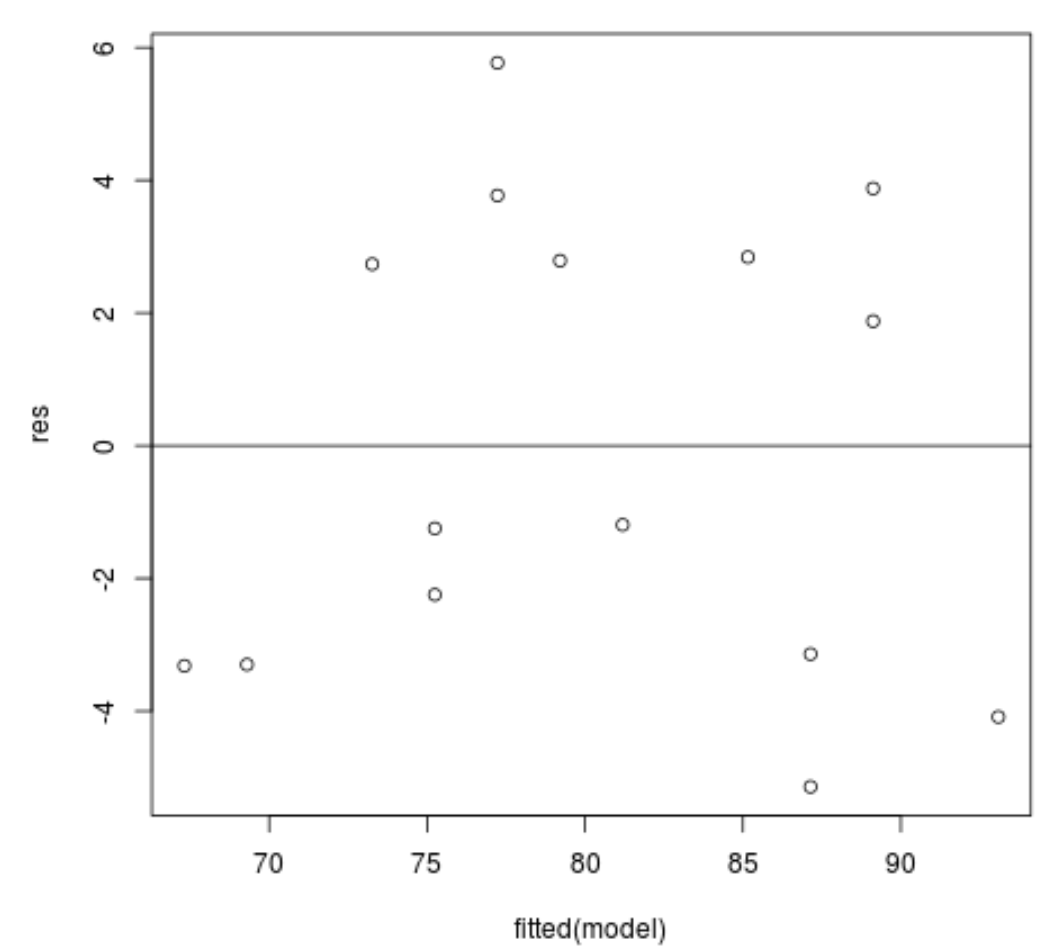
ويبدو أن البقايا متناثرة بشكل عشوائي حول الصفر ولا تظهر أي نمط ملحوظ، لذلك تم تحقيق هذا الافتراض.

مؤامرة QQ: هذه المؤامرة مفيدة لتحديد ما إذا كانت البقايا تتبع التوزيع الطبيعي. إذا كانت قيم البيانات في المخطط تتبع خطًا مستقيمًا تقريبًا بزاوية 45 درجة، فسيتم توزيع البيانات بشكل طبيعي:

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

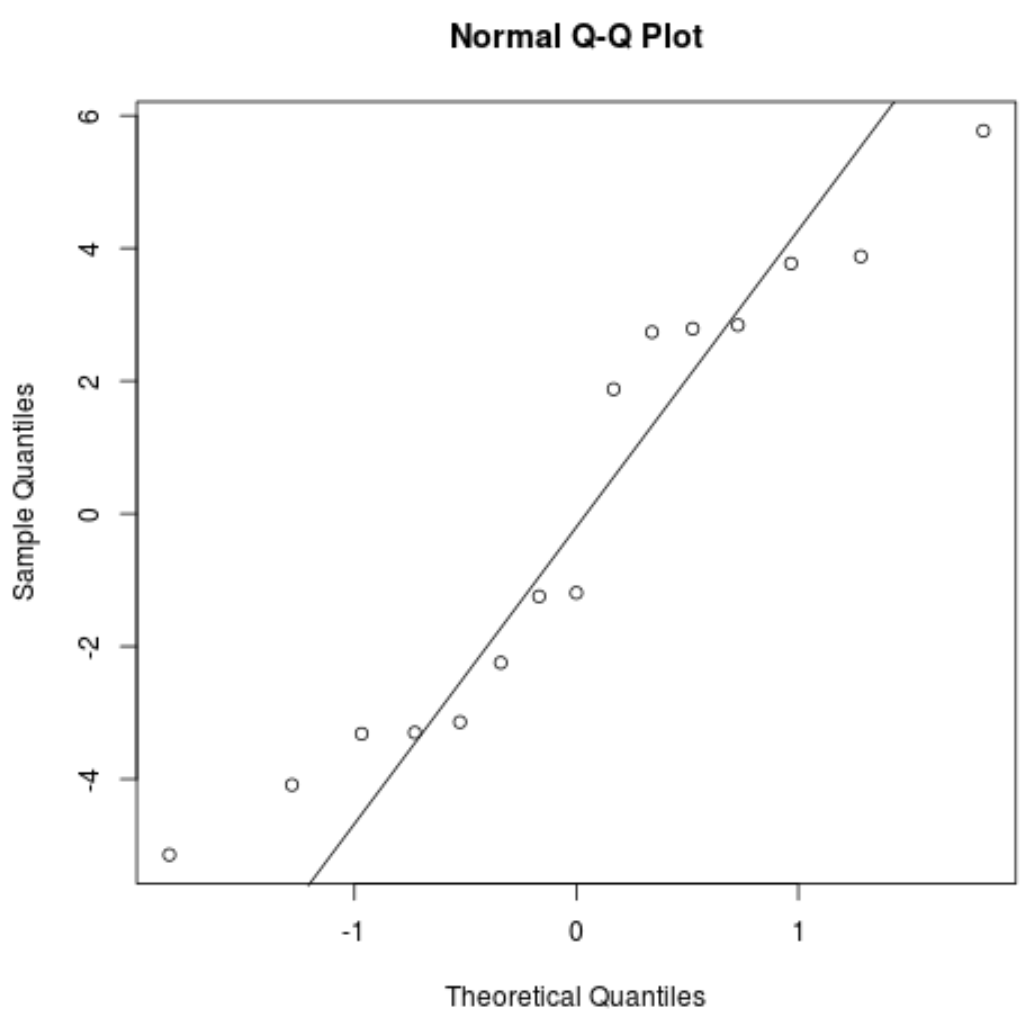
تنحرف البقايا قليلاً عن خط 45 درجة، لكن ليس بما يكفي لإثارة قلق بالغ. يمكننا أن نفترض أن افتراض الحالة الطبيعية قد تم استيفاءه.

وبما أن البقايا موزعة بشكل طبيعي ومتجانسة، فقد تحققنا من استيفاء فرضيات نموذج الانحدار الخطي البسيط. وبالتالي، فإن مخرجات نموذجنا موثوقة.

يمكن العثور على رمز R الكامل المستخدم في هذا البرنامج التعليمي هنا .