كيفية إجراء الانحدار الخطي المتعدد في spss

الانحدار الخطي المتعدد هو طريقة يمكننا استخدامها لفهم العلاقة بين متغيرين توضيحيين أو أكثر ومتغير الاستجابة.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار الخطي المتعدد في برنامج SPSS.

مثال: الانحدار الخطي المتعدد في برنامج SPSS

لنفترض أننا نريد معرفة ما إذا كان عدد الساعات التي يقضيها في الدراسة وعدد الاختبارات التدريبية التي تم إجراؤها يؤثر على الدرجة التي يحصل عليها الطالب في اختبار معين. لاستكشاف ذلك، يمكننا إجراء الانحدار الخطي المتعدد باستخدام المتغيرات التالية:

المتغيرات التوضيحية:

• ساعات الدراسة
• تم اجتياز الامتحانات التحضيرية

متغير استجابة:

• نتيجة الإمتحان

استخدم الخطوات التالية لتنفيذ هذا الانحدار الخطي المتعدد في SPSS.

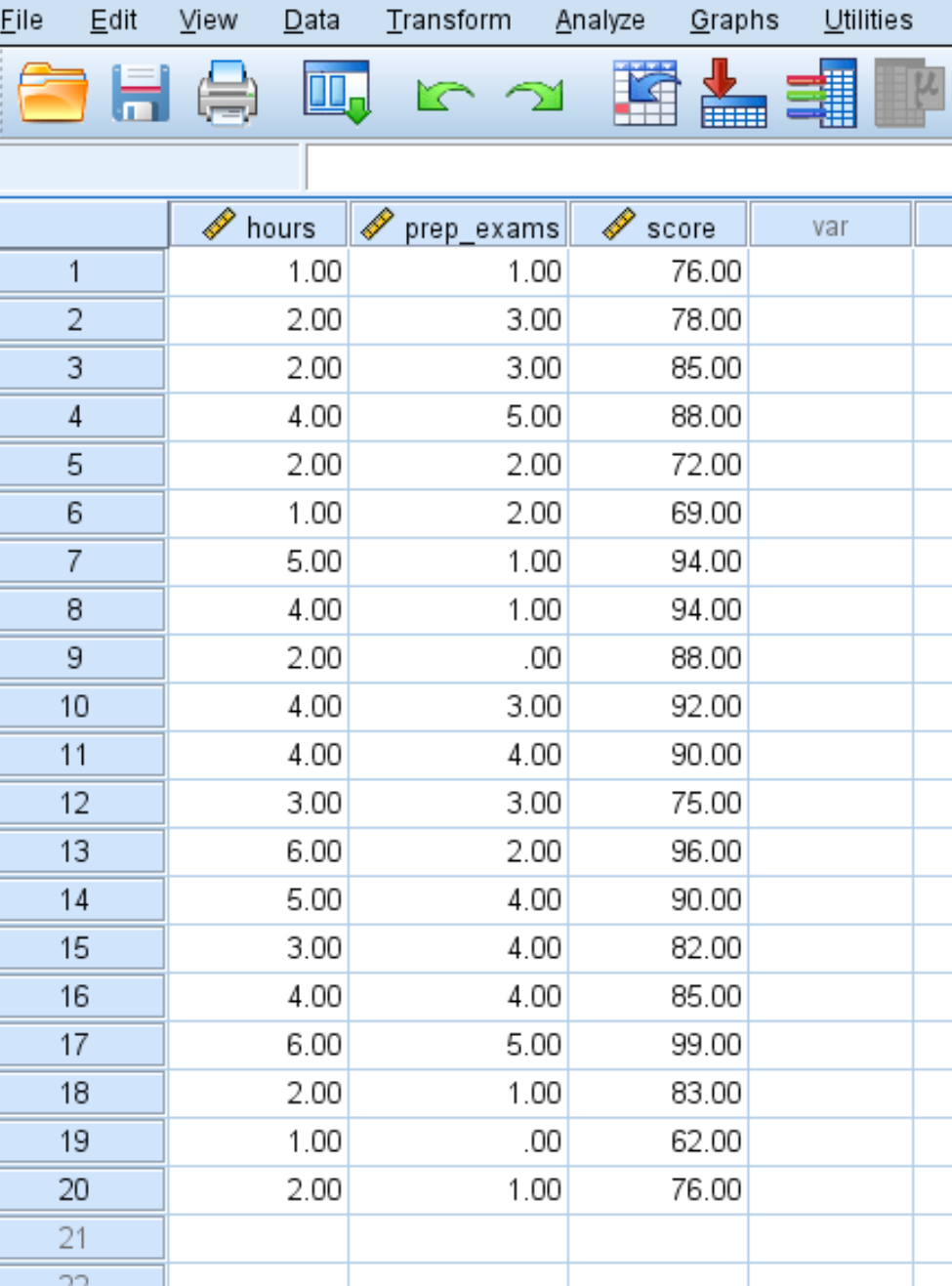
الخطوة 1: أدخل البيانات.

أدخل البيانات التالية لعدد الساعات المدروسة والاختبارات الإعدادية ونتائج الامتحانات الواردة لـ 20 طالباً:

الخطوة 2: تنفيذ الانحدار الخطي المتعدد.

انقر فوق علامة التبويب تحليل ، ثم الانحدار ، ثم الخطي :

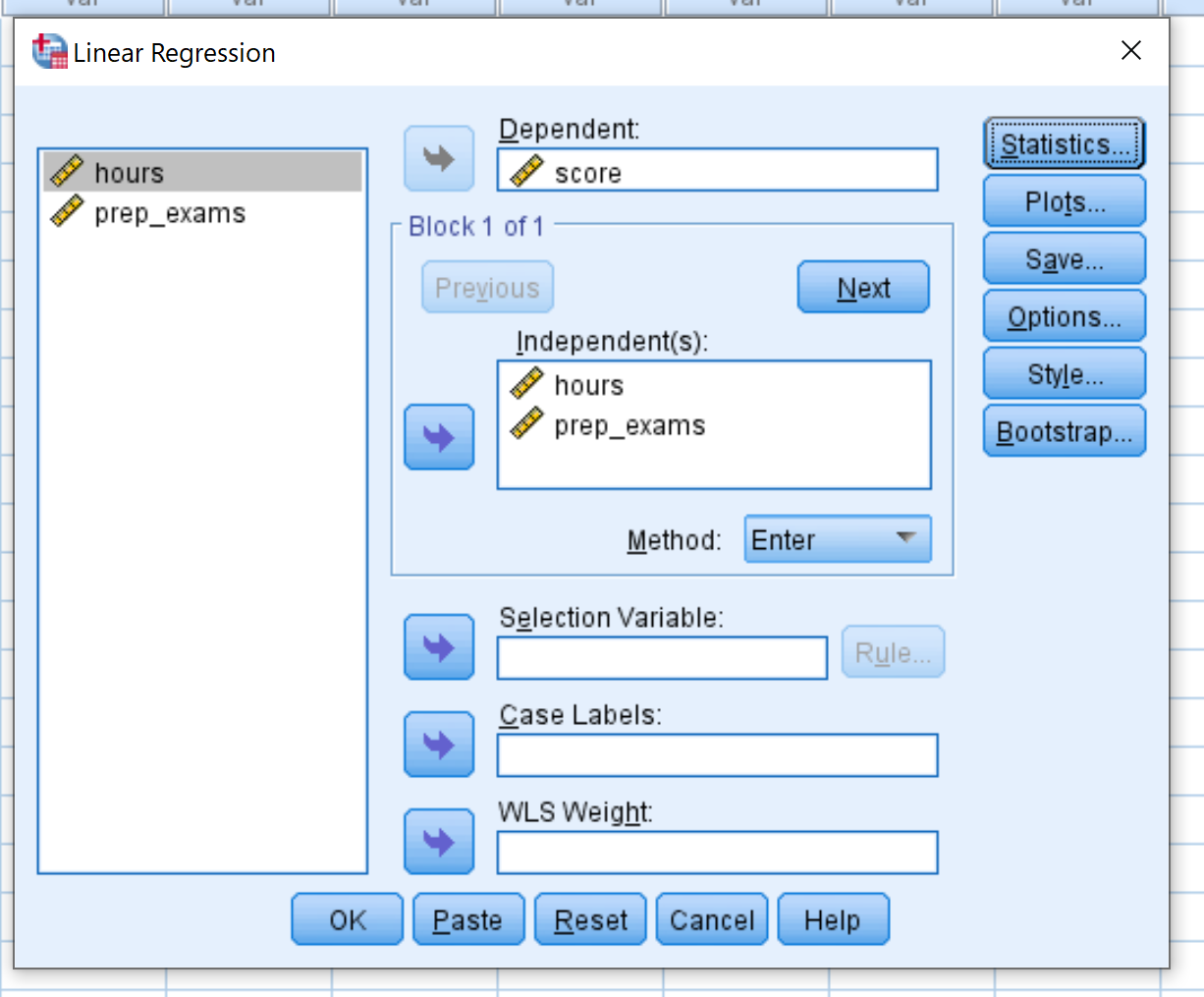
اسحب النتيجة المتغيرة إلى المربع المسمى “تابع”. اسحب متغيرات الساعات و prep_exams إلى المربع المسمى المستقل (المستقلون). ثم انقر فوق موافق .

الخطوة 3: تفسير النتيجة.

بمجرد النقر فوق “موافق” ، ستظهر نتائج الانحدار الخطي المتعدد في نافذة جديدة.

الجدول الأول الذي يهمنا يسمى ملخص النموذج :

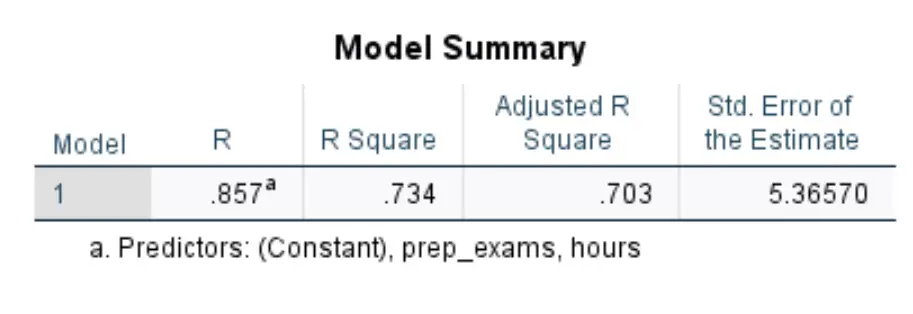
فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• مربع R: هو نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بالمتغيرات التوضيحية. في هذا المثال، يمكن تفسير 73.4% من التباين في درجات الامتحانات من خلال ساعات الدراسة وعدد الاختبارات الإعدادية التي تم إجراؤها.
• معيار. خطأ التقدير: الخطأ القياسي هو متوسط المسافة بين القيم المرصودة وخط الانحدار. في هذا المثال، تنحرف القيم المرصودة في المتوسط بمقدار 5.3657 وحدة عن خط الانحدار.

الجدول التالي الذي يهمنا يسمى ANOVA :

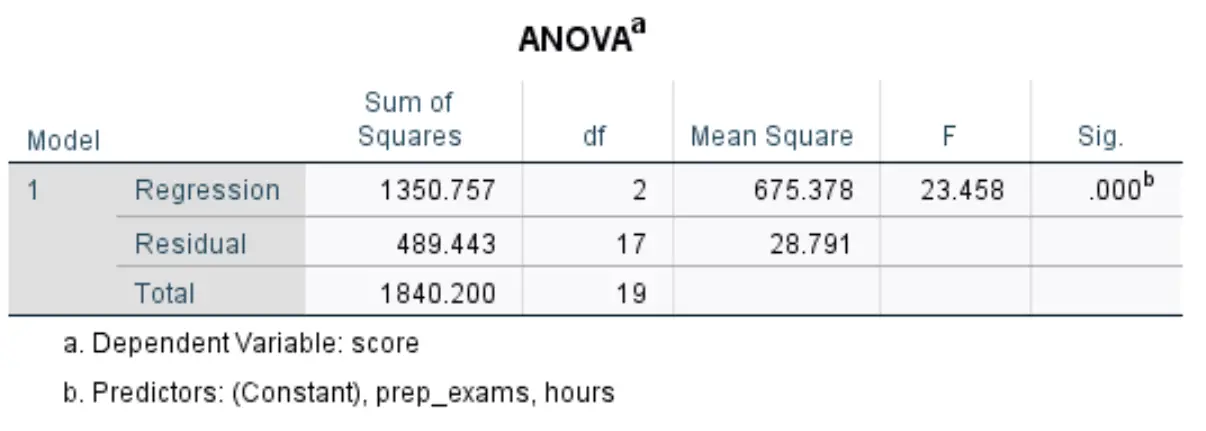
فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• F: هذه هي إحصائية F الإجمالية لنموذج الانحدار، ويتم حسابها على أنها متوسط مربع الانحدار / متوسط المربع المتبقي.
• Sig: هذه هي القيمة p المرتبطة بإحصائيات F الإجمالية. يخبرنا هذا ما إذا كان نموذج الانحدار ككل ذو دلالة إحصائية أم لا. وبعبارة أخرى، فإنه يخبرنا ما إذا كان المتغيران التوضيحيان مجتمعان لهما ارتباط ذو دلالة إحصائية مع متغير الاستجابة. وفي هذه الحالة تكون القيمة p تساوي 0.000، مما يدل على أن المتغيرات التوضيحية وساعات الدراسة والاختبارات التحضيرية التي تم إجراؤها، لها علاقة ذات دلالة إحصائية بنتيجة الامتحان.

الجدول التالي الذي يهمنا هو بعنوان المعاملات :

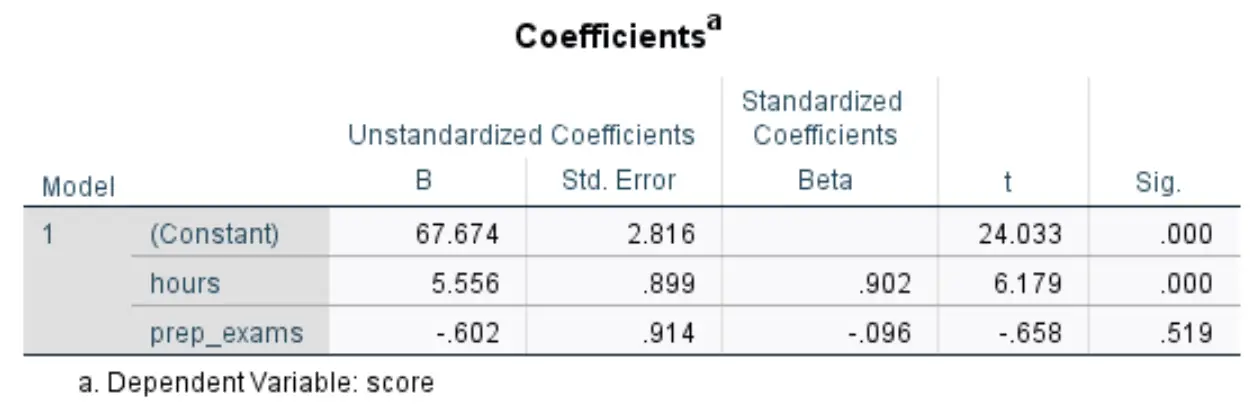
فيما يلي كيفية تفسير الأرقام الأكثر صلة في هذا الجدول:

• B غير قياسي (ثابت): يخبرنا هذا بالقيمة المتوسطة لمتغير الاستجابة عندما يكون كلا المتغيرين المتنبئين صفراً. في هذا المثال، متوسط درجات الامتحان هو 67,674 عندما تكون ساعات الدراسة والاختبارات التحضيرية صفرًا.
• غير قياسي B (ساعات): يخبرنا هذا بمتوسط التغير في درجات الامتحانات المرتبطة بزيادة وحدة واحدة في ساعات الدراسة، على افتراض أن عدد الاختبارات الإعدادية التي تم إجراؤها يظل ثابتًا. في هذه الحالة، ترتبط كل ساعة إضافية تقضيها في الدراسة بزيادة قدرها 5556 نقطة في درجة الاختبار، على افتراض أن عدد الاختبارات التدريبية التي تم إجراؤها يظل ثابتًا.
• غير قياسي B (prep_exams): يخبرنا هذا بمتوسط التغير في درجة الامتحان المرتبط بزيادة وحدة واحدة في الاختبارات الإعدادية التي يتم إجراؤها، على افتراض أن عدد ساعات الدراسة يظل ثابتًا. وفي هذه الحالة، يرتبط كل امتحان تحضيري إضافي يتم إجراؤه بانخفاض قدره 0.602 نقطة في درجة الامتحان، على افتراض بقاء عدد الساعات المدروسة ثابتا.
• سيج. (ساعات): هذه هي القيمة p للمتغير التوضيحي للساعات . وبما أن هذه القيمة (0.000) أقل من 0.05 فيمكننا أن نستنتج أن ساعات الدراسة لها علاقة ذات دلالة إحصائية مع درجات الامتحانات.
• سيج. (prep_exams): هذه هي القيمة p للمتغير التوضيحي prep_exams . وبما أن هذه القيمة (0.519) لا تقل عن 0.05، فلا يمكننا أن نستنتج أن عدد الاختبارات التحضيرية التي تم إجراؤها لها علاقة ذات دلالة إحصائية بنتيجة الامتحان.

وأخيراً يمكننا تكوين معادلة انحدار باستخدام القيم الموضحة في جدول الثابت والساعات والاختبارات الإعدادية . وفي هذه الحالة ستكون المعادلة:

درجة الاختبار المقدرة = 67.674 + 5.556*(ساعات) – 0.602*(امتحانات الإعدادية)

يمكننا استخدام هذه المعادلة للعثور على درجة الامتحان المقدرة للطالب، بناءً على عدد ساعات الدراسة وعدد الاختبارات التدريبية التي أجراها. على سبيل المثال، الطالب الذي يدرس لمدة 3 ساعات ويأخذ امتحانين إعداديين يجب أن يحصل على درجة الامتحان 83.1:

درجة الاختبار المقدرة = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

ملحوظة: بما أن المتغير التوضيحي للامتحانات الإعدادية لم يتبين أنه ذو دلالة إحصائية، يمكننا أن نقرر إزالته من النموذج وإجراء انحدار خطي بسيط بدلاً من ذلك باستخدام ساعات الدراسة باعتبارها المتغير التوضيحي الوحيد.