كيفية تنفيذ الانحدار الخطي المتعدد في إكسيل
الانحدار الخطي المتعدد هو أسلوب يمكننا استخدامه لفهم العلاقة بين متغيرين توضيحيين أو أكثر ومتغير الاستجابة .
يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار الخطي المتعدد في Excel.
ملاحظة: إذا كان لديك متغير توضيحي واحد فقط، فيجب عليك إجراء انحدار خطي بسيط بدلاً من ذلك.
مثال: الانحدار الخطي المتعدد في Excel
لنفترض أننا نريد معرفة ما إذا كان عدد الساعات التي يقضيها في الدراسة وعدد الاختبارات الإعدادية التي تم إجراؤها يؤثر على الدرجة التي يحصل عليها الطالب في امتحان دخول جامعي معين.
لاستكشاف هذه العلاقة، يمكننا إجراء الانحدار الخطي المتعدد باستخدام ساعات الدراسة والامتحانات التحضيرية التي يتم إجراؤها كمتغيرات توضيحية ونتائج الامتحانات كمتغير الاستجابة.
أكمل الخطوات التالية في Excel لإجراء انحدار خطي متعدد.
الخطوة 1: أدخل البيانات.
أدخل البيانات التالية لعدد الساعات المدروسة والاختبارات الإعدادية ونتائج الامتحانات الواردة لـ 20 طالباً:
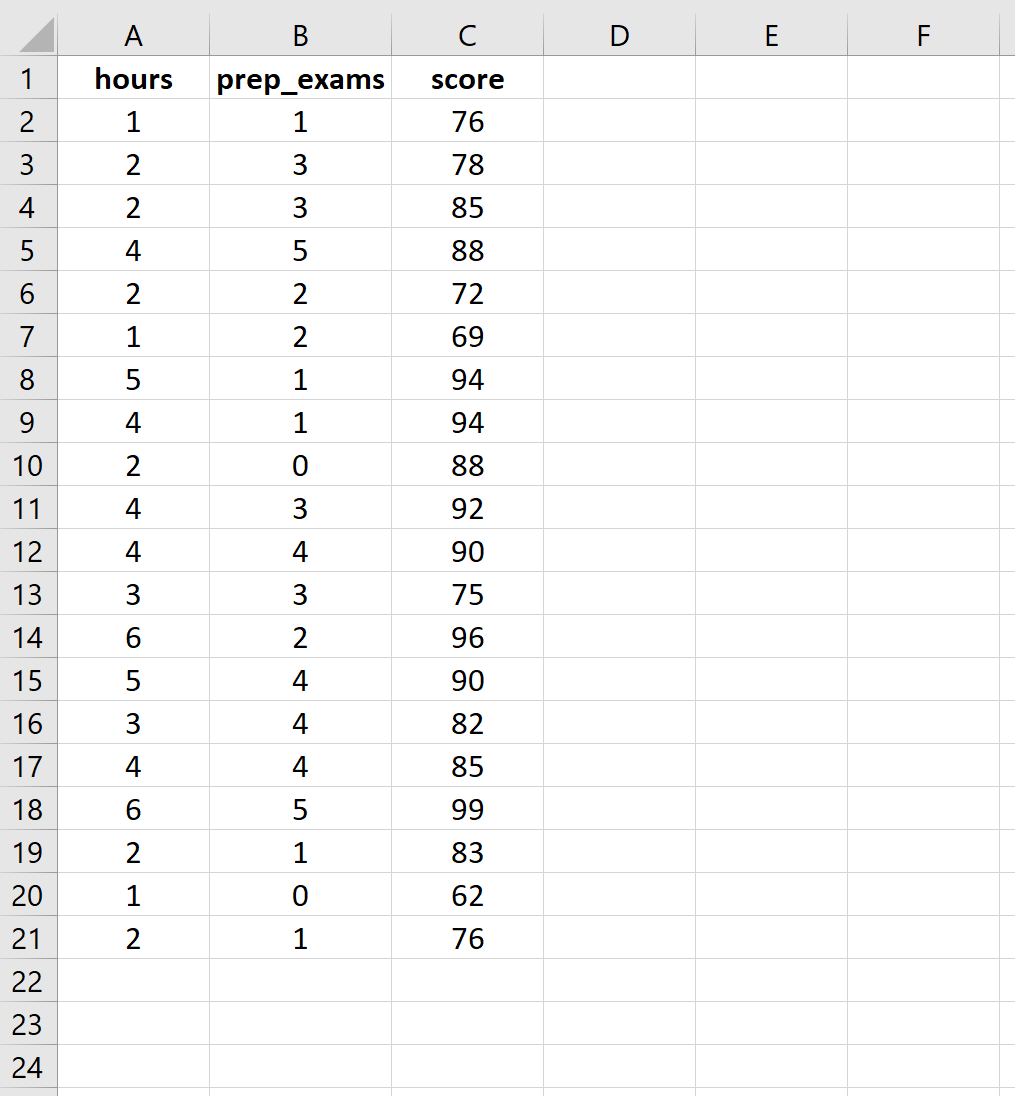
الخطوة 2: تنفيذ الانحدار الخطي المتعدد.
في الشريط العلوي لبرنامج Excel، انتقل إلى علامة التبويب “البيانات” وانقر فوق “تحليل البيانات” . إذا لم تشاهد هذا الخيار، فيجب عليك أولاً تثبيت برنامج Analysis ToolPak المجاني .
بمجرد النقر على تحليل البيانات، ستظهر نافذة جديدة. حدد الانحدار وانقر فوق موافق.
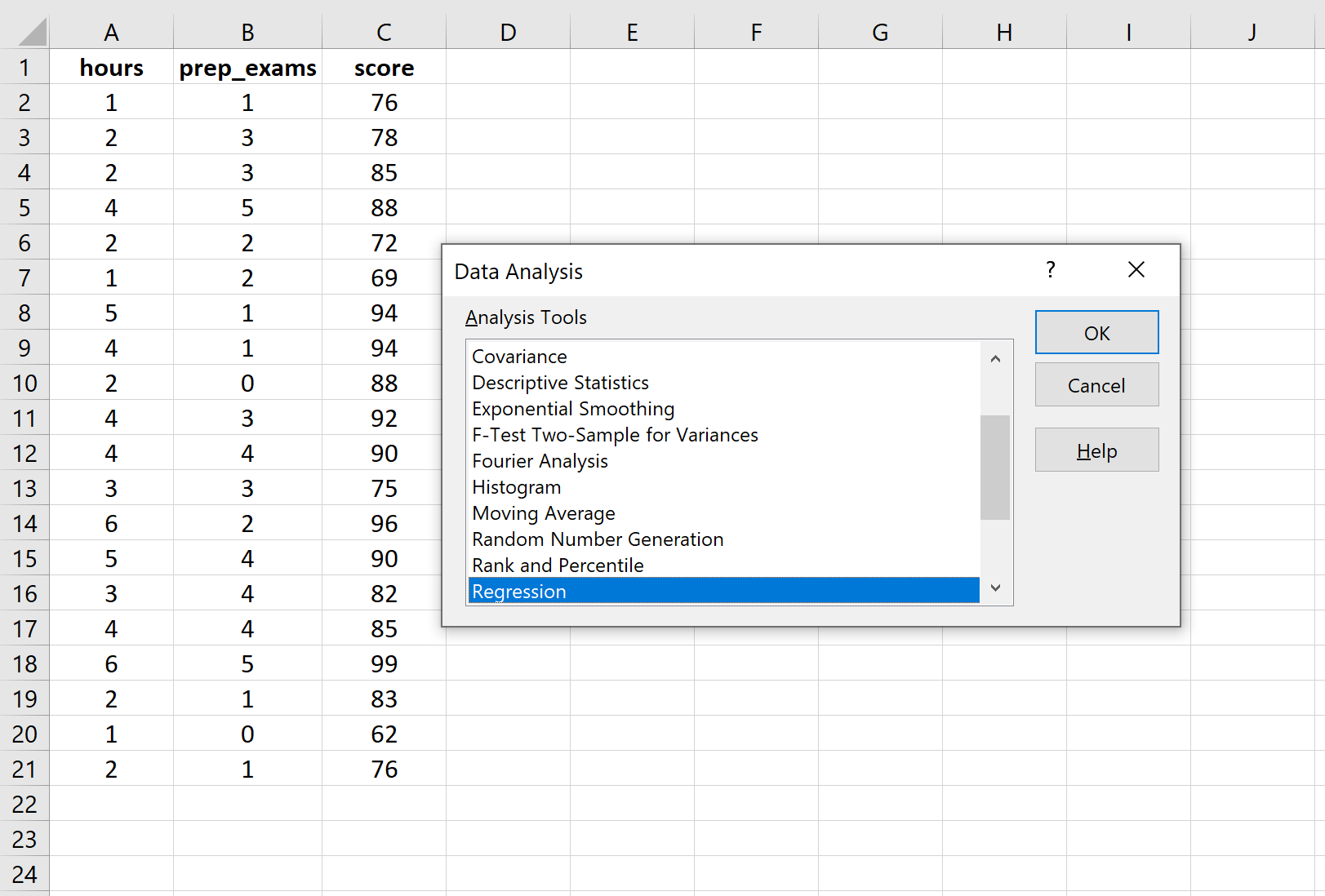
بالنسبة لنطاق الإدخال Y ، املأ مصفوفة القيم لمتغير الاستجابة. بالنسبة لنطاق الإدخال X ، املأ مصفوفة القيم للمتغيرين التوضيحيين. حدد المربع الموجود بجوار التسميات لإعلام Excel بأننا قمنا بتضمين أسماء المتغيرات في نطاقات الإدخال. بالنسبة لنطاق الإخراج ، حدد الخلية التي تريد ظهور مخرجات الانحدار فيها. ثم انقر فوق موافق .
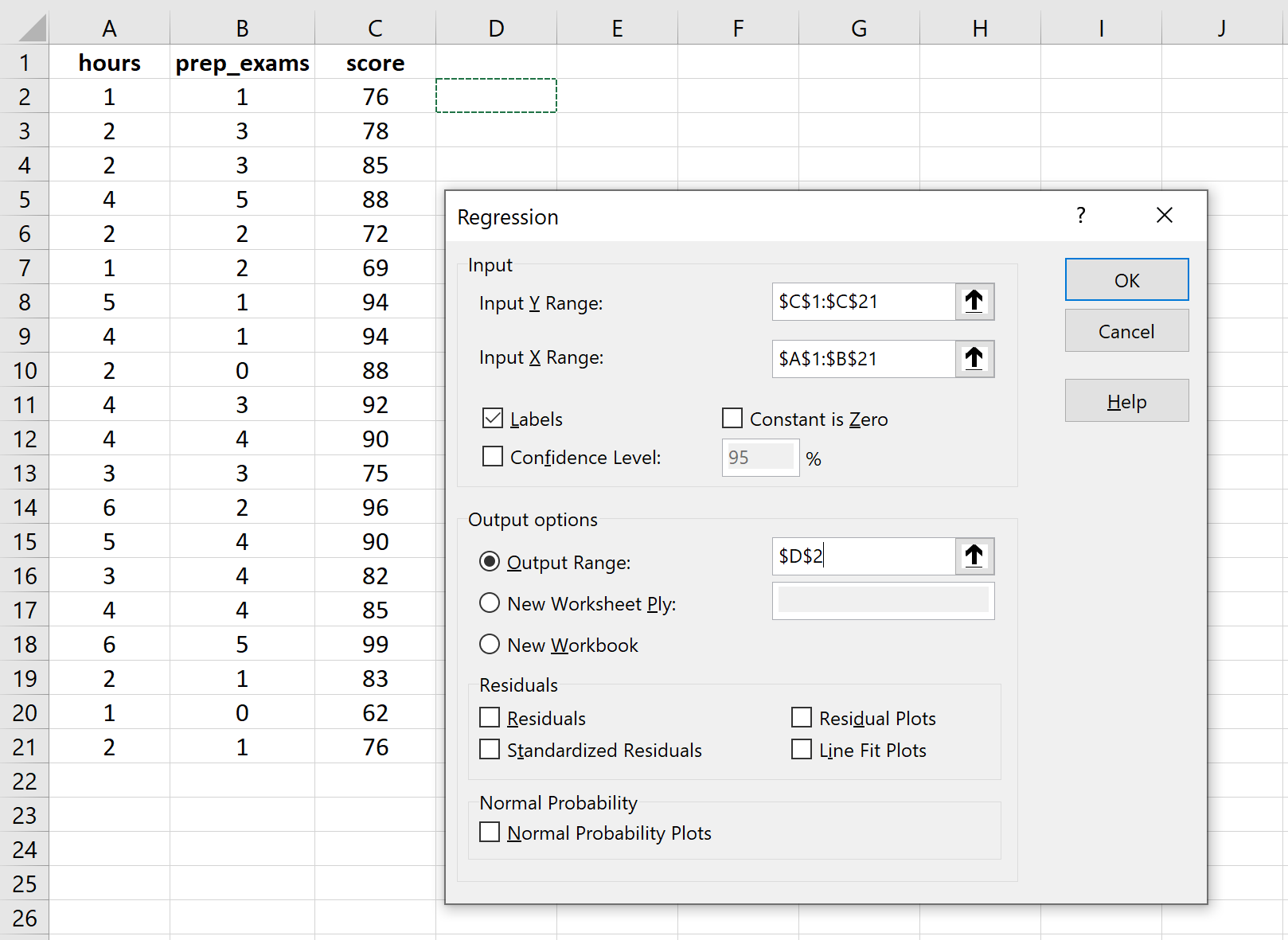
سيظهر الإخراج التالي تلقائيًا:
الخطوة 3: تفسير النتيجة.
فيما يلي كيفية تفسير الأرقام الأكثر صلة بالنتيجة:
ص مربع : 0.734 . وهذا ما يسمى معامل التحديد. هي نسبة تباين متغير الاستجابة التي يمكن تفسيرها بالمتغيرات التفسيرية. في هذا المثال، يتم تفسير 73.4% من التباين في درجات الامتحان بعدد ساعات الدراسة وعدد الاختبارات الإعدادية التي تم إجراؤها.
الخطأ المعياري : 5.366 . هذا هو متوسط المسافة بين القيم المرصودة وخط الانحدار. في هذا المثال، تنحرف القيم المرصودة في المتوسط بمقدار 5366 وحدة عن خط الانحدار.
F: 11:46 مساءً هذه هي إحصائية F الإجمالية لنموذج الانحدار، والتي يتم حسابها على أنها MS انحدار/MS المتبقية.
المعنى ف : 0.0000 . هذه هي القيمة p المرتبطة بإحصائيات F الإجمالية. يخبرنا هذا ما إذا كان نموذج الانحدار ككل ذو دلالة إحصائية أم لا. وبعبارة أخرى، فإنه يخبرنا ما إذا كان المتغيران التوضيحيان مجتمعان لهما ارتباط ذو دلالة إحصائية مع متغير الاستجابة. وفي هذه الحالة تكون القيمة p أقل من 0.05 مما يدل على أن المتغيرات التوضيحية وساعات الدراسة والاختبارات التحضيرية مجتمعة لها علاقة ذات دلالة إحصائية بنتيجة الامتحان .
القيم P. تخبرنا القيم p الفردية ما إذا كان كل متغير توضيحي ذو دلالة إحصائية أم لا. يمكننا أن نرى أن ساعات الدراسة ذات دلالة إحصائية (ع = 0.00) في حين أن الامتحانات التحضيرية التي تم إجراؤها (ع = 0.52) ليست ذات دلالة إحصائية عند α = 0.05. وبما أن الامتحانات الإعدادية السابقة ليست ذات دلالة إحصائية، فقد ينتهي بنا الأمر إلى اتخاذ قرار بإزالتها من النموذج.
المعاملات: تخبرنا معاملات كل متغير توضيحي بمتوسط التغير المتوقع في متغير الاستجابة، على افتراض بقاء المتغير التوضيحي الآخر ثابتا. على سبيل المثال، مقابل كل ساعة إضافية تقضيها في الدراسة، من المتوقع أن يزيد متوسط درجة الاختبار بمقدار 5.56 ، على افتراض أن الاختبارات التدريبية التي تم إجراؤها تظل ثابتة.
إليك طريقة أخرى للنظر إلى الأمر: إذا كان الطالب “أ” والطالب “ب” يأخذان نفس العدد من الاختبارات الإعدادية ولكن الطالب “أ” يدرس لمدة ساعة أطول، فيجب أن يسجل الطالب “أ” 5.56 نقطة أعلى من الطالب “ب”.
نفسر معامل الاعتراض على أنه يعني أن درجة الامتحان المتوقعة للطالب الذي لا يدرس ساعات ولا يقدم امتحانات تحضيرية هي 67.67 .
معادلة الانحدار المقدرة: يمكننا استخدام المعاملات من مخرجات النموذج لإنشاء معادلة الانحدار المقدرة التالية:
درجة الامتحان = 67.67 + 5.56*(ساعات) – 0.60*(الاختبارات التحضيرية)
يمكننا استخدام معادلة الانحدار المقدرة هذه لحساب درجة الاختبار المتوقعة للطالب، بناءً على عدد ساعات الدراسة وعدد الاختبارات التدريبية التي يقدمها. على سبيل المثال، الطالب الذي يدرس لمدة ثلاث ساعات ويتقدم لامتحان الإعدادية يجب أن يحصل على درجة 83.75 :
درجة الامتحان = 67.67 + 5.56*(3) – 0.60*(1) = 83.75
ضع في اعتبارك أنه نظرًا لأن الاختبارات الإعدادية السابقة لم تكن ذات دلالة إحصائية (p=0.52)، فقد نقرر إزالتها لأنها لا تقدم أي تحسين للنموذج العام. في هذه الحالة، يمكننا إجراء انحدار خطي بسيط باستخدام الساعات التي تمت دراستها فقط كمتغير توضيحي.
يمكن العثور على نتائج تحليل الانحدار الخطي البسيط هنا .
مصادر إضافية
بمجرد قيامك بإجراء الانحدار الخطي المتعدد، قد ترغب في التحقق من عدة افتراضات، بما في ذلك:
1. اختبار التعددية الخطية باستخدام VIF .
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر