الانحدار الخطي المتعدد يدويًا (خطوة بخطوة)
الانحدار الخطي المتعدد هو أسلوب يمكننا استخدامه لتحديد العلاقة بين متغيرين أو أكثر من متغيرات التوقع ومتغير الاستجابة .
يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار الخطي المتعدد يدويًا.
مثال: الانحدار الخطي المتعدد باليد
لنفترض أن لدينا مجموعة البيانات التالية مع متغير الاستجابة y ومتغيرين متوقعين x 1 و x 2 :
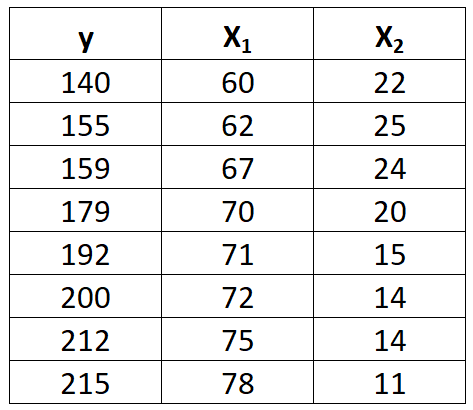
أكمل الخطوات التالية لتناسب نموذج الانحدار الخطي المتعدد لمجموعة البيانات هذه.
الخطوة 1: احسب x 1 2 , x 2 2 , x 1 y, x 2 y و x 1 x 2 .
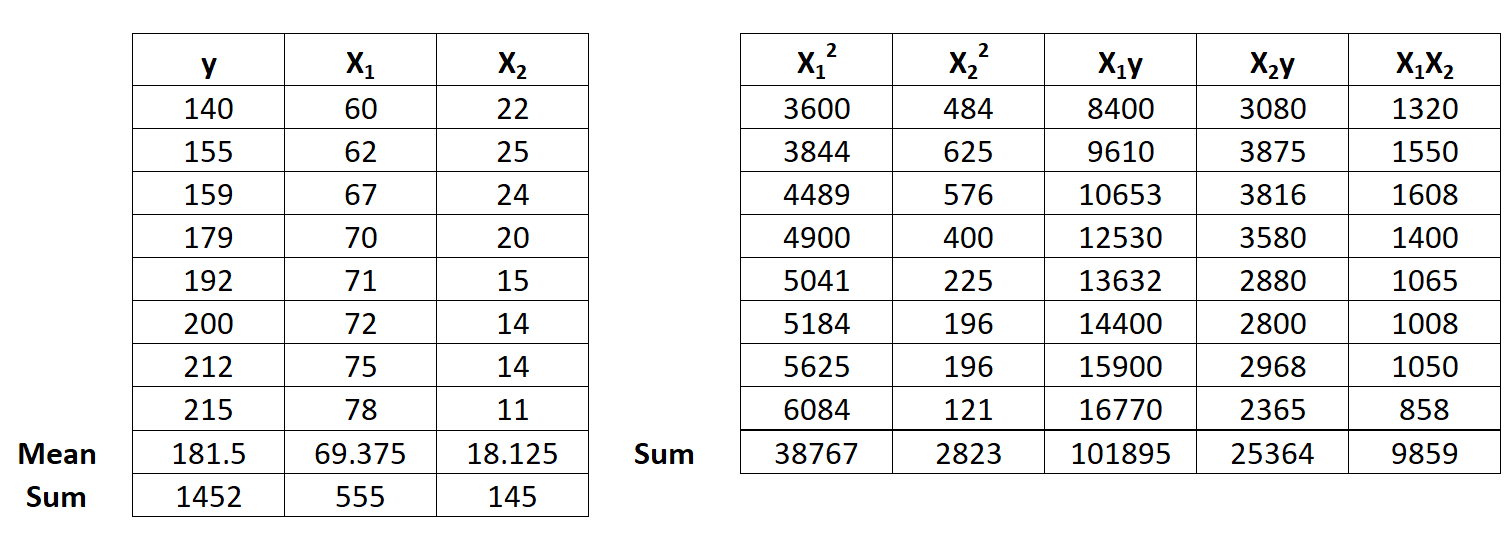
الخطوة 2: حساب مبالغ الانحدار.
بعد ذلك، قم بإجراء حسابات مجموع الانحدار التالية:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / ن = 38.767 – (555) 2 / 8 = 263.875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / ن = 2823 – (145) 2 / 8 = 194.875
- Σ × 1 ص = Σ
- Σ × 2 ص = Σ
- Σ × 1 × 2 = Σ
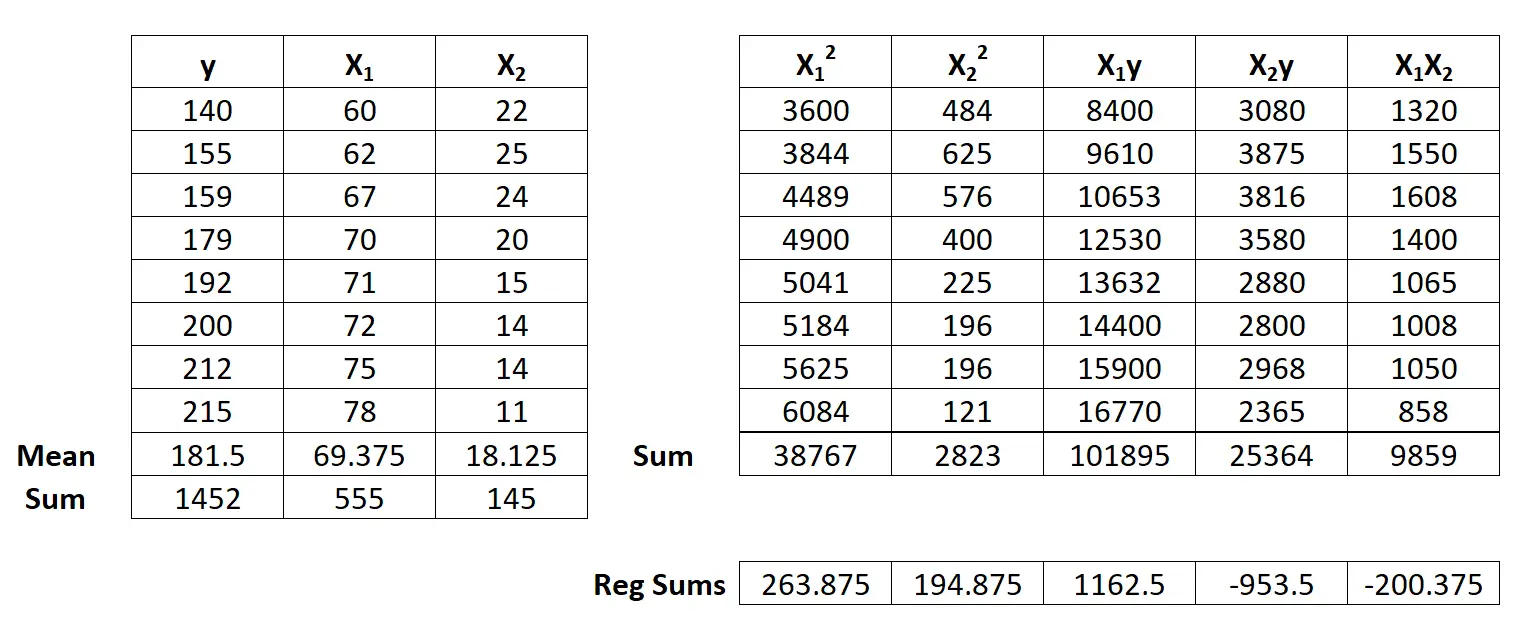
الخطوة 3: احسب ب 0 و ب 1 و ب 2 .
صيغة حساب b 1 هي: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) ) 2 ]
إذًا ب 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
صيغة حساب b 2 هي: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) ) 2 ]
إذن ب 2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375) 2 ] = -1.656
صيغة حساب b 0 هي: y – b 1 X 1 – b 2 X 2
وبالتالي، ب 0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
الخطوة 5: ضع b 0 و b 1 و b 2 في معادلة الانحدار الخطي المقدرة.
معادلة الانحدار الخطي المقدرة هي: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
في مثالنا، ŷ = -6.867 + 3.148x 1 – 1.656x 2
كيفية تفسير معادلة الانحدار الخطي المتعدد
فيما يلي كيفية تفسير معادلة الانحدار الخطي المقدرة: ŷ = -6.867 + 3.148x 1 – 1.656x 2
ب0 = -6.867 . عندما يكون كلا المتغيرين المتنبئين مساويين للصفر، فإن متوسط قيمة y هو -6.867.
ب1 = 3.148 . ترتبط زيادة وحدة واحدة في x 1 بزيادة قدرها 3.148 وحدة في y، في المتوسط، على افتراض أن x 2 يظل ثابتًا.
ب2 = -1.656 . ترتبط الزيادة بمقدار وحدة واحدة في x 2 بانخفاض قدره 1,656 وحدة في y، في المتوسط، على افتراض أن x 1 يظل ثابتًا.
مصادر إضافية
مقدمة للانحدار الخطي المتعدد
كيفية إجراء الانحدار الخطي البسيط باليد
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر