كيفية إجراء الانحدار الخطي المتعدد في sas

الانحدار الخطي المتعدد هو أسلوب يمكننا استخدامه لفهم العلاقة بين متغيرين أو أكثر من متغيرات التوقع ومتغير الاستجابة .

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار الخطي المتعدد في SAS.

الخطوة 1: إنشاء البيانات

لنفترض أننا نريد ملاءمة نموذج الانحدار الخطي المتعدد الذي يستخدم عدد الساعات التي يقضيها في الدراسة وعدد اختبارات التدريب التي تم إجراؤها للتنبؤ بدرجة الاختبار النهائي للطلاب:

درجة الامتحان = β ₀ + β ₁ (ساعات) + β ₂ (الاختبارات التحضيرية)

أولاً، سنستخدم الكود التالي لإنشاء مجموعة بيانات تحتوي على هذه المعلومات لـ 20 طالبًا:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

الخطوة 2: إجراء الانحدار الخطي المتعدد

بعد ذلك، سوف نستخدم proc reg لملاءمة نموذج الانحدار الخطي المتعدد مع البيانات:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

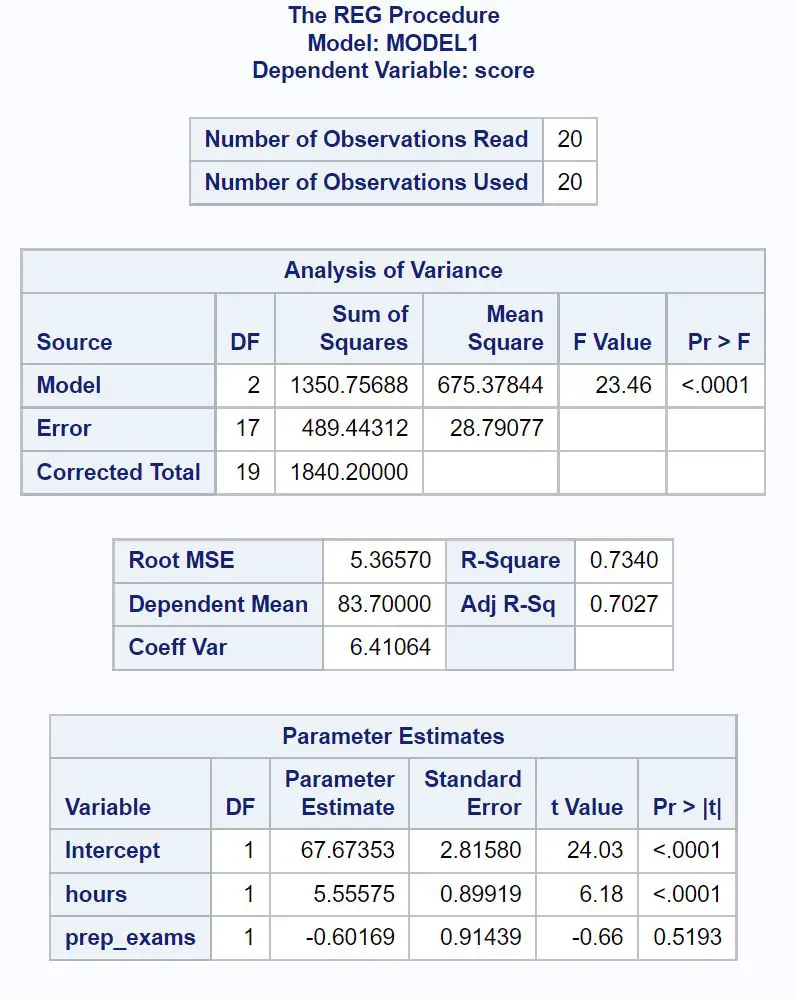
فيما يلي كيفية تفسير الأرقام الأكثر صلة في كل جدول:

جدول تحليل الفجوة:

القيمة F الإجمالية لنموذج الانحدار هي 23.46 والقيمة p المقابلة هي <0.0001 .

وبما أن هذه القيمة p أقل من 0.05، فإننا نستنتج أن نموذج الانحدار ككل له دلالة إحصائية.

الجدول المناسب للنموذج:

تخبرنا قيمة R-Square بنسبة التباين في درجات الامتحانات التي يمكن تفسيرها بعدد ساعات الدراسة وعدد الاختبارات الإعدادية التي تم إجراؤها.

بشكل عام، كلما زادت قيمة R-squared لنموذج الانحدار، كلما كانت متغيرات التوقع أفضل في التنبؤ بقيمة متغير الاستجابة.

وفي هذه الحالة يمكن تفسير 73.4% من التباين في درجات الامتحان بعدد الساعات المدروسة وعدد الاختبارات التحضيرية التي تم إجراؤها.

من المفيد أيضًا معرفة قيمة Root MSE . ويمثل هذا متوسط المسافة بين القيم المرصودة وخط الانحدار.

في نموذج الانحدار هذا، تنحرف القيم المرصودة في المتوسط بمقدار 5.3657 وحدة عن خط الانحدار.

جدول تقديرات المعلمة:

يمكننا استخدام قيم تقدير المعلمات في هذا الجدول لكتابة معادلة الانحدار المجهزة:

درجة الامتحان = 67.674 + 5.556*(ساعات) – 0.602*(امتحانات الإعدادية)

يمكننا استخدام هذه المعادلة للعثور على درجة الامتحان المقدرة للطالب، بناءً على عدد ساعات الدراسة وعدد الاختبارات التدريبية التي أجراها.

على سبيل المثال، الطالب الذي يدرس لمدة 3 ساعات ويتقدم لامتحانين تحضيريين يجب أن يحصل على درجة 83.1 في الامتحان:

درجة الاختبار المقدرة = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

القيمة p للساعات (<0.0001) أقل من 0.05، مما يعني أن لها علاقة ذات دلالة إحصائية بنتيجة الامتحان.

إلا أن قيمة p للامتحانات الإعدادية (0.5193) لا تقل عن 0.05، مما يعني أنه لا يوجد ارتباط ذو دلالة إحصائية بنتيجة الامتحان.

قد نقرر إزالة الاختبارات التحضيرية من النموذج، لأنها ليست ذات دلالة إحصائية، وبدلاً من ذلك نقوم بإجراء انحدار خطي بسيط باستخدام ساعات الدراسة كمتغير متنبئ وحيد.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في SAS:

كيفية حساب الارتباط في SAS
كيفية إجراء الانحدار الخطي البسيط في SAS
كيفية إجراء ANOVA أحادي الاتجاه في SAS