كيفية إجراء الانحدار اللوجستي في spss

الانحدار اللوجستي هو أسلوب نستخدمه لملاءمة نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار اللوجستي في SPSS.

مثال: الانحدار اللوجستي في SPSS

استخدم الخطوات التالية لإجراء الانحدار اللوجستي في SPSS لمجموعة بيانات تشير إلى ما إذا كان لاعبو كرة السلة الجامعيون قد تم تجنيدهم في الدوري الاميركي للمحترفين أم لا (مسودة: 0 = لا، 1 = نعم) بناءً على المعدل التراكمي الخاص بهم. النقاط لكل مباراة ومستوى تقسيمها.

الخطوة 1: أدخل البيانات.

أولا قم بإدخال البيانات التالية:

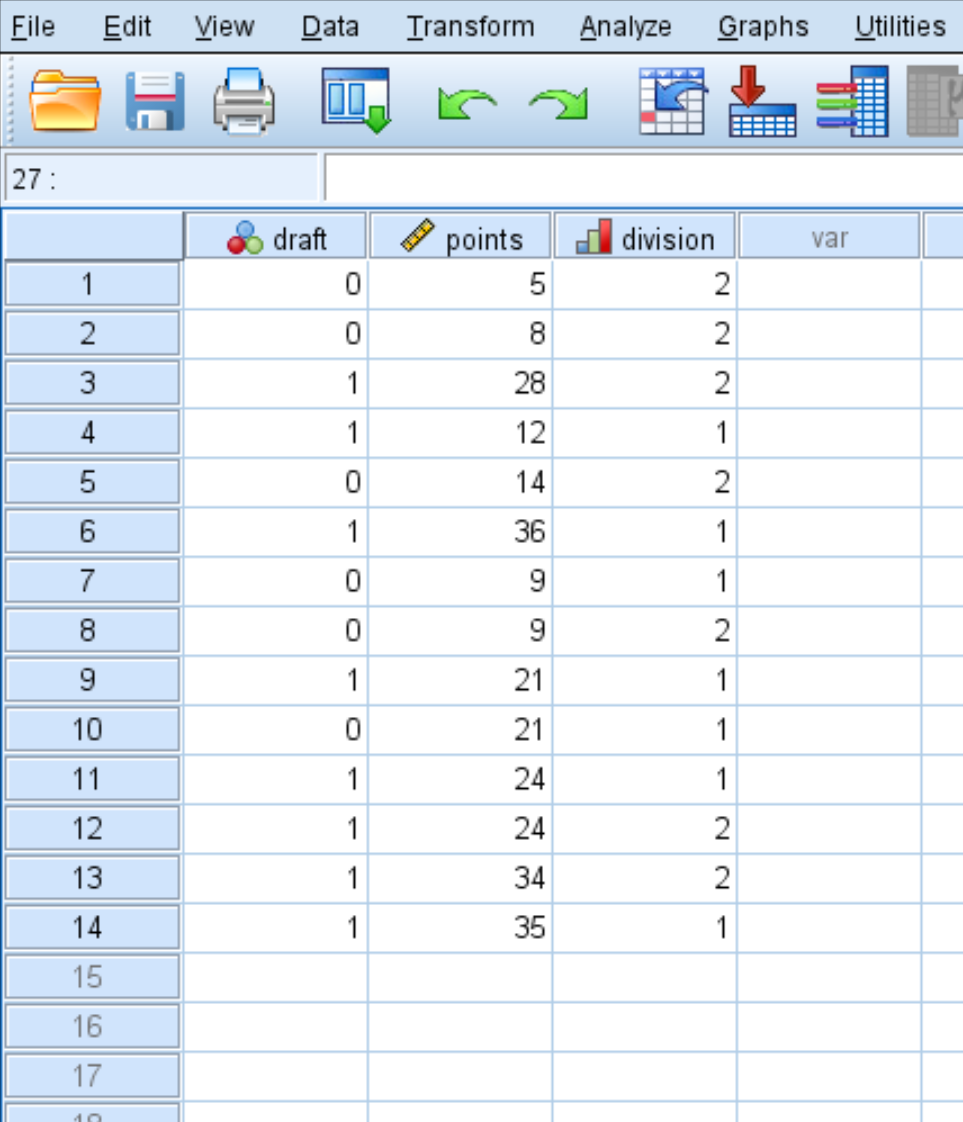
الخطوة 2: تنفيذ الانحدار اللوجستي.

انقر فوق علامة التبويب تحليل ، ثم الانحدار ، ثم الانحدار اللوجستي الثنائي :

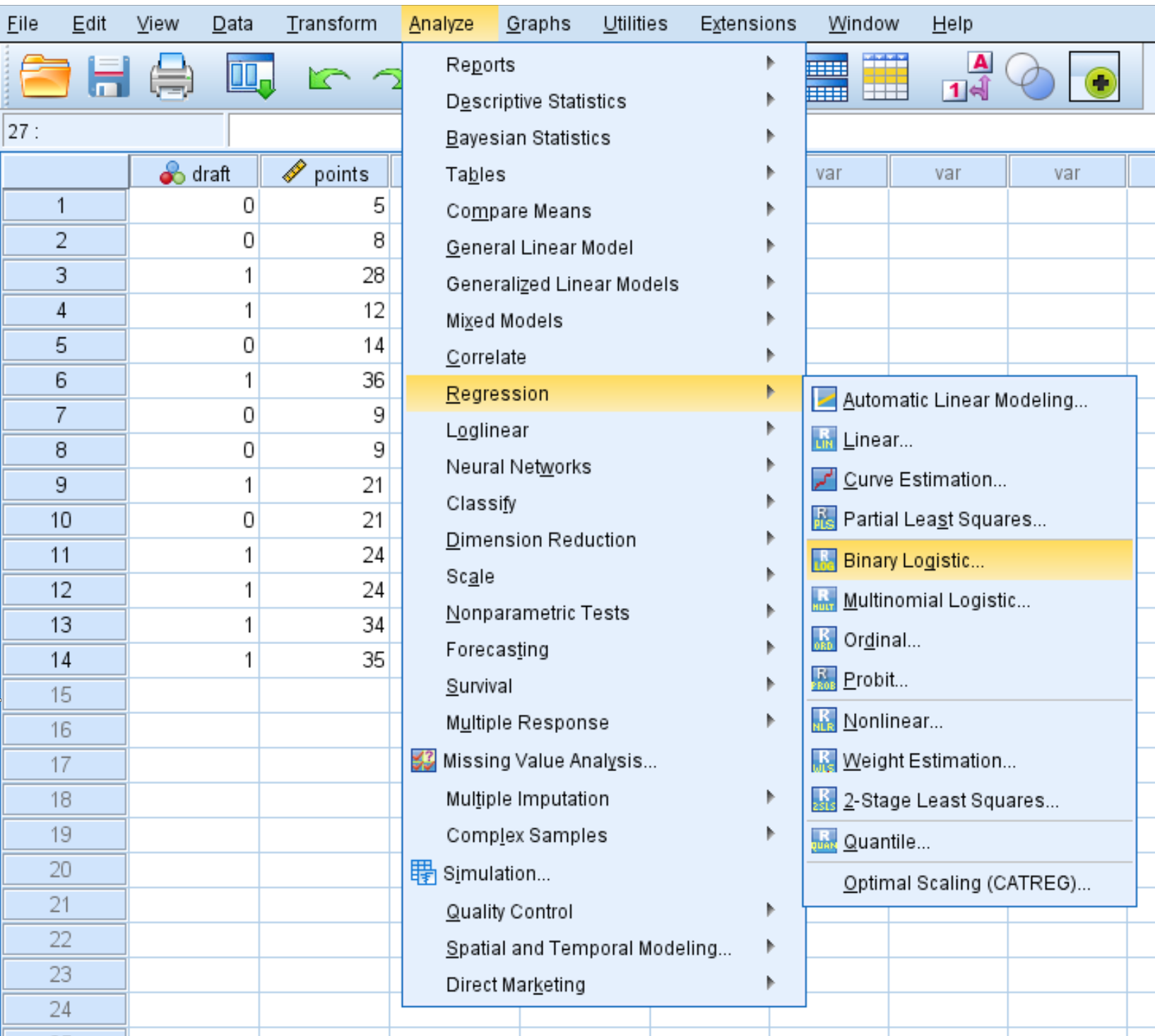
في النافذة الجديدة التي تظهر، اسحب مشروع متغير الاستجابة الثنائية إلى المنطقة المسماة “تابع”. ثم اسحب النقطتين وتقسيم متغيرات التوقع إلى المربع المسمى الكتلة 1 من 1. اترك الطريقة مضبوطة على Enter. ثم انقر فوق موافق .

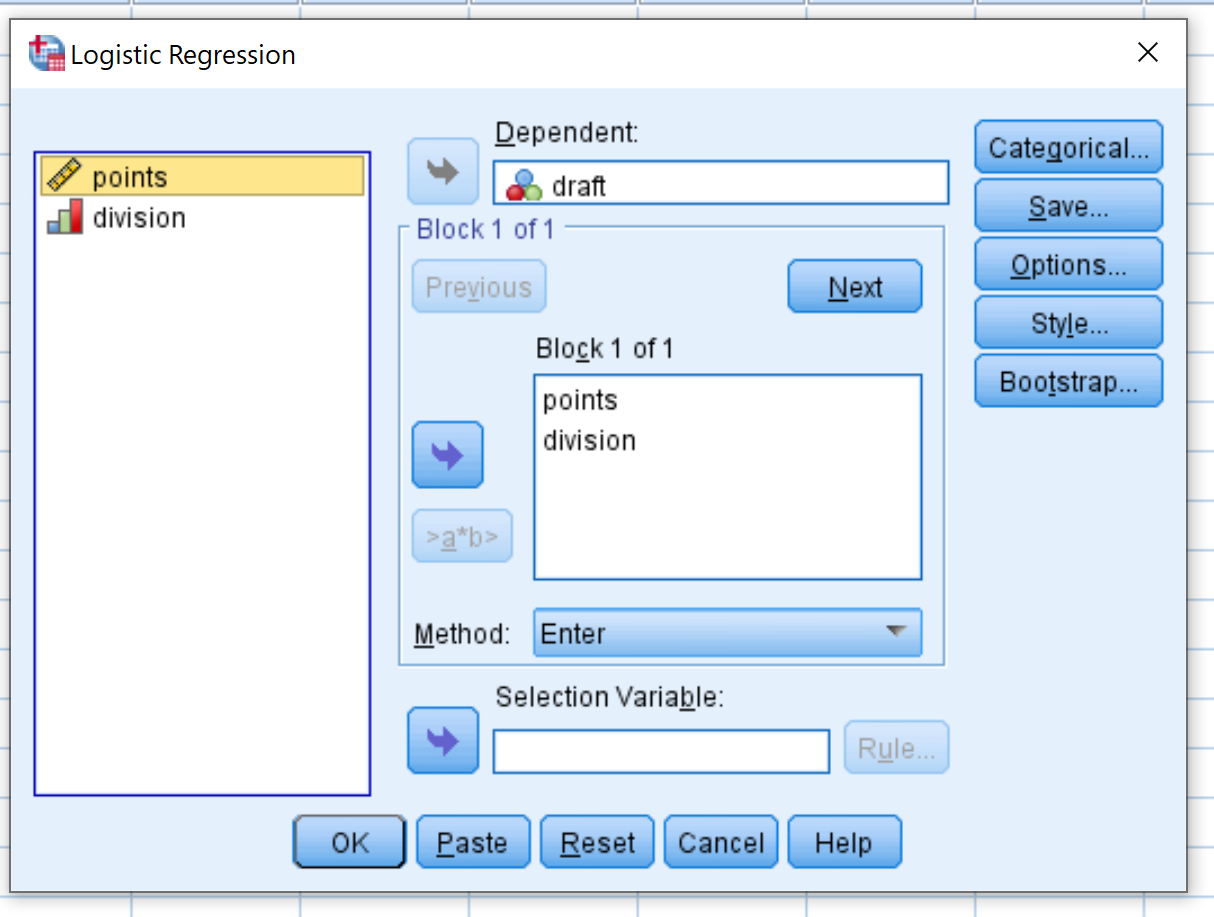
الخطوة 3. تفسير النتيجة.

بمجرد النقر فوق “موافق” ، ستظهر نتيجة الانحدار اللوجستي:

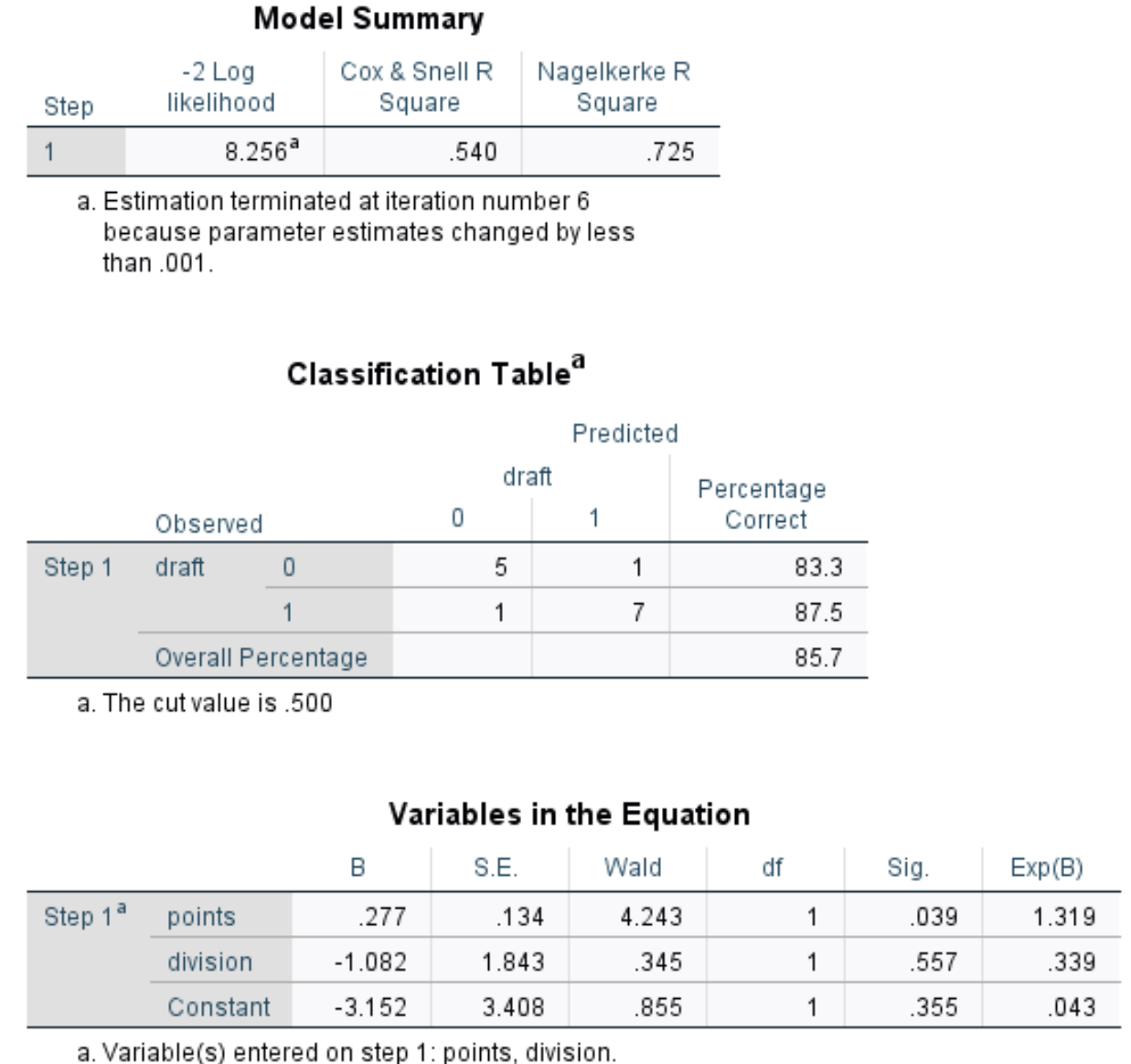
وإليك كيفية تفسير النتيجة:

ملخص النموذج: المقياس الأكثر فائدة في هذا الجدول هو Nagelkerke R Square، والذي يخبرنا بنسبة التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة المتغيرات المتوقعة. في هذه الحالة، النقاط والقسمة يمكن أن تفسر 72.5% من تباين المسودة.

جدول التصنيف: المقياس الأكثر فائدة في هذا الجدول هو النسبة المئوية الإجمالية، والتي تخبرنا النسبة المئوية للملاحظات التي تمكن النموذج من تصنيفها بشكل صحيح. في هذه الحالة، كان نموذج الانحدار اللوجستي قادرًا على التنبؤ بشكل صحيح بنتيجة المسودة لـ 85.7% من اللاعبين.

متغيرات المعادلة: يقدم لنا هذا الجدول الأخير عدة قياسات مفيدة منها:

• والد: إحصائية اختبار والد لكل متغير متنبئ، والتي تستخدم لتحديد ما إذا كان كل متغير متنبئ ذو دلالة إحصائية أم لا.
• Sig: القيمة p التي تتوافق مع إحصائيات اختبار Wald لكل متغير متنبئ. نرى أن القيمة الاحتمالية للنقاط هي 0.039 والقيمة الاحتمالية للقسمة هي 0.557.
• Exp(B): نسبة الأرجحية لكل متغير متنبئ. يخبرنا هذا بالتغير في احتمالات تجنيد اللاعب المرتبط بزيادة وحدة واحدة في متغير توقع معين. على سبيل المثال، احتمالات تجنيد لاعب من الدرجة الثانية هي 0.339 فقط من احتمالات تجنيد لاعب من الدرجة الأولى. وبالمثل، ترتبط كل وحدة إضافية زيادة في النقاط لكل لعبة بزيادة قدرها 1319 في احتمالات تجنيد اللاعب.

يمكننا بعد ذلك استخدام المعاملات (القيم الموجودة في العمود المسمى B) للتنبؤ باحتمالية استدعاء لاعب معين، باستخدام الصيغة التالية:

الاحتمال = ه ^{-3.152 + 0.277 (نقاط) – 1.082 (قسمة)} / (1+ه ^{-3.152 + 0.277 (نقاط) – 1.082 (قسمة)} )

على سبيل المثال، يمكن حساب احتمالية انضمام اللاعب الذي يبلغ متوسطه 20 نقطة لكل مباراة ويلعب في القسم 1 على النحو التالي:

الاحتمال = e ^{-3.152 + 0.277(20) – 1.082(1)} / (1+e ^{-3.152 + 0.277(20) – 1.082(1)} ) = 0.787 .

وبما أن هذا الاحتمال أكبر من 0.5، فإننا نتوقع أن يتم تجنيد هذا اللاعب.

الخطوة 4. الإبلاغ عن النتائج.

وأخيرا، نود أن نورد نتائج الانحدار اللوجستي لدينا. فيما يلي مثال لكيفية القيام بذلك:

تم إجراء الانحدار اللوجستي لتحديد كيفية تأثير النقاط لكل لعبة ومستوى القسم على احتمالية تجنيد لاعب كرة السلة. تم استخدام ما مجموعه 14 لاعبا في التحليل.

وأوضح النموذج 72.5% من التباين في نتائج المشروع وصنف بشكل صحيح 85.7% من الحالات.

كانت احتمالات تجنيد لاعب من الدرجة الثانية 0.339 فقط من احتمالات تجنيد لاعب من الدرجة الأولى.

ارتبطت كل وحدة إضافية زيادة في النقاط لكل لعبة بزيادة قدرها 1319 في احتمالات تجنيد اللاعب.