كيفية إجراء الانحدار اللوجستي في sas

الانحدار اللوجستي هو طريقة يمكننا استخدامها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا.

يستخدم الانحدار اللوجستي طريقة تعرف بتقدير الاحتمالية القصوى للعثور على معادلة بالشكل التالي:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

ذهب:

• X _j : ^{المتغير} التنبئي j
• β _j : تقدير معامل المتغير التنبئي ^j

تتنبأ الصيغة الموجودة على الجانب الأيمن من المعادلة باحتمالات السجل التي يأخذ فيها متغير الاستجابة القيمة 1.

يوضح المثال التالي خطوة بخطوة كيفية ملاءمة نموذج الانحدار اللوجستي في SAS.

الخطوة 1: إنشاء مجموعة البيانات

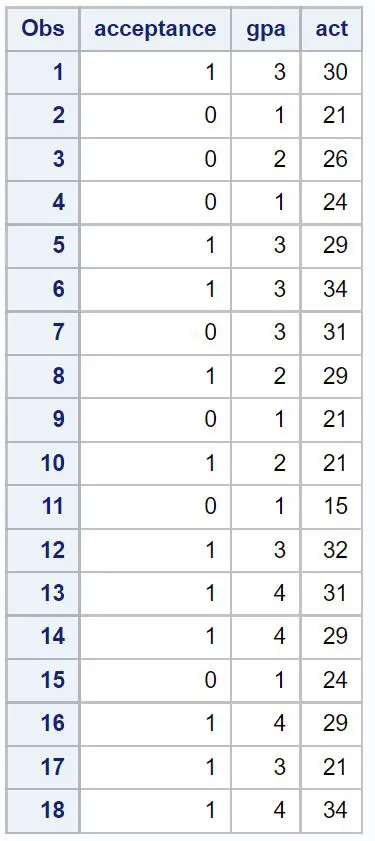
أولاً، سنقوم بإنشاء مجموعة بيانات تحتوي على معلومات حول المتغيرات الثلاثة التالية لـ 18 طالبًا:

• القبول في كلية معينة (1 = نعم، 0 = لا)
• المعدل التراكمي (مقياس من 1 إلى 4)
• درجة ACT (مقياس من 1 إلى 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

الخطوة 2: ملاءمة نموذج الانحدار اللوجستي

بعد ذلك، سوف نستخدم لوجستيات proc لتناسب نموذج الانحدار اللوجستي، باستخدام “القبول” كمتغير الاستجابة و”gpa” و”act” كمتغيرات متوقعة.

ملاحظة : يجب تحديد التناقص لـ SAS للتنبؤ باحتمال أن يأخذ متغير الاستجابة قيمة 1. افتراضيًا، يتنبأ SAS باحتمال أن يأخذ متغير الاستجابة قيمة 0.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

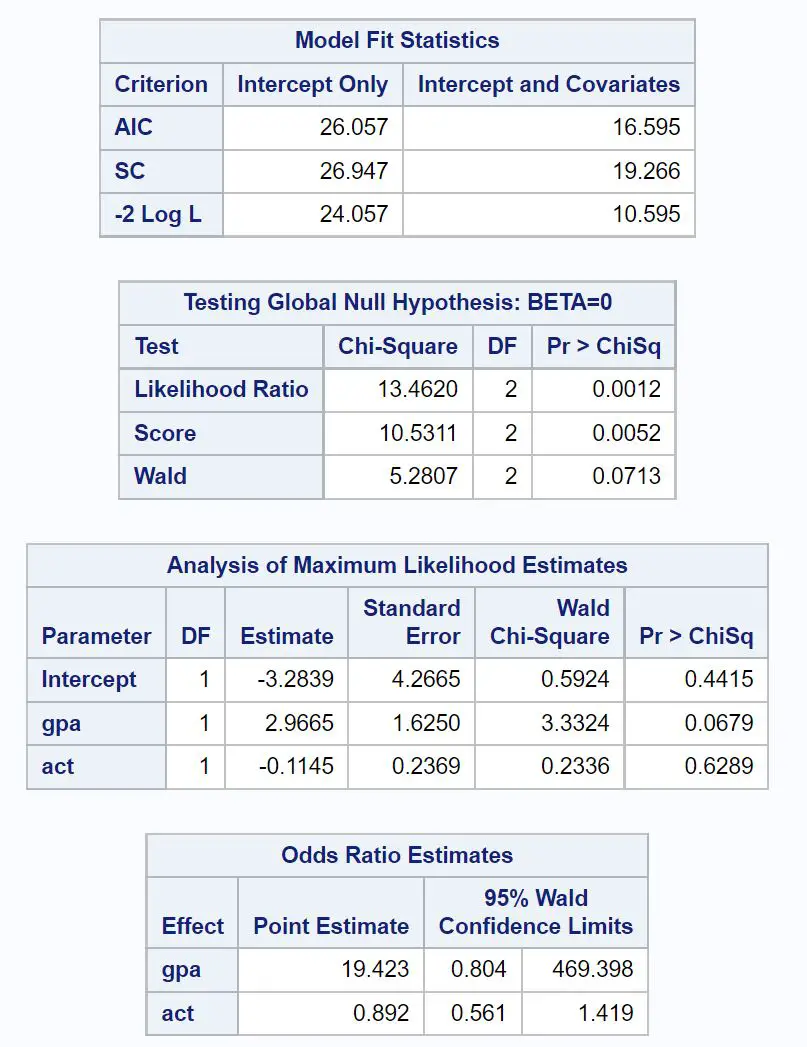
الجدول الأول محل الاهتمام يحمل عنوان Model Fit Statistics .

من هذا الجدول يمكننا أن نرى قيمة AIC للنموذج، والتي تبين أنها 16.595 . كلما انخفضت قيمة AIC، كانت قدرة النموذج على ملاءمة البيانات أفضل.

ومع ذلك، لا يوجد حد لما يعتبر قيمة AIC “جيدة” . بدلاً من ذلك، نستخدم AIC لمقارنة مدى ملاءمة نماذج متعددة لنفس مجموعة البيانات. يعتبر النموذج ذو أدنى قيمة AIC هو الأفضل بشكل عام.

يحمل الجدول التالي محل الاهتمام اختبار الفرضية الصفرية العالمية: BETA=0 .

من هذا الجدول، يمكننا أن نرى قيمة نسبة احتمالية لمربع كاي تبلغ 13.4620 مع القيمة الاحتمالية المقابلة البالغة 0.0012 .

وبما أن هذه القيمة p أقل من 0.05، فإن هذا يخبرنا أن نموذج الانحدار اللوجستي ككل له دلالة إحصائية.

بعد ذلك، يمكننا تحليل تقديرات المعامل في الجدول المعنون تحليل تقديرات الاحتمالية القصوى .

من هذا الجدول يمكننا أن نرى معاملات المعدل التراكمي والتصرف، والتي تشير إلى متوسط التغير في سجل احتمالات القبول في الكلية بزيادة وحدة واحدة في كل متغير.

على سبيل المثال:

• ترتبط زيادة وحدة واحدة في قيمة المعدل التراكمي بمتوسط زيادة قدرها 2.9665 في سجل احتمالات القبول في الكلية.
• ترتبط زيادة وحدة واحدة في درجة ACT بمتوسط انخفاض قدره 0.1145 في احتمالات القبول في الكلية.

تعطينا القيم p المقابلة في النتيجة أيضًا فكرة عن مدى فعالية كل متغير متنبئ في التنبؤ باحتمالية قبوله:

• القيمة P للمعدل التراكمي: 0.0679
• قيمة ACT P: 0.6289

يخبرنا هذا أن المعدل التراكمي يبدو مؤشرا ذا دلالة إحصائية للقبول في الكلية، في حين أن درجة ACT لا تبدو ذات دلالة إحصائية.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية ملاءمة نماذج الانحدار الأخرى في SAS:

كيفية إجراء الانحدار الخطي البسيط في SAS
كيفية إجراء الانحدار الخطي المتعدد في SAS