الانحدار اللوغاريتمي في r (خطوة بخطوة)

الانحدار اللوغاريتمي هو نوع من الانحدار يستخدم لنمذجة المواقف التي يتسارع فيها النمو أو الانخفاض بسرعة في البداية ثم يتباطأ بمرور الوقت.

على سبيل المثال، يوضح الرسم البياني التالي مثالاً على الاضمحلال اللوغاريتمي:

بالنسبة لهذا النوع من المواقف، يمكن صياغة العلاقة بين متغير التوقع ومتغير الاستجابة بشكل جيد باستخدام الانحدار اللوغاريتمي.

تأخذ معادلة نموذج الانحدار اللوغاريتمي الشكل التالي:

ص = أ + ب*لن(خ)

ذهب:

• y: متغير الاستجابة
• x: المتغير التنبؤي
• a,b: معاملات الانحدار التي تصف العلاقة بين x و y

يوضح المثال التالي خطوة بخطوة كيفية إجراء الانحدار اللوغاريتمي في R.

الخطوة 1: إنشاء البيانات

أولاً، لنقم بإنشاء بيانات وهمية لمتغيرين: x و y :

 x=1:15

y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)

الخطوة 2: تصور البيانات

بعد ذلك، لنقم بإنشاء مخطط تشتت سريع لتصور العلاقة بين x و y :

 plot(x, y) 

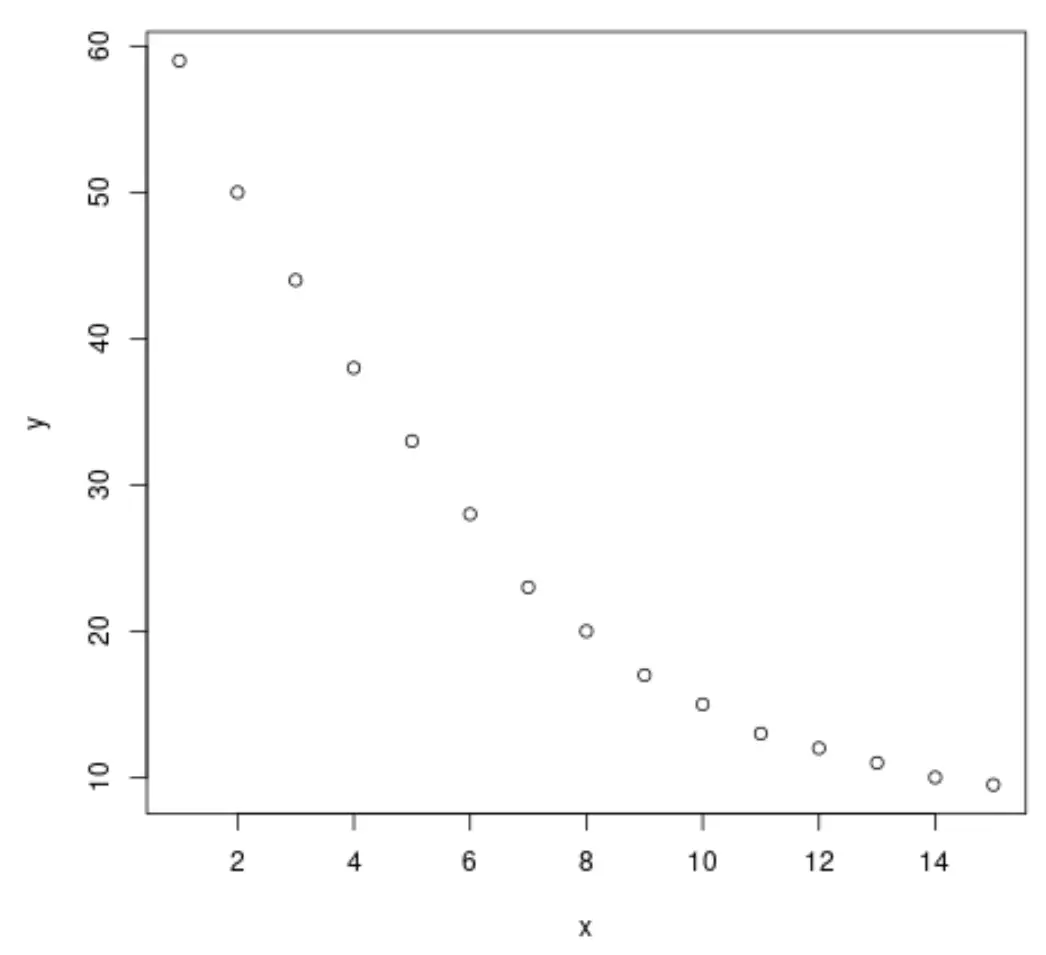
من الرسم البياني، يمكننا أن نرى أن هناك نمط اضمحلال لوغاريتمي واضح بين المتغيرين. قيمة متغير الاستجابة y تتناقص بسرعة في البداية، ثم تتباطأ مع مرور الوقت.

ولذلك يبدو من الحكمة ملاءمة معادلة الانحدار اللوغاريتمي لوصف العلاقة بين المتغيرات.

الخطوة 3: ملاءمة نموذج الانحدار اللوغاريتمي

بعد ذلك، سوف نستخدم الدالة lm() لتناسب نموذج الانحدار اللوغاريتمي، باستخدام اللوغاريتم الطبيعي لـ x كمتغير متوقع و y كمتغير الاستجابة.

 #fit the model
model <- lm(y ~ log (x))

#view the output of the model
summary(model)

Call:
lm(formula = y ~ log(x))

Residuals:
   Min 1Q Median 3Q Max 
-4.069 -1.313 -0.260 1.127 3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.0686 1.4090 44.76 1.25e-15 ***
log(x) -20.1987 0.7019 -28.78 3.70e-13 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.054 on 13 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 
F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13

القيمة F الإجمالية للنموذج هي 828.2 والقيمة p المقابلة منخفضة للغاية (3.702e-13)، مما يشير إلى أن النموذج ككل مفيد.

باستخدام المعاملات من جدول الإخراج، يمكننا أن نرى أن معادلة الانحدار اللوغاريتمي المجهزة هي:

ص = 63.0686 – 20.1987 * قانون الجنسية(س)

يمكننا استخدام هذه المعادلة للتنبؤ بمتغير الاستجابة y بناءً على قيمة المتغير المتنبئ x . على سبيل المثال، إذا كانت x = 12، فسنتوقع أن y ستكون 12.87 :

ص = 63.0686 – 20.1987 * قانون الجنسية (12) = 12.87

المكافأة: لا تتردد في استخدام حاسبة الانحدار اللوغاريتمي عبر الإنترنت لحساب معادلة الانحدار اللوغاريتمي تلقائيًا لمتنبئ معين ومتغير استجابة.

الخطوة 4: تصور نموذج الانحدار اللوغاريتمي

أخيرًا، يمكننا إنشاء رسم بياني سريع لتصور مدى ملاءمة نموذج الانحدار اللوغاريتمي للبيانات:

 #plot x vs. y
plot(x, y)

#define x-values to use for regression line
x=seq(from= 1 , to= 15 , length. out = 1000 )

#use the model to predict the y-values based on the x-values
y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )),
          interval=" confidence ")

#add the fitted regression line to the plot (lwd specifies the width of the line)
matlines(x,y, lwd= 2 )

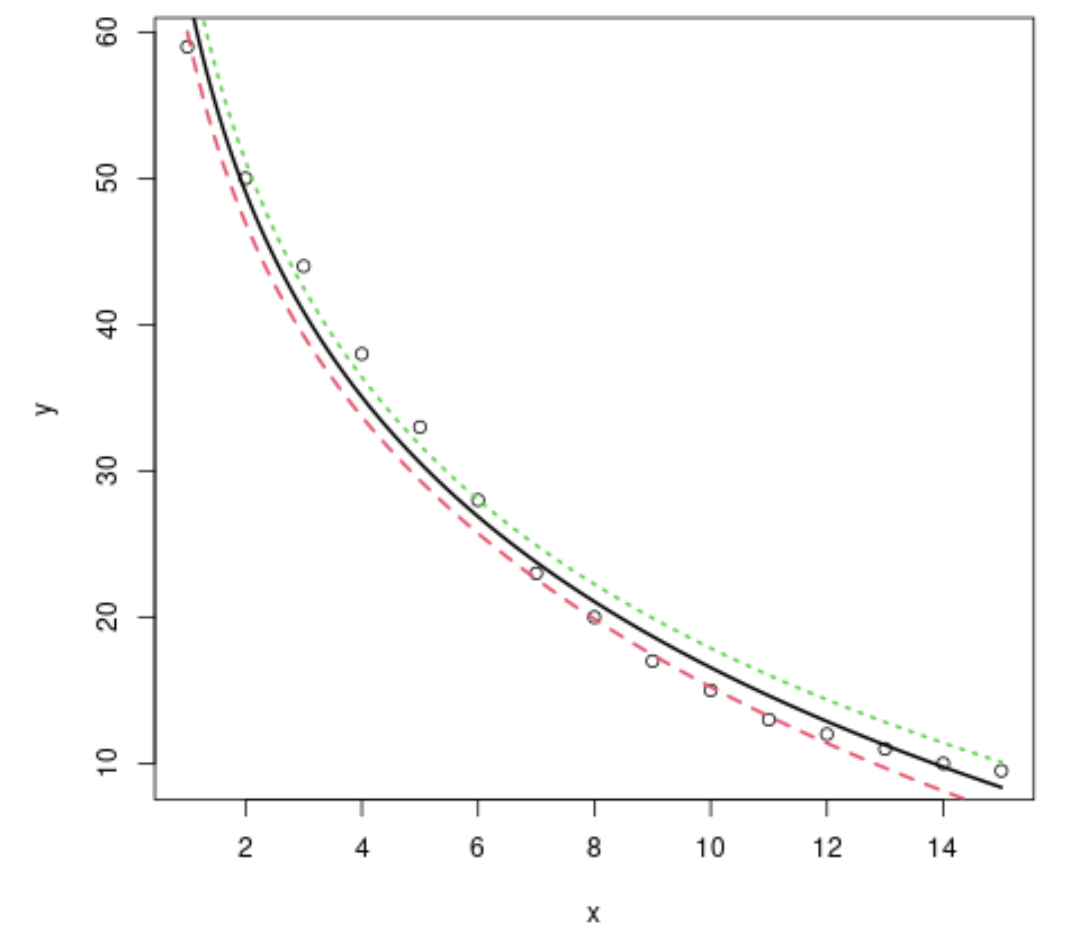
يمكننا أن نرى أن نموذج الانحدار اللوغاريتمي يقوم بعمل جيد في ملاءمة مجموعة البيانات هذه.

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إجراء الانحدار التربيعي في R
كيفية إجراء الانحدار الأسي في R
كيفية إجراء الانحدار متعدد الحدود في R