كيفية تنفيذ الانحدار المكعب في بايثون

الانحدار المكعب هو نوع من الانحدار الذي يمكننا استخدامه لتحديد العلاقة بين متغير التوقع ومتغير الاستجابة عندما تكون العلاقة بين المتغيرات غير خطية.

يشرح هذا البرنامج التعليمي كيفية إجراء الانحدار التكعيبي في بايثون.

مثال: الانحدار المكعب في بايثون

لنفترض أن لدينا DataFrame الباندا التالية التي تحتوي على متغيرين (x و y):

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

إذا قمنا بعمل مخطط تشتت بسيط لهذه البيانات، يمكننا أن نرى أن العلاقة بين المتغيرين غير خطية:

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

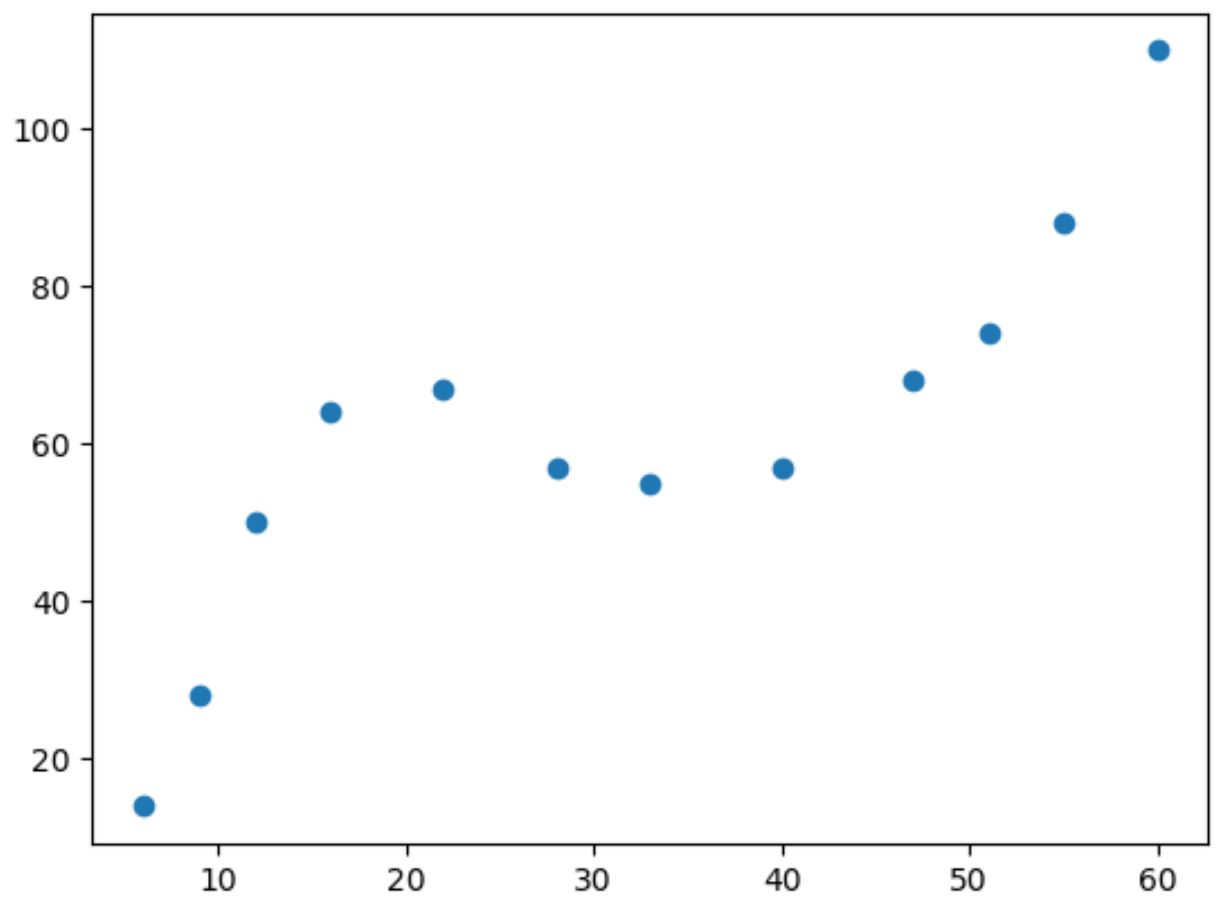
كلما زادت قيمة x، تزداد y إلى نقطة معينة، ثم تنخفض، ثم تزيد مرة أخرى.

هذا النمط ذو “منحنيين” في المخطط هو إشارة إلى وجود علاقة مكعبة بين المتغيرين.

وهذا يعني أن نموذج الانحدار المكعب هو مرشح جيد لقياس العلاقة بين المتغيرين.

لإجراء الانحدار التكعيبي، يمكننا ملاءمة نموذج الانحدار متعدد الحدود مع الدرجة 3 باستخدام الدالة numpy.polyfit() :

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

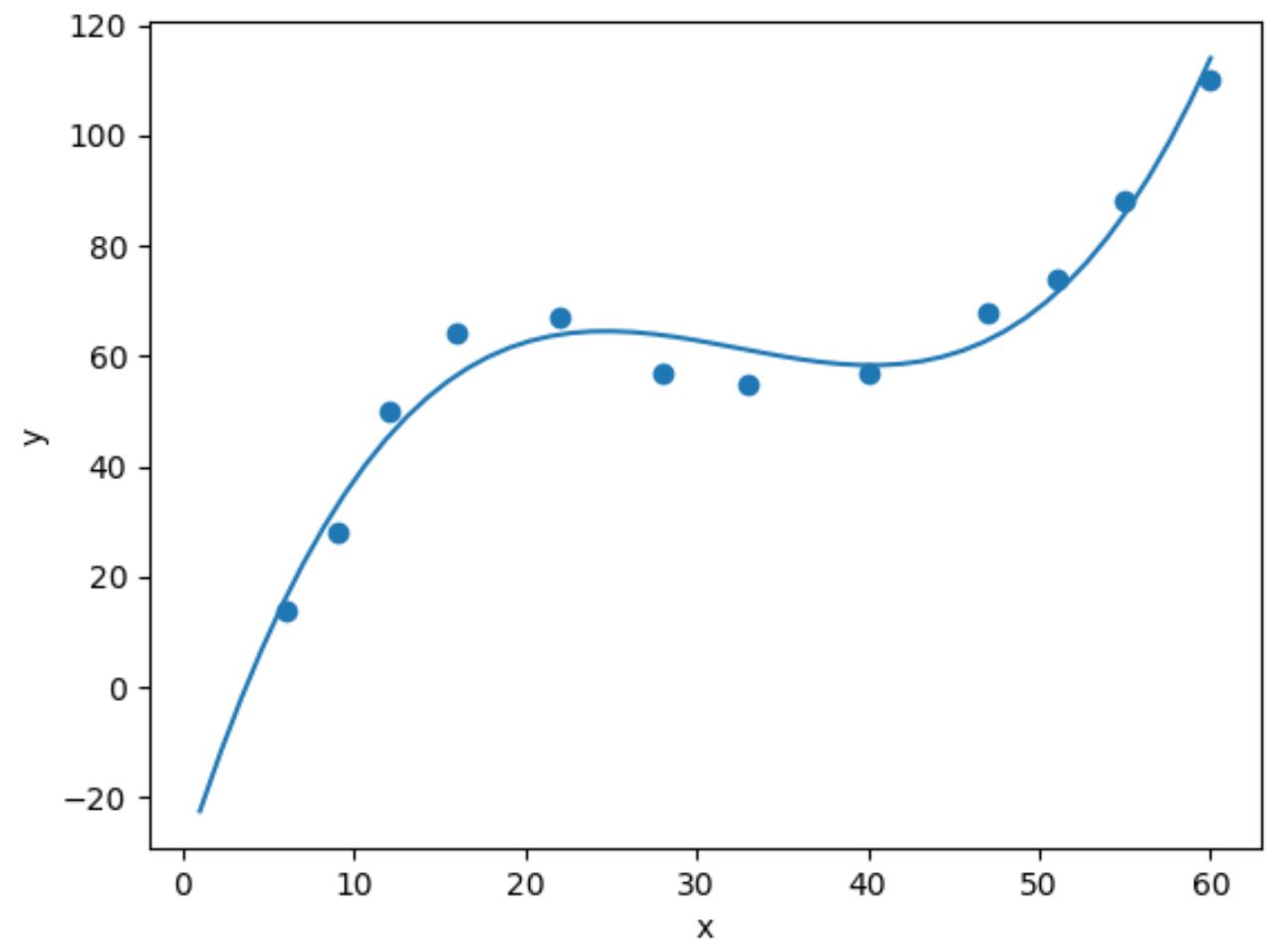
يمكننا الحصول على معادلة الانحدار التكعيبي المجهزة من خلال طباعة معاملات النموذج:

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

معادلة الانحدار المكعب المجهزة هي:

ص = 0.003302(س) ³ – 0.3214(س) ² + 9.832س – 30.01

يمكننا استخدام هذه المعادلة لحساب القيمة المتوقعة لـ y بناءً على قيمة x.

على سبيل المثال، إذا كانت x تساوي 30، فإن القيمة المتوقعة لـ y هي 64.844:

ص = 0.003302(30) ³ – 0.3214(30) ² + 9.832(30) – 30.01 = 64.844

يمكننا أيضًا كتابة دالة قصيرة للحصول على مربع R للنموذج، وهي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغيرات المتوقعة.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

في هذا المثال، مربع R للنموذج هو 0.9632 .

وهذا يعني أن 96.32% من التباين في متغير الاستجابة يمكن تفسيره بواسطة المتغير المتنبئ.

وبما أن هذه القيمة عالية جدًا، فإنها تخبرنا أن نموذج الانحدار المكعب يحدد العلاقة بين المتغيرين بشكل جيد.

ذات صلة: ما هي قيمة R-squared الجيدة؟

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في بايثون:

كيفية إجراء الانحدار الخطي البسيط في بايثون
كيفية إجراء الانحدار التربيعي في بايثون
كيفية إجراء الانحدار متعدد الحدود في بايثون