كيفية إجراء الانحدار متعدد الحدود باستخدام scikit-learn

الانحدار متعدد الحدود هو أسلوب يمكننا استخدامه عندما تكون العلاقة بين متغير التوقع ومتغير الاستجابة غير خطية.

يأخذ هذا النوع من الانحدار الشكل:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

حيث h هي “درجة” كثيرة الحدود.

يوضح المثال التالي خطوة بخطوة كيفية تنفيذ الانحدار متعدد الحدود في بايثون باستخدام sklearn.

الخطوة 1: إنشاء البيانات

أولاً، لنقم بإنشاء مصفوفتين NumPy للاحتفاظ بقيم المتنبئ ومتغير الاستجابة:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

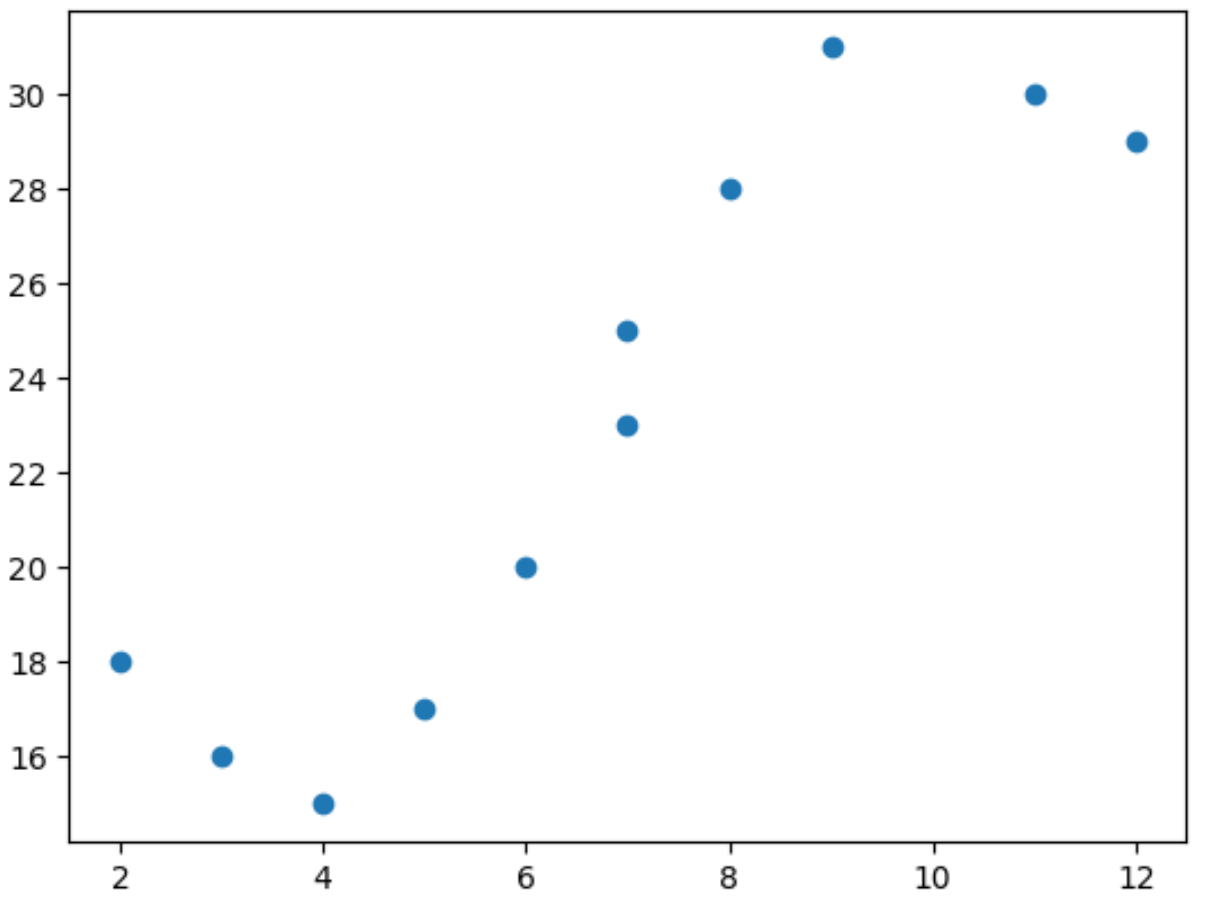
من مخطط التشتت، يمكننا أن نرى أن العلاقة بين x و y ليست خطية.

لذلك، من الجيد ملاءمة نموذج الانحدار متعدد الحدود مع البيانات لالتقاط العلاقة غير الخطية بين المتغيرين.

الخطوة 2: ملاءمة نموذج الانحدار متعدد الحدود

يوضح التعليمة البرمجية التالية كيفية استخدام وظائف sklearn لتناسب نموذج الانحدار متعدد الحدود من الدرجة 3 لمجموعة البيانات هذه:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

باستخدام معاملات النموذج الموضحة في الصف الأخير، يمكننا كتابة معادلة الانحدار متعدد الحدود المجهزة على النحو التالي:

ص = -0.109 ^س3 + 2.256س ² – 11.839س + 33.626

يمكن استخدام هذه المعادلة لإيجاد القيمة المتوقعة لمتغير الاستجابة بالنظر إلى قيمة معينة للمتغير المتوقع.

على سبيل المثال، إذا كانت x تساوي 4، فإن القيمة المتوقعة لمتغير الاستجابة y ستكون 15.39:

ص = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39

ملاحظة : لملاءمة نموذج الانحدار متعدد الحدود بدرجة مختلفة، ما عليك سوى تغيير قيمة وسيطة الدرجة في الدالة PolynomialFeatures() .

الخطوة 3: تصور نموذج الانحدار متعدد الحدود

أخيرًا، يمكننا إنشاء مخطط بسيط لتصور نموذج الانحدار متعدد الحدود الملائم لنقاط البيانات الأصلية:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

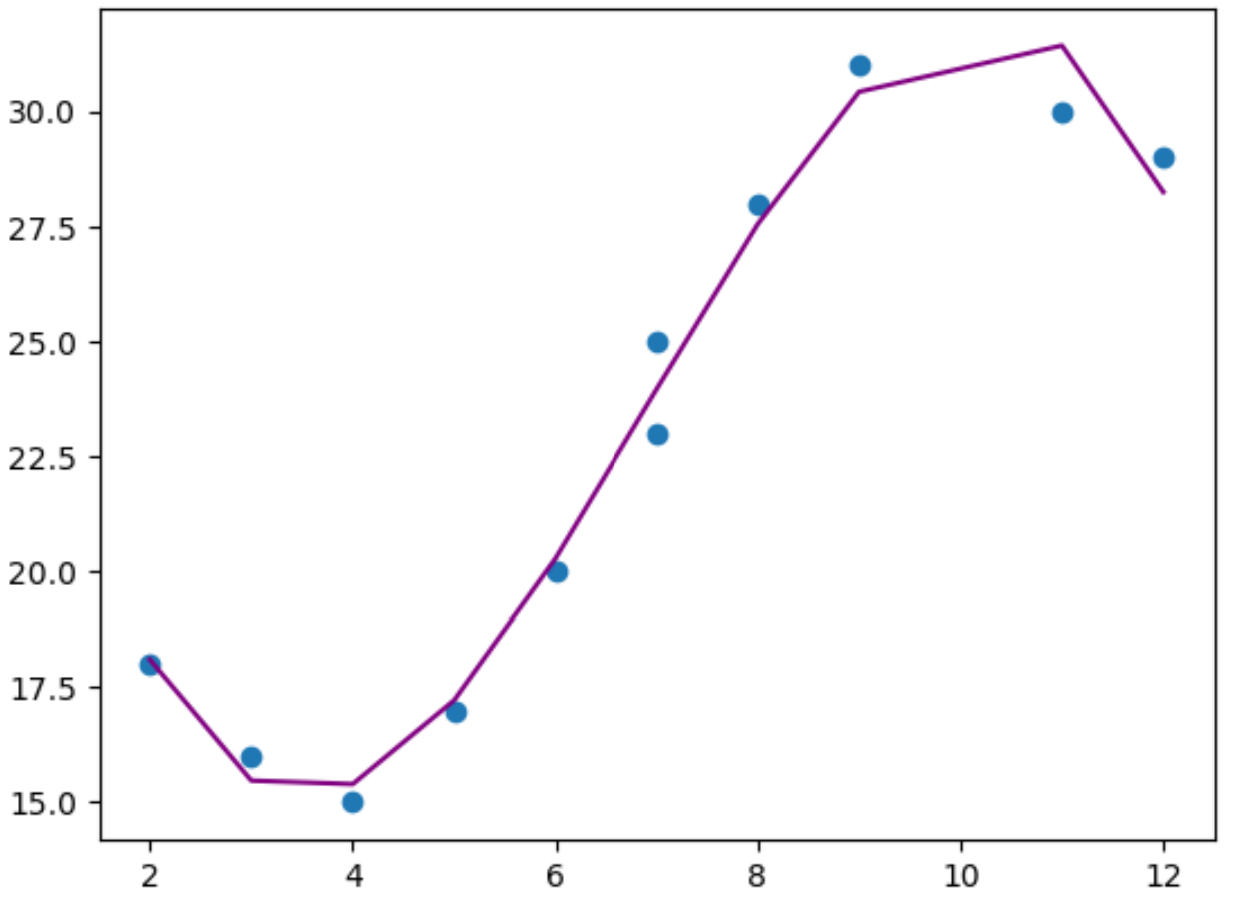
من الرسم البياني، يمكننا أن نرى أن نموذج الانحدار متعدد الحدود يبدو أنه يناسب البيانات بشكل جيد دون الإفراط في التجهيز .

ملاحظة : يمكنك العثور على الوثائق الكاملة لوظيفة sklearn PolynomialFeatures() هنا .

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى باستخدام sklearn:

كيفية استخراج معاملات الانحدار من sklearn
كيفية حساب الدقة المتوازنة باستخدام sklearn
كيفية تفسير تقرير التصنيف في Sklearn