كيفية إجراء الانحدار متعدد الحدود في بايثون

يستخدم تحليل الانحدار لتحديد العلاقة بين واحد أو أكثر من المتغيرات التوضيحية ومتغير الاستجابة.

النوع الأكثر شيوعًا لتحليل الانحدار هو الانحدار الخطي البسيط ، والذي يستخدم عندما يكون هناك علاقة خطية بين متغير التوقع ومتغير الاستجابة.

ومع ذلك، في بعض الأحيان تكون العلاقة بين متغير التوقع ومتغير الاستجابة غير خطية.

على سبيل المثال، قد تكون العلاقة الحقيقية تربيعية:

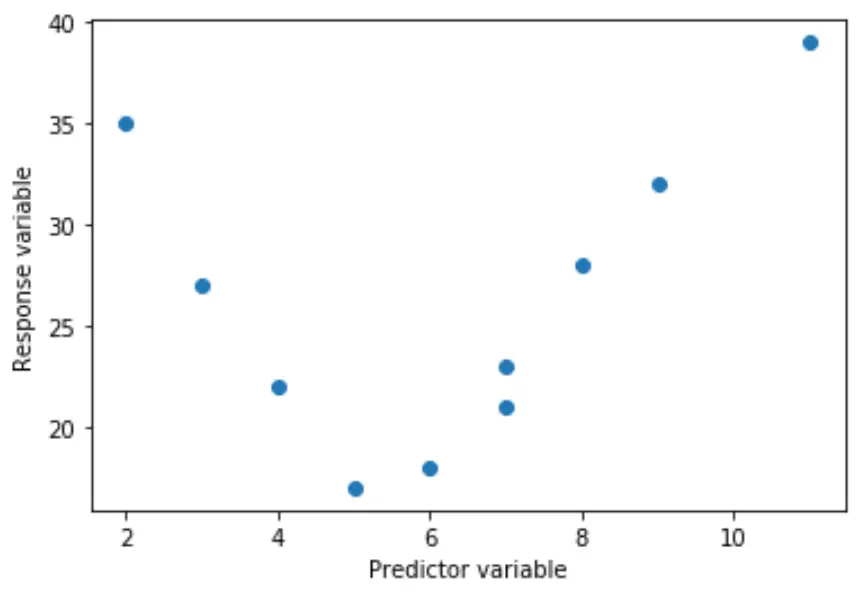
أو يمكن أن تكون مكعبة:

في هذه الحالات، من المنطقي استخدام الانحدار متعدد الحدود ، والذي يمكن أن يفسر العلاقة غير الخطية بين المتغيرات.

يشرح هذا البرنامج التعليمي كيفية تنفيذ الانحدار متعدد الحدود في بايثون.

مثال: الانحدار متعدد الحدود في بايثون

لنفترض أن لدينا متغير التوقع التالي (x) ومتغير الاستجابة (y) في بايثون:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

إذا أنشأنا مخططًا مبعثرًا بسيطًا لهذه البيانات، فيمكننا أن نرى أن العلاقة بين x وy ليست خطية بشكل واضح:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

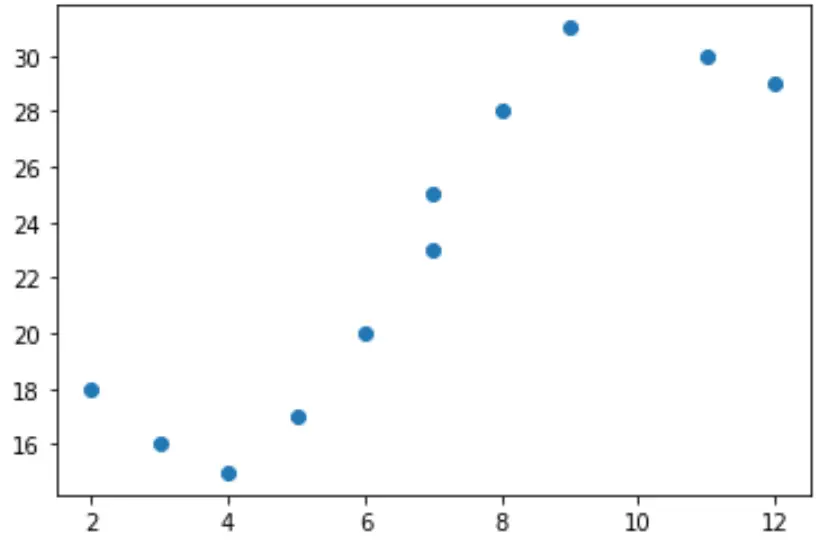
ولذلك لن يكون من المنطقي ملاءمة نموذج الانحدار الخطي مع هذه البيانات. بدلاً من ذلك، يمكننا محاولة ملاءمة نموذج الانحدار متعدد الحدود مع الدرجة 3 باستخدام الدالة numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

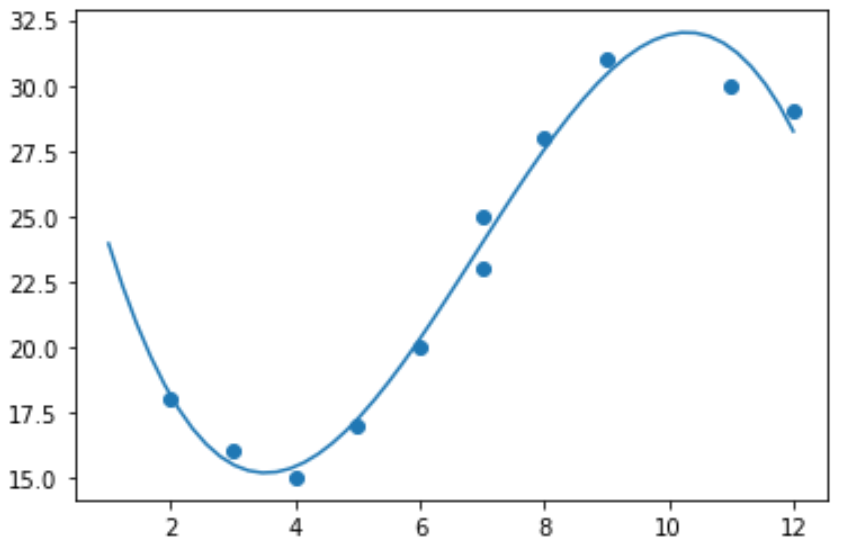
يمكننا الحصول على معادلة الانحدار متعدد الحدود المجهزة عن طريق طباعة معاملات النموذج:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

معادلة الانحدار متعدد الحدود المجهزة هي:

ص = -0.109 ^س3 + 2.256س ² – 11.839س + 33.626

يمكن استخدام هذه المعادلة لإيجاد القيمة المتوقعة لمتغير الاستجابة بمعلومية قيمة معينة للمتغير التوضيحي.

على سبيل المثال، افترض أن x = 4. القيمة المتوقعة لمتغير الاستجابة، y، ستكون:

ص = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39 .

يمكننا أيضًا كتابة دالة قصيرة للحصول على مربع R للنموذج، وهي نسبة التباين في متغير الاستجابة التي يمكن تفسيرها بواسطة المتغيرات المتوقعة.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

في هذا المثال، مربع R للنموذج هو 0.9841 .

وهذا يعني أن 98.41% من التباين في متغير الاستجابة يمكن تفسيره من خلال المتغيرات المتنبئة.