الانحدار أو التصنيف: ما هو الفرق؟

يمكن تقسيم خوارزميات التعلم الآلي إلى نوعين متميزين: خوارزميات التعلم الخاضعة للإشراف وغير الخاضعة للإشراف .

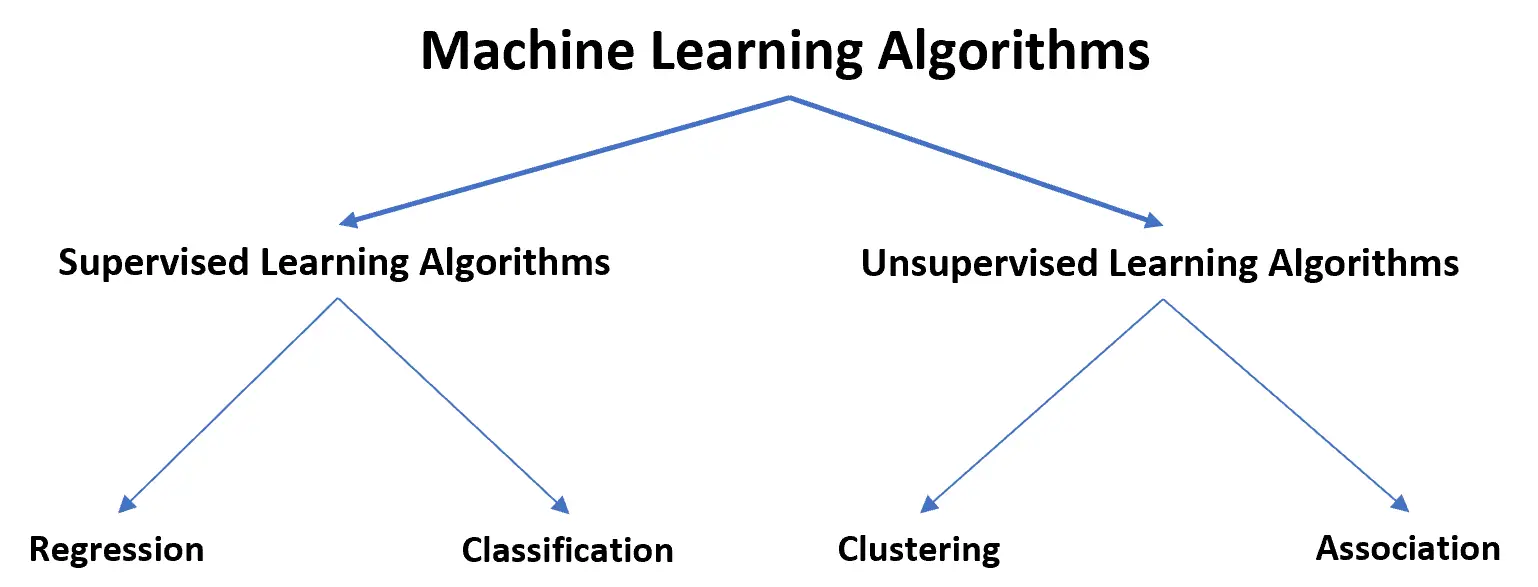
يمكن تصنيف خوارزميات التعلم الخاضعة للإشراف إلى نوعين:

1. الانحدار: متغير الاستجابة مستمر.

على سبيل المثال، يمكن أن يكون متغير الاستجابة :

• وزن
• ارتفاع
• سعر
• وقت
• إجمالي الوحدات

وفي كل حالة، يسعى نموذج الانحدار إلى التنبؤ بكمية مستمرة.

مثال الانحدار:

لنفترض أن لدينا مجموعة بيانات تحتوي على ثلاثة متغيرات لـ 100 منزل مختلف: المساحة المربعة، وعدد الحمامات، وسعر البيع.

يمكننا أن نلائم نموذج الانحدار الذي يستخدم المساحة المربعة وعدد الحمامات كمتغيرات توضيحية وسعر البيع كمتغير الاستجابة.

يمكننا بعد ذلك استخدام هذا النموذج للتنبؤ بسعر بيع المنزل، بناءً على المساحة المربعة وعدد الحمامات.

وهذا مثال لنموذج الانحدار لأن متغير الاستجابة (سعر البيع) مستمر.

الطريقة الأكثر شيوعًا لقياس دقة نموذج الانحدار هي حساب جذر متوسط مربع الخطأ (RMSE)، وهو مقياس يخبرنا بمدى اختلاف قيمنا المتوقعة عن قيمنا المرصودة في النموذج، في المتوسط. يتم حسابه على النحو التالي:

RMSE = √ Σ(P _i – O _i ) ² / n

ذهب:

• Σ هو رمز خيالي يعني “المجموع”
• P _i هي القيمة المتوقعة للملاحظة ^رقم
• O _i هي القيمة المرصودة للملاحظة ^رقم
• n هو حجم العينة

كلما كان RMSE أصغر، كانت قدرة نموذج الانحدار على ملاءمة البيانات أفضل.

2. التصنيف: متغير الاستجابة قاطع.

على سبيل المثال، يمكن لمتغير الاستجابة أن يأخذ القيم التالية:

• ذكر أم أنثى
• تنجح أو تفشل
• منخفضة أو متوسطة أو عالية

في كل حالة، يسعى نموذج التصنيف إلى التنبؤ بتسمية الفئة.

مثال على التصنيف:

لنفترض أن لدينا مجموعة بيانات تحتوي على ثلاثة متغيرات لـ 100 لاعب كرة سلة جامعي مختلف: متوسط النقاط لكل لعبة، ومستوى القسم، وما إذا كانوا قد تم تجنيدهم في الدوري الاميركي للمحترفين أم لا.

يمكننا تكييف نموذج تصنيف يستخدم متوسط النقاط لكل لعبة ولكل مستوى قسم كمتغيرات توضيحية و”تمت صياغته” كمتغير للاستجابة.

يمكننا بعد ذلك استخدام هذا النموذج للتنبؤ بما إذا كان سيتم تجنيد لاعب معين في الدوري الاميركي للمحترفين أم لا بناءً على متوسط نقاطه لكل لعبة ومستوى القسم.

هذا مثال لنموذج التصنيف لأن متغير الاستجابة (“المكتوب”) قاطع. بمعنى آخر، يمكن أن تأخذ القيم في فئتين مختلفتين فقط: “مكتوبة” أو “غير مسودة”.

الطريقة الأكثر شيوعًا لقياس دقة نموذج التصنيف هي ببساطة حساب النسبة المئوية للتصنيفات الصحيحة التي أجراها النموذج:

الدقة = تصنيفات التصحيح / إجمالي عدد محاولات التصنيف * 100%

على سبيل المثال، إذا كان النموذج يحدد بشكل صحيح ما إذا كان اللاعب سيتم تجنيده في الدوري الاميركي للمحترفين 88 مرة من أصل 100 مرة محتملة، فإن دقة النموذج هي:

الدقة = (88/100) * 100% = 88%

كلما زادت الدقة، زادت قدرة نموذج التصنيف على التنبؤ بالنتائج.

أوجه التشابه بين الانحدار والتصنيف

تتشابه خوارزميات الانحدار والتصنيف بالطرق التالية:

• كلاهما عبارة عن خوارزميات تعلم خاضعة للإشراف، أي أن كلاهما يتضمن متغير استجابة.
• يستخدم كلاهما متغيرًا توضيحيًا واحدًا أو أكثر لإنشاء نماذج للتنبؤ بالاستجابة.
• يمكن استخدام كلاهما لفهم كيفية تأثير التغييرات في قيم المتغيرات التوضيحية على قيم متغير الاستجابة.

الاختلافات بين الانحدار والتصنيف

تختلف خوارزميات الانحدار والتصنيف بالطرق التالية:

• تسعى خوارزميات الانحدار إلى التنبؤ بالكمية المستمرة وتسعى خوارزميات التصنيف إلى التنبؤ بتسمية الفئة.
• تختلف كيفية قياس دقة نماذج الانحدار والتصنيف.

تحويل الانحدار إلى التصنيف

تجدر الإشارة إلى أنه يمكن تحويل مشكلة الانحدار إلى مشكلة تصنيف بمجرد تقسيم متغير الاستجابة إلى أجزاء.

على سبيل المثال، لنفترض أن لدينا مجموعة بيانات تحتوي على ثلاثة متغيرات: المساحة المربعة وعدد الحمامات وسعر البيع.

يمكننا بناء نموذج انحدار باستخدام المساحة المربعة وعدد الحمامات للتنبؤ بأسعار المبيعات.

ومع ذلك، يمكننا تقسيم سعر البيع إلى ثلاث فئات مختلفة:

• 80.000 دولار – 160.000 دولار: “سعر البيع منخفض”
• 161.000 دولار – 240.000 دولار: “متوسط سعر البيع”
• 241.000 دولار – 320.000 دولار: “سعر البيع مرتفع”

يمكننا بعد ذلك استخدام اللقطات المربعة وعدد الحمامات كمتغيرات توضيحية للتنبؤ بالفئة (منخفضة أو متوسطة أو عالية) التي سيندرج فيها سعر بيع منزل معين.

سيكون هذا مثالاً لنموذج التصنيف لأننا نحاول وضع كل منزل في فصل دراسي.

ملخص

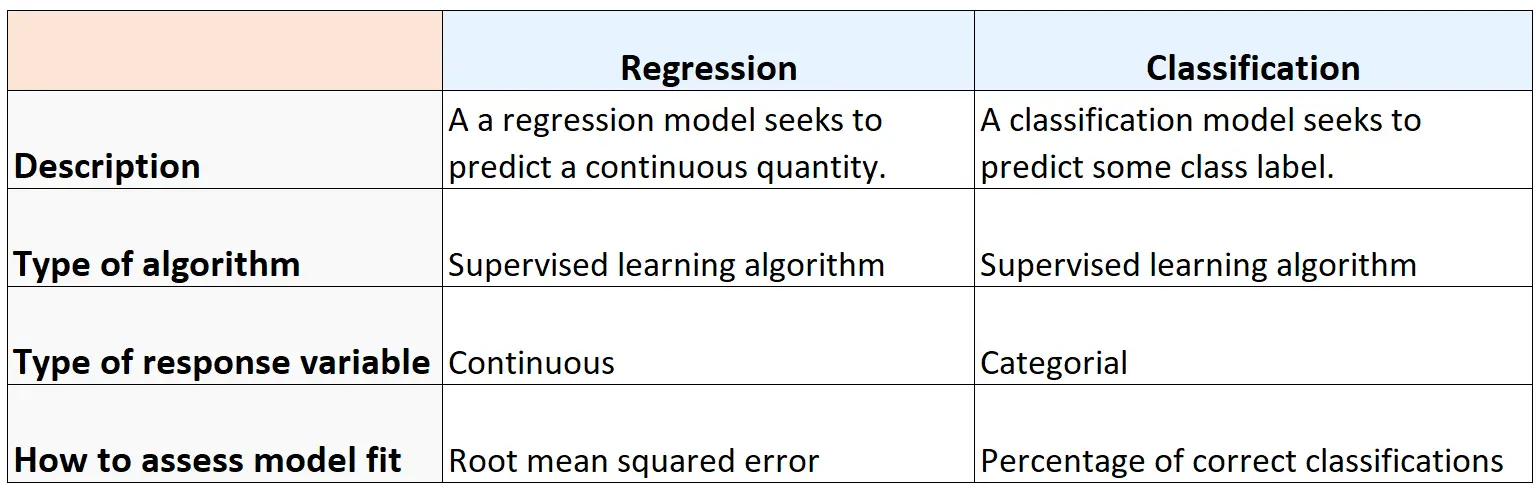
يلخص الجدول التالي أوجه التشابه والاختلاف بين خوارزميات الانحدار والتصنيف: