كيفية تفسير قطعة الأرض المتبقية المنحنية (مع مثال)

تُستخدم المخططات المتبقية لتقييم ما إذا كانت بقايا نموذج الانحدار موزعة بشكل طبيعي وما إذا كانت تظهر تغايرًا أم لا.

من الناحية المثالية، ترغب في أن تكون النقاط الموجودة في المخطط المتبقي متناثرة بشكل عشوائي حول قيمة صفر، بدون نمط واضح.

إذا واجهت مؤامرة متبقية حيث تحتوي نقاط الرسم على نمط منحني، فمن المحتمل أن يعني ذلك أن نموذج الانحدار الذي حددته للبيانات غير صحيح.

في معظم الحالات، يعني هذا أنك حاولت ملاءمة نموذج الانحدار الخطي مع مجموعة بيانات تتبع اتجاهًا تربيعيًا بدلاً من ذلك.

يوضح المثال التالي كيفية تفسير (وتصحيح) المخطط المتبقي المنحني عمليًا.

مثال: تفسير قطعة الأرض المتبقية المنحنية

لنفترض أننا قمنا بجمع البيانات التالية عن عدد ساعات العمل أسبوعيًا ومستوى السعادة المُبلغ عنه (على مقياس من 0 إلى 100) لـ 11 شخصًا مختلفًا في المكتب:

إذا أنشأنا مخططًا مبعثرًا بسيطًا لساعات العمل مقابل مستوى السعادة، فهذا هو الشكل الذي سيبدو عليه:

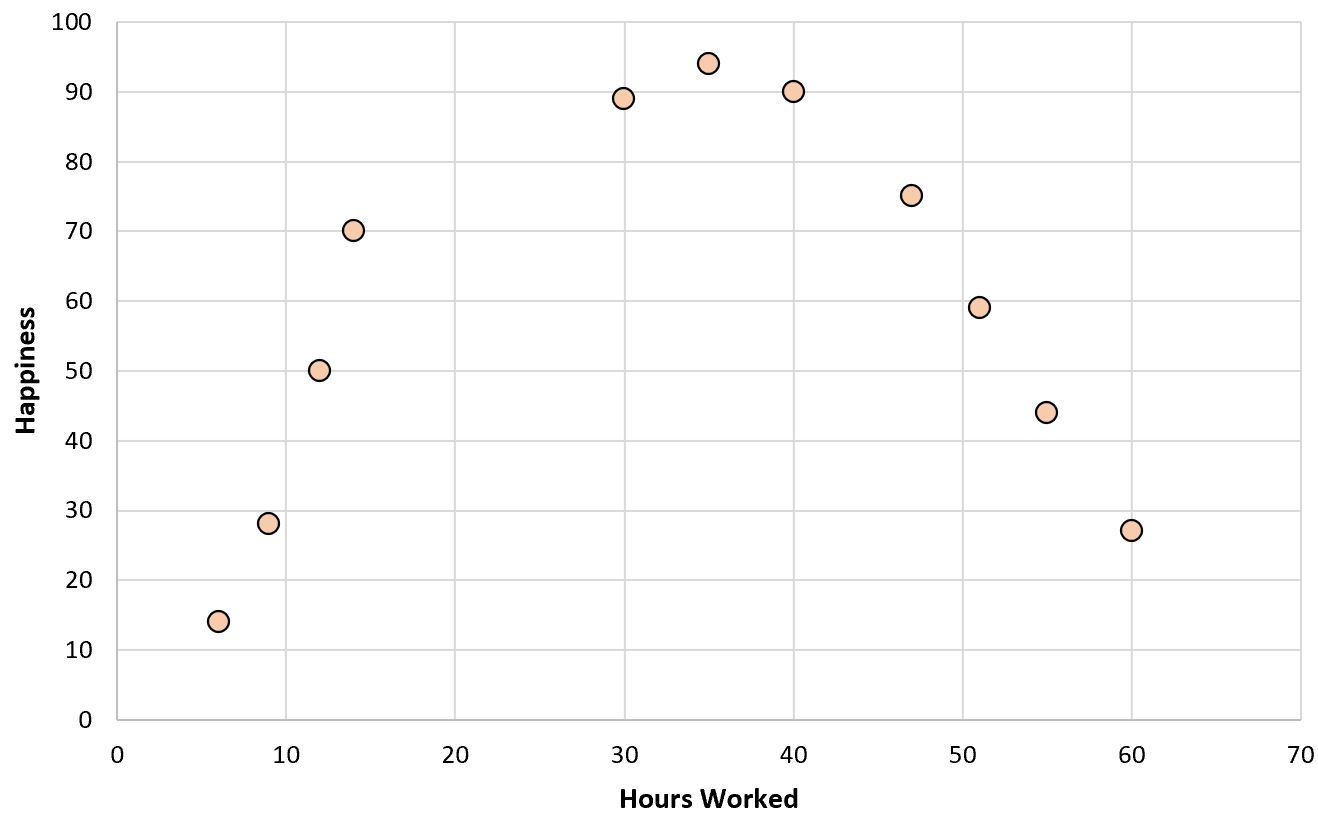
لنفترض الآن أننا نريد ملاءمة نموذج الانحدار باستخدام ساعات العمل للتنبؤ بمستويات السعادة.

يوضح التعليمة البرمجية التالية كيفية ملاءمة نموذج الانحدار الخطي البسيط لمجموعة البيانات هذه وإنتاج مخطط متبقي في R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

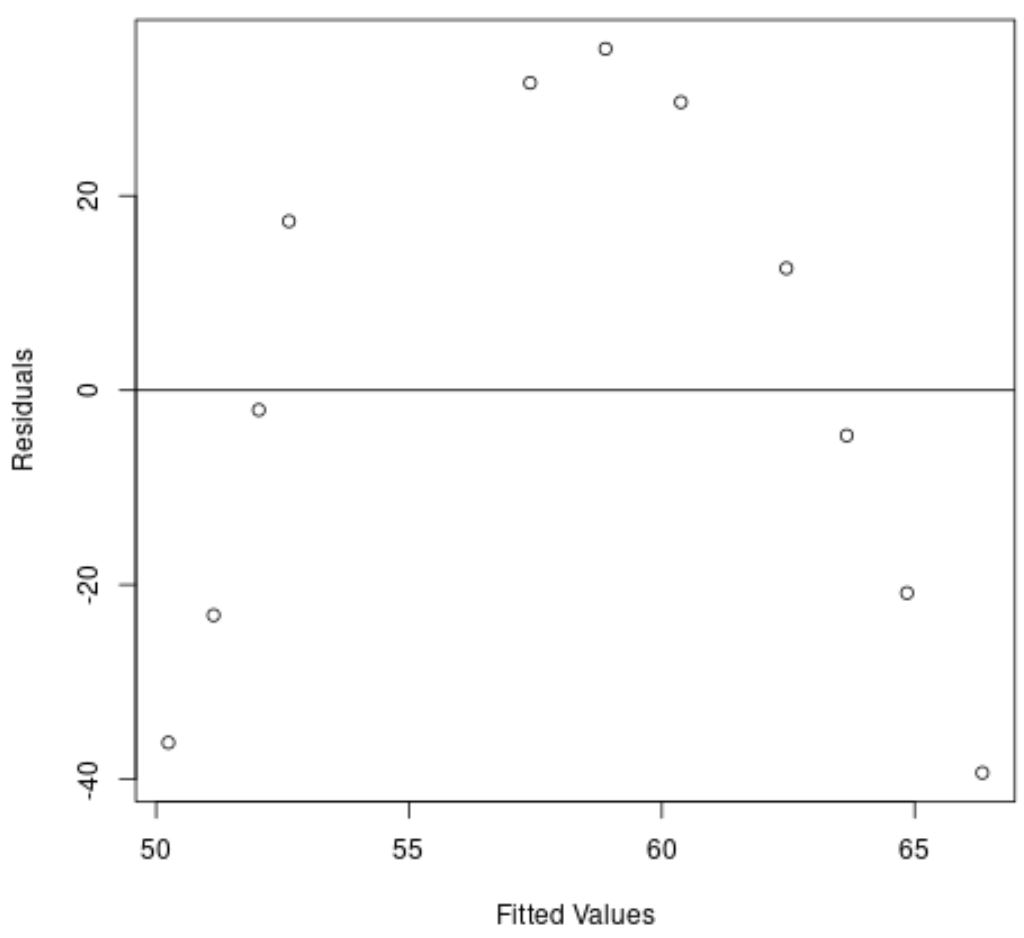
يعرض المحور السيني القيم المجهزة ويعرض المحور الصادي القيم المتبقية.

من الرسم البياني، يمكننا أن نرى أن هناك نمطًا منحنيًا في البقايا، مما يشير إلى أن نموذج الانحدار الخطي لا يوفر ملاءمة مناسبة لمجموعة البيانات هذه.

يوضح الكود التالي كيفية ملاءمة نموذج الانحدار التربيعي لمجموعة البيانات هذه وإنتاج مخطط متبقي في R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

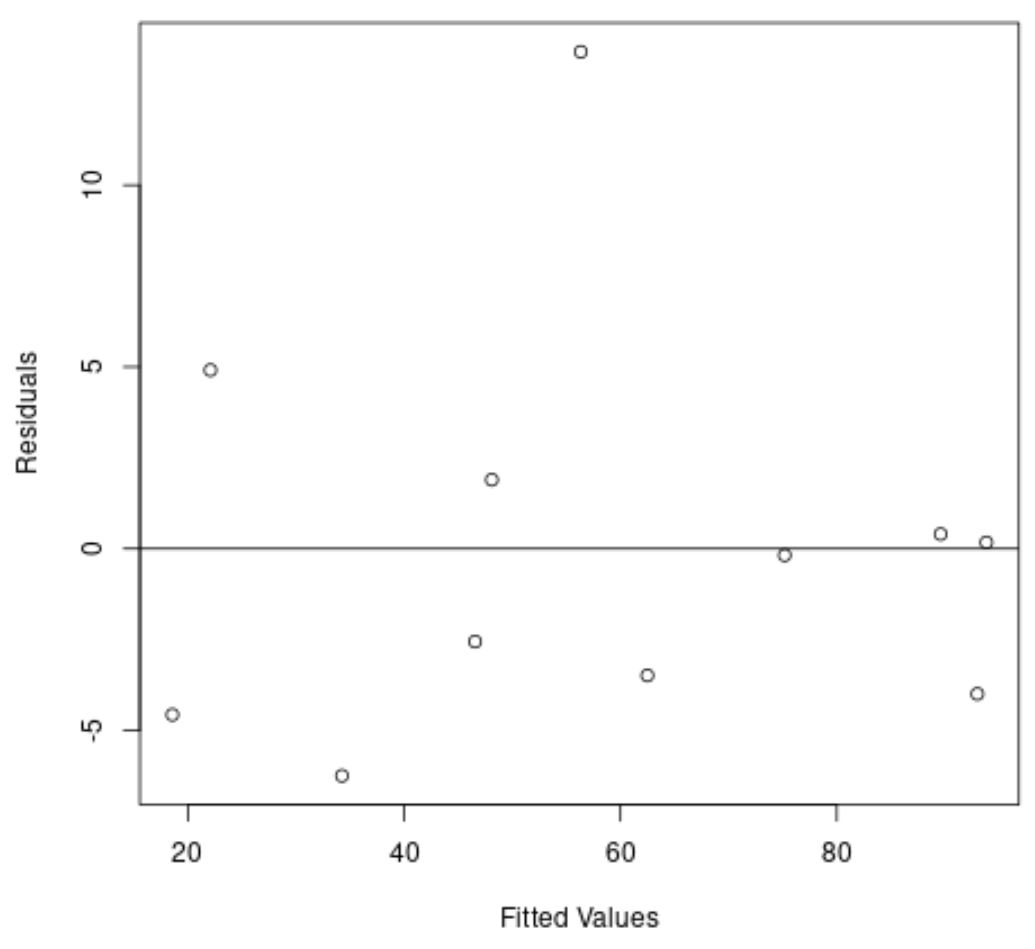
مرة أخرى، يوضح المحور السيني القيم المجهزة ويوضح المحور الصادي القيم المتبقية.

من المخطط يمكننا أن نرى أن البقايا متناثرة بشكل عشوائي حول الصفر ولا يوجد اتجاه واضح في البقايا.

يخبرنا هذا أن نموذج الانحدار التربيعي يقوم بعمل أفضل بكثير في ملاءمة مجموعة البيانات هذه من نموذج الانحدار الخطي.

يجب أن يكون هذا منطقيًا نظرًا لأننا رأينا أن العلاقة الحقيقية بين ساعات العمل ومستويات السعادة تبدو تربيعية وليست خطية.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إنشاء قطع أرض متبقية باستخدام برامج إحصائية مختلفة:

كيفية إنشاء المسار المتبقي باليد
كيفية إنشاء قطعة أرض متبقية في R
كيفية إنشاء مؤامرة المتبقية في إكسيل
كيفية إنشاء مؤامرة المتبقية في بيثون