الإحصائيات الوصفية أو الاستدلالية: ما الفرق؟

هناك فرعين رئيسيين في مجال الإحصاء:

• الإحصاء الوصفي
• الإحصائيات الاستدلالية

يشرح هذا البرنامج التعليمي الفرق بين الفرعين ولماذا يكون كل منهما مفيدًا في مواقف معينة.

الإحصائيات الوصفية

باختصار، يهدف الإحصاء الوصفي إلى وصف مجموعة من البيانات الأولية باستخدام الإحصائيات الموجزة والرسوم البيانية والجداول.

تعتبر الإحصائيات الوصفية مفيدة لأنها تسمح لك بفهم مجموعة من البيانات بسرعة وسهولة أكبر بكثير من مجرد النظر إلى صفوف وصفوف قيم البيانات الأولية.

على سبيل المثال، لنفترض أن لدينا مجموعة بيانات أولية توضح درجات اختبار 1000 طالب في مدرسة معينة. قد نكون مهتمين بمتوسط درجات الاختبار بالإضافة إلى توزيع درجات الاختبار.

باستخدام الإحصائيات الوصفية، يمكننا إيجاد متوسط الدرجات وإنشاء رسم بياني يساعدنا على تصور توزيع الدرجات.

يتيح لنا ذلك فهم درجات اختبار الطلاب بشكل أسهل بكثير من مجرد النظر إلى البيانات الأولية.

الأشكال الشائعة للإحصاءات الوصفية

هناك ثلاثة أشكال شائعة للإحصاءات الوصفية:

1. إحصائيات موجزة. هذه هي الإحصائيات التي تلخص البيانات باستخدام رقم واحد. هناك نوعان شائعان من الإحصائيات الموجزة:

• مقاييس النزعة المركزية : تصف هذه الأرقام مكان مركز مجموعة البيانات. وتشمل الأمثلة المتوسط   والوسيط .
• مقاييس التشتت: تصف هذه الأرقام توزيع القيم في مجموعة البيانات. تتضمن الأمثلة الفاصل الزمني والمدى الربيعي والانحراف المعياري والتباين .

2. الرسومات . تساعدنا الرسوم البيانية على تصور البيانات. تتضمن الأنواع الشائعة من المخططات المستخدمة لتصور البيانات المخططات المربعة ، والرسوم البيانية ، ومخططات الجذع والأوراق، والمخططات المبعثرة .

3. الجداول . يمكن أن تساعدنا الجداول في فهم كيفية توزيع البيانات. أحد أنواع الجداول الشائعة هو الجدول التكراري ، الذي يخبرنا بعدد قيم البيانات التي تقع ضمن نطاقات معينة.

مثال على استخدام الإحصاء الوصفي

يوضح المثال التالي كيف يمكننا استخدام الإحصائيات الوصفية في العالم الحقيقي.

لنفترض أن 1000 طالب في مدرسة معينة يأخذون نفس الاختبار. نريد أن نفهم توزيع نتائج الاختبار، لذلك نستخدم الإحصائيات الوصفية التالية:

1. إحصائيات موجزة

المتوسط : 82.13 . يخبرنا هذا أن متوسط درجات الاختبار بين 1000 طالب هو 82.13.

المتوسط: 84. وهذا يخبرنا أن نصف الطلاب حصلوا على درجات أعلى من 84 والنصف الآخر حصلوا على درجات أقل من 84.

الحد الأقصى: 100. الحد الأدنى: 45. هذا يخبرنا أن الحد الأقصى للدرجات التي حصل عليها أي طالب كان 100 والحد الأدنى للدرجات كان 45. النطاق – الذي يخبرنا بالفرق بين الحد الأقصى والحد الأدنى – هو 55.

2. الرسومات

لتصور توزيع نتائج الاختبار، يمكننا إنشاء رسم بياني – وهو نوع من المخططات التي تستخدم أشرطة مستطيلة لتمثيل الترددات.

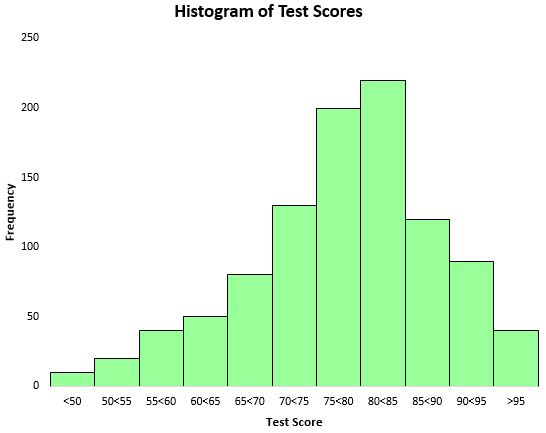
بناءً على هذا الرسم البياني، يمكننا أن نرى أن توزيع درجات الاختبار يكون على شكل جرس تقريبًا. حصل معظم الطلاب على درجات تتراوح بين 70 و90، بينما حصل عدد قليل جدًا منهم على درجات أعلى من 95 وأقل من ذلك على درجات أقل من 50.

3. الجداول

هناك طريقة أخرى سهلة لفهم توزيع الدرجات وهي إنشاء جدول تكراري. على سبيل المثال، يوضح الجدول التكراري التالي النسبة المئوية للطلاب الذين حصلوا على درجات بين نطاقات مختلفة:

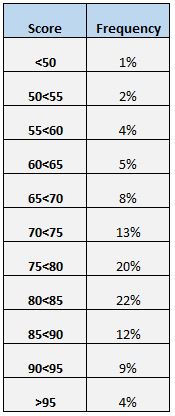
يمكننا أن نرى أن 4% فقط من إجمالي الطلاب حصلوا على درجة أعلى من 95. ويمكننا أيضًا أن نرى أن (12% + 9% + 4% =) 25% من جميع الطلاب حصلوا على 85 أو أعلى.

يعد الجدول التكراري مفيدًا بشكل خاص إذا أردنا معرفة النسبة المئوية لقيم البيانات التي تكون أعلى أو أقل من قيمة معينة. على سبيل المثال، لنفترض أن المدرسة تعتبر درجة الاختبار “المقبولة” هي أي درجة أعلى من 75.

بالنظر إلى الجدول التكراري، يمكننا أن نرى بسهولة أن (20% + 22% + 12% + 9% + 4% = ) 67% من الطلاب حصلوا على درجة مقبولة في الاختبار.

الإحصائيات الاستدلالية

باختصار، تستخدم الإحصائيات الاستدلالية عينة صغيرة من البيانات لاستخلاص استنتاجات حول العدد الأكبر من السكان الذي يتم سحب العينة منه.

على سبيل المثال، قد نرغب في فهم التفضيلات السياسية لملايين الأشخاص في بلد ما.

ومع ذلك، فإن إجراء مسح لكل فرد في البلاد سيكون مستهلكًا للوقت ومكلفًا للغاية. لذا، فإننا نفضل بدلاً من ذلك إجراء استطلاع أصغر على 1000 أمريكي، على سبيل المثال، واستخدام نتائج الاستطلاع لاستخلاص استنتاجات حول السكان ككل.

هذا هو الفرضية الكاملة للإحصاءات الاستدلالية: نريد الإجابة على سؤال حول السكان، لذلك نحصل على بيانات لعينة صغيرة من هؤلاء السكان ونستخدم بيانات العينة لاستخلاص استنتاجات حول السكان.

أهمية العينة التمثيلية

لكي نكون واثقين من قدرتنا على استخدام عينة لاستخلاص استنتاجات حول مجتمع ما، يجب علينا التأكد من أن لدينا عينة تمثيلية ، أي عينة تتطابق فيها خصائص الأفراد في المجتمع السكاني مع العينة بشكل وثيق صفات. من إجمالي عدد السكان.

ومن الناحية المثالية، نريد أن تشبه عينتنا “نسخة مصغرة” من سكاننا. وبالتالي، إذا أردنا استخلاص استنتاجات حول مجموعة من الطلاب تتكون من 50% فتيات و50% فتيان، فلن تكون عينتنا ممثلة إذا كانت تتضمن 90% فتيان و10% فتيات فقط.

إذا كانت عينتنا ليست مماثلة لإجمالي عدد السكان، فلا يمكننا بثقة تعميم نتائج العينة على إجمالي عدد السكان.

كيفية الحصول على عينة تمثيلية

لتعظيم فرص الحصول على عينة تمثيلية يجب التركيز على أمرين:

1. تأكد من استخدام طريقة أخذ العينات العشوائية.

هناك العديد من طرق أخذ العينات العشوائية التي يمكنك استخدامها والتي من المحتمل أن تنتج عينة تمثيلية، بما في ذلك:

• عينة عشوائية بسيطة
• عينة عشوائية منهجية
• عينة عشوائية عنقودية
• العينة العشوائية الطبقية

تميل طرق أخذ العينات العشوائية إلى إنتاج عينات تمثيلية لأن كل فرد من أفراد المجتمع لديه فرصة متساوية لإدراجه في العينة.

2. تأكد من أن حجم عينتك كبير بما يكفي .

بالإضافة إلى استخدام طريقة أخذ العينات المناسبة، من المهم التأكد من أن العينة كبيرة بما يكفي بحيث يكون لديك ما يكفي من البيانات لتتمكن من التعميم على عدد أكبر من السكان.

لتحديد حجم عينتك، عليك أن تأخذ في الاعتبار حجم المجتمع الذي تدرسه، ومستوى الثقة الذي تريد استخدامه، وهامش الخطأ الذي تعتبره مقبولاً.

لحسن الحظ، يمكنك استخدام الآلات الحاسبة عبر الإنترنت لإدخال هذه القيم ومعرفة حجم عينتك.

الأشكال الشائعة للإحصاءات الاستدلالية

هناك ثلاثة أشكال شائعة للإحصاءات الاستدلالية:

1. اختبار الفرضيات.

غالبًا ما نريد الإجابة على أسئلة حول مجموعة سكانية مثل:

• هل نسبة الأشخاص في ولاية أوهايو الذين يدعمون المرشح “أ” أكبر من 50%؟
• هل متوسط ارتفاع نبات معين يساوي 14 بوصة؟
• هل هناك فرق بين متوسط طول الطلاب في المدرسة (أ) والمدرسة (ب)؟

للإجابة على هذه الأسئلة، يمكننا إجراء اختبار الفرضيات ، والذي يسمح لنا باستخدام البيانات من عينة لاستخلاص استنتاجات حول السكان.

2. فترات الثقة .

في بعض الأحيان نريد تقدير قيمة معينة لعدد السكان. على سبيل المثال، قد نكون مهتمين بمتوسط ارتفاع نوع معين من النباتات في أستراليا.

بدلاً من التجول وقياس كل نبات في البلاد، يمكننا جمع عينة صغيرة من النباتات وقياس كل منها. ثم يمكننا استخدام متوسط ارتفاع النباتات في العينة لتقدير متوسط ارتفاع السكان.

ومع ذلك، من غير المرجح أن تقدم عينتنا تقديرًا مثاليًا لعدد السكان. ولحسن الحظ، يمكننا حساب عدم اليقين هذا من خلال إنشاء فاصل ثقة ، والذي يوفر نطاقًا من القيم التي نحن واثقون من أن المعلمة السكانية الحقيقية تقع ضمنها.

على سبيل المثال، يمكننا إنتاج فاصل ثقة بنسبة 95% يبلغ [13.2، 14.8]، مما يعني أننا متأكدون بنسبة 95% من أن متوسط الارتفاع الحقيقي لهذا النوع من النباتات يتراوح بين 13.2 بوصة و14.8 بوصة.

3. الانحدار .

في بعض الأحيان نريد أن نفهم العلاقة بين متغيرين في مجتمع ما.

على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كانت الساعات التي نقضيها في الدراسة أسبوعيًا مرتبطة بنتائج الاختبار . للإجابة على هذا السؤال، يمكننا تنفيذ تقنية تعرف باسم تحليل الانحدار .

لذلك، يمكننا أن ننظر إلى عدد الساعات المدروسة وكذلك درجات الاختبار لـ 100 طالب وإجراء تحليل الانحدار لمعرفة ما إذا كانت هناك علاقة ذات دلالة إحصائية بين المتغيرين.

إذا تبين أن القيمة p للانحدار مهمة ، فيمكننا أن نستنتج أن هناك علاقة ذات دلالة إحصائية بين هذين المتغيرين في إجمالي عدد الطلاب.

الفرق بين الإحصاء الوصفي والاستنتاجي

وباختصار، يمكن وصف الفرق بين الإحصاء الوصفي والاستنتاجي على النحو التالي:

تستخدم الإحصائيات الوصفية الإحصائيات الموجزة والرسوم البيانية والجداول لوصف مجموعة من البيانات.

وهذا مفيد لمساعدتنا على فهم مجموعة من البيانات بسرعة وسهولة دون المرور عبر جميع قيم البيانات الفردية.

تستخدم الإحصائيات الاستنتاجية العينات لاستخلاص استنتاجات حول أعداد أكبر من السكان.

اعتمادًا على السؤال الذي تريد الإجابة عليه حول المجتمع، قد تقرر استخدام واحدة أو أكثر من الطرق التالية: اختبار الفرضيات، وفترات الثقة، وتحليل الانحدار.

إذا اخترت استخدام إحدى هذه الطرق، فضع في اعتبارك أن عينتك يجب أن تكون ممثلة لسكانك ، وإلا فإن الاستنتاجات التي تستخلصها لن تكون موثوقة.