كيفية حساب المتوسط المتحرك الأسي في الباندا

في تحليل السلاسل الزمنية، المتوسط المتحرك هو ببساطة متوسط قيمة عدد من الفترات السابقة.

المتوسط المتحرك الأسي هو نوع من المتوسط المتحرك الذي يعطي أهمية أكبر للملاحظات الأخيرة، مما يعني أنه قادر على التقاط الاتجاهات الأخيرة بسرعة أكبر.

يشرح هذا البرنامج التعليمي كيفية حساب المتوسط المتحرك الأسي لعمود من القيم في pandas DataFrame.

مثال: المتوسط المتحرك الأسي في الباندا

لنفترض أن لدينا DataFrame الباندا التالية:

 import pandas as pd

#createDataFrame
df = pd.DataFrame({'period': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
                   'sales': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#view DataFrame 
df

        period sales
0 1 25
1 2 20
2 3 14
3 4 16
4 5 27
5 6 20
6 7 12
7 8 15
8 9 14
9 10 19

يمكننا استخدام الدالة pandas.DataFrame.ewm() لحساب المتوسط المتحرك المرجح بشكل كبير لعدد من الفترات السابقة.

على سبيل المثال، إليك كيفية حساب المتوسط المتحرك المرجح بشكل كبير باستخدام الفترات الأربع السابقة:

 #create new column to hold 4-day exponentially weighted moving average
df['4dayEWM'] = df['sales']. ewm (span= 4 , adjust= False ). mean ()

#view DataFrame 
df

        period sales 4dayEWM
0 1 25 25.000000
1 2 20 23.000000
2 3 14 19.400000
3 4 16 18.040000
4 5 27 21.624000
5 6 20 20.974400
6 7 12 17.384640
7 8 15 16.430784
8 9 14 15.458470
9 10 19 16.875082

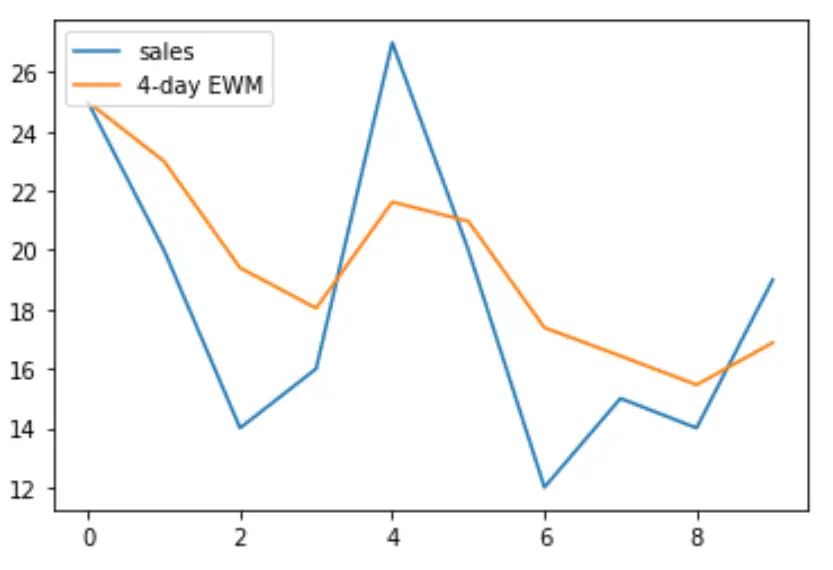
يمكننا أيضًا استخدام مكتبة matplotlib لتصور المبيعات مقارنة بالمتوسط المتحرك المرجح بشكل كبير لمدة 4 أيام:

 import matplotlib.pyplot as plt

#plot sales and 4-day exponentially weighted moving average
plt. plot (df['sales'], label='Sales')
plt. plot (df['4dayEWM'], label='4-day EWM')

#add legend to plot
plt. legend (loc=2)

مصادر إضافية

كيفية حساب المتوسطات المتحركة في بايثون
كيفية حساب متوسط الأعمدة في الباندا
كيفية حساب الارتباط التلقائي في بايثون