ما هي الفجوة المتبقية؟ (التعريف & #038؛ مثال)

يشير التباين المتبقي (يسمى أحيانًا “التباين غير المفسر”) إلى التباين في النموذج الذي لا يمكن تفسيره بواسطة متغيرات النموذج.

كلما زاد التباين المتبقي للنموذج، قلت قدرة النموذج على تفسير التباين في البيانات.

يظهر التباين المتبقي في نتائج نموذجين إحصائيين مختلفين:

1. تحليل التباين (ANOVA): يستخدم لمقارنة متوسطات ثلاث مجموعات مستقلة أو أكثر.

2. الانحدار: يستخدم لقياس العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .

توضح الأمثلة التالية كيفية تفسير التباين المتبقي في كل من هذه الطرق.

التباين المتبقي في نماذج ANOVA

في كل مرة نلائم نموذج ANOVA (“تحليل التباين”)، ينتهي بنا الأمر بجدول ANOVA الذي يبدو كما يلي:

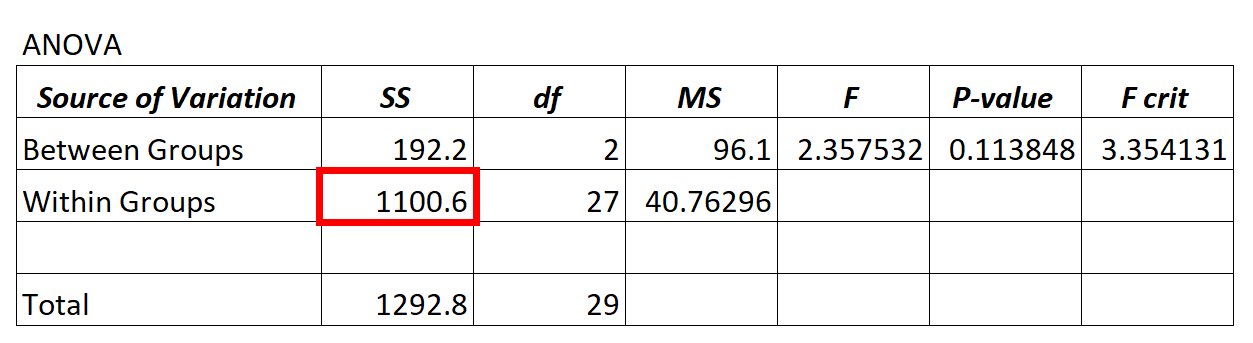
تم العثور على قيمة التباين المتبقية من نموذج ANOVA في عمود SS (“مجموع المربعات”) للتباين داخل المجموعة .

تسمى هذه القيمة أيضًا “مجموع الأخطاء المربعة” ويتم حسابها باستخدام الصيغة التالية:

Σ(X _ي – X _ي ) ²

ذهب:

• Σ : رمز يوناني معناه “المجموع”
• X _ij : الملاحظة ^{رقم 1} للمجموعة j
• X _j : متوسط المجموعة j

في نموذج ANOVA أعلاه، نرى أن التباين المتبقي هو 1100.6.

لتحديد ما إذا كان هذا التباين المتبقي “مرتفعًا”، يمكننا حساب متوسط مجموع المربعات داخل المجموعات ومتوسط مجموع المربعات بين المجموعات والعثور على النسبة بين الاثنين، مما يعطي قيمة F الإجمالية في جدول ANOVA.

• F = _دخول MS / _دخول MS
• ف = 96.1 / 40.76296
• ف = 2.357

قيمة F في جدول ANOVA أعلاه هي 2.357 والقيمة p المقابلة هي 0.113848. وبما أن هذه القيمة p لا تقل عن α = 0.05، فليس لدينا أدلة كافية لرفض فرضية العدم.

وهذا يعني أنه ليس لدينا أدلة كافية لنقول أن متوسط الفرق بين المجموعات التي نقارنها يختلف بشكل كبير.

يخبرنا هذا أن التباين المتبقي لنموذج ANOVA مرتفع مقارنة بالتباين الذي يمكن للنموذج تفسيره بالفعل.

التباين المتبقي في نماذج الانحدار

في نموذج الانحدار، يتم تعريف التباين المتبقي على أنه مجموع مربعات الاختلافات بين نقاط البيانات المتوقعة ونقاط البيانات المرصودة.

يتم حسابه على النحو التالي:

Σ(ŷ _i – y _i ) ²

ذهب:

• Σ : رمز يوناني معناه “المجموع”
• ŷ _i : نقاط البيانات المتوقعة
• y _i : نقاط البيانات المرصودة

عندما نلائم نموذج الانحدار، نحصل عادةً على نتيجة تبدو كما يلي:

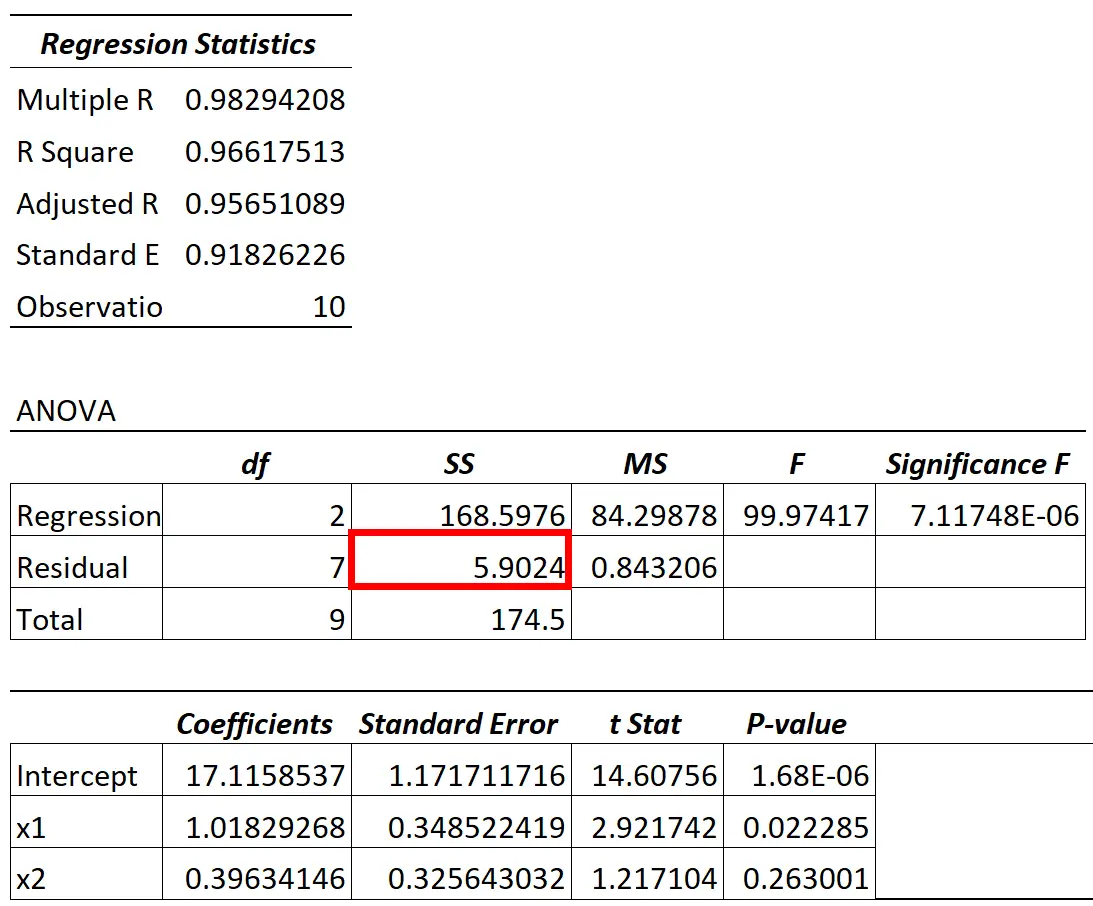
يمكن العثور على قيمة التباين المتبقية من نموذج ANOVA في عمود SS (“مجموع المربعات”) للتباين المتبقي.

تخبرنا نسبة التباين المتبقي إلى التباين الإجمالي في النموذج بنسبة التباين في متغير الاستجابة الذي لا يمكن تفسيره بواسطة المتغيرات المتوقعة في النموذج.

على سبيل المثال، في الجدول أعلاه، نحسب هذه النسبة على النحو التالي:

• الاختلاف غير المفسر = SS المتبقي / إجمالي SS
• التباين غير المفسر = 5.9024 / 174.5
• الاختلاف غير المفسر = 0.0338

ويمكن أيضًا حساب هذه القيمة باستخدام الصيغة التالية:

• التباين غير المفسر = 1 – R ²
• التباين غير المفسر = 1 – 0.96617
• الاختلاف غير المفسر = 0.0338

تخبرنا قيمة R-squared للنموذج بالنسبة المئوية للتباين في متغير الاستجابة الذي يمكن تفسيره بواسطة متغير التوقع.

وبالتالي، كلما انخفض التباين غير المفسر، زادت قدرة النموذج على استخدام المتغيرات المتوقعة لشرح التباين في متغير الاستجابة.

مصادر إضافية

ما هي قيمة R-squared الجيدة؟
كيفية حساب R-squared في إكسيل
كيفية حساب R-squared في R