كيفية إجراء القياس متعدد الأبعاد في بايثون
في الإحصاء، يعد القياس متعدد الأبعاد طريقة لتصور تشابه الملاحظات في مجموعة بيانات في الفضاء الديكارتي المجرد (عادةً الفضاء ثنائي الأبعاد).
أسهل طريقة لإجراء القياس متعدد الأبعاد في Python هي استخدام وظيفة MDS () للوحدة الفرعية sklearn.manifold .
يوضح المثال التالي كيفية استخدام هذه الوظيفة عمليًا.
مثال: القياس متعدد الأبعاد في بايثون
لنفترض أن لدينا DataFrame الباندا التالية التي تحتوي على معلومات حول مختلف لاعبي كرة السلة:
import pandas as pd #create DataFrane df = pd. DataFrame ({' player ': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K '], ' points ': [4, 4, 6, 7, 8, 14, 16, 19, 25, 25, 28], ' assists ': [3, 2, 2, 5, 4, 8, 7, 6, 8, 10, 11], ' blocks ': [7, 3, 6, 7, 5, 8, 8, 4, 2, 2, 1], ' rebounds ': [4, 5, 5, 6, 5, 8, 10, 4, 3, 2, 2]}) #set player column as index column df = df. set_index (' player ') #view Dataframe print (df) points assists blocks rebounds player A 4 3 7 4 B 4 2 3 5 C 6 2 6 5 D 7 5 7 6 E 8 4 5 5 F 14 8 8 8 G 16 7 8 10 H 19 6 4 4 I 25 8 2 3 D 25 10 2 2 K 28 11 1 2
يمكننا استخدام التعليمة البرمجية التالية لإجراء تحجيم متعدد الأبعاد باستخدام وظيفة MDS() الخاصة بوحدة sklearn.manifold :
from sklearn. manifold import MDS
#perform multi-dimensional scaling
mds = MDS(random_state= 0 )
scaled_df = mds. fit_transform (df)
#view results of multi-dimensional scaling
print (scaled_df)
[[ 7.43654469 8.10247222]
[4.13193821 10.27360901]
[5.20534681 7.46919526]
[6.22323046 4.45148627]
[3.74110999 5.25591459]
[3.69073384 -2.88017811]
[3.89092087 -5.19100988]
[ -3.68593169 -3.0821144 ]
[ -9.13631889 -6.81016012]
[ -8.97898385 -8.50414387]
[-12.51859044 -9.08507097]]
تم تقليل كل صف من DataFrame الأصلي إلى إحداثيات (x، y).
يمكننا استخدام الكود التالي لتصور هذه الإحداثيات في مساحة ثنائية الأبعاد:
import matplotlib.pyplot as plt #create scatterplot plt. scatter (scaled_df[:,0], scaled_df[:,1]) #add axis labels plt. xlabel (' Coordinate 1 ') plt. ylabel (' Coordinate 2 ') #add lables to each point for i, txt in enumerate( df.index ): plt. annotate (txt, (scaled_df[:,0][i]+.3, scaled_df[:,1][i])) #display scatterplot plt. show ()
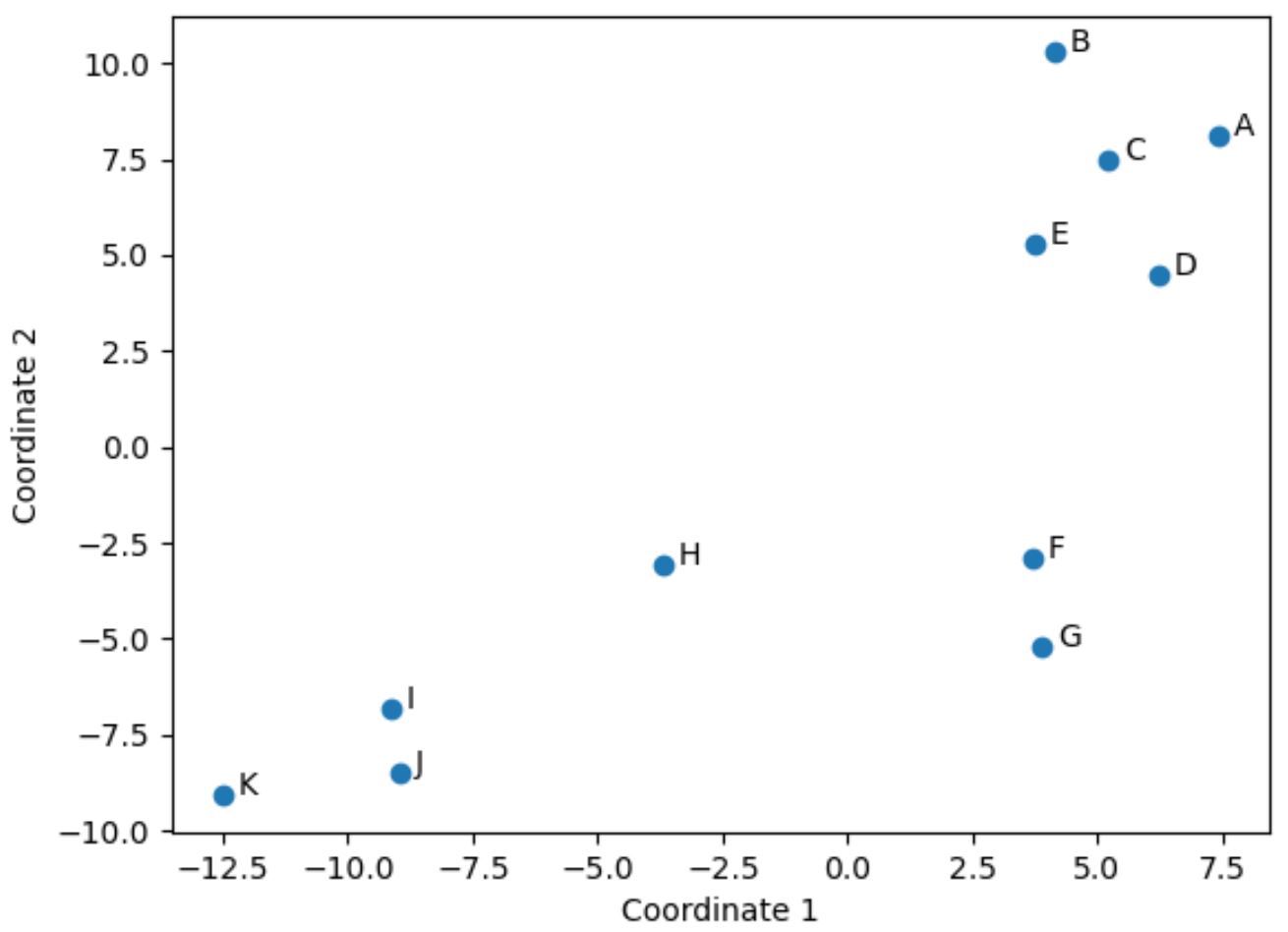
اللاعبون في DataFrame الأصلي الذين لديهم قيم مماثلة في الأعمدة الأربعة الأصلية (النقاط، التمريرات الحاسمة، الكتل، والمرتدات) قريبون من بعضهم البعض في المؤامرة.
على سبيل المثال، اللاعبان F و G قريبان من بعضهما البعض. فيما يلي قيمها من DataFrame الأصلي:
#select rows with index labels 'F' and 'G'
df. loc [[' F ',' G ']]
points assists blocks rebounds
player
F 14 8 8 8
G 16 7 8 10
إن قيم النقاط والتمريرات الحاسمة والكتل والمرتدات كلها متشابهة تمامًا، وهو ما يفسر سبب قربها من بعضها البعض في المخطط ثنائي الأبعاد.
في المقابل، خذ بعين الاعتبار اللاعبين B و K المتباعدين في الحبكة.
إذا أشرنا إلى قيمها في DataFrame الأصلي، يمكننا أن نرى أنها مختلفة تمامًا:
#select rows with index labels 'B' and 'K'
df. loc [[' B ',' K ']]
points assists blocks rebounds
player
B 4 2 3 5
K 28 11 1 2
لذا فإن الحبكة ثنائية الأبعاد هي طريقة جيدة لتصور مدى تشابه كل لاعب عبر جميع المتغيرات في DataFframe.
يتم تجميع اللاعبين ذوي الإحصائيات المتشابهة بالقرب من بعضهم البعض بينما يكون اللاعبون ذوو الإحصائيات المختلفة جدًا بعيدًا عن بعضهم البعض في المؤامرة.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في بايثون:
كيفية تطبيع البيانات في بايثون
كيفية إزالة القيم المتطرفة في بايثون
كيفية اختبار الحالة الطبيعية في بايثون