كيفية إجراء القياس متعدد الأبعاد في r (مع مثال)

في الإحصاء، يعد القياس متعدد الأبعاد طريقة لتصور تشابه الملاحظات في مجموعة بيانات في الفضاء الديكارتي المجرد (عادةً الفضاء ثنائي الأبعاد).

أسهل طريقة لإجراء القياس متعدد الأبعاد في R هي استخدام الدالة cmdscale() المضمنة، والتي تستخدم بناء الجملة الأساسي التالي:

cmdscale(d, eig = FALSE, k = 2, …)

ذهب:

• d : مصفوفة المسافة التي يتم حسابها بشكل عام بواسطة الدالة dist() .
• eig : ما إذا كان سيتم إرجاع القيم الذاتية أم لا.
• ك : عدد الأبعاد التي سيتم عرض البيانات فيها. الافتراضي هو 2 .

يوضح المثال التالي كيفية استخدام هذه الوظيفة عمليًا.

مثال: القياس متعدد الأبعاد في R

لنفترض أن لدينا إطار البيانات التالي في R الذي يحتوي على معلومات حول لاعبي كرة السلة المختلفين:

 #create data frame
df <- data. frame (points=c(4, 4, 6, 7, 8, 14, 16, 19, 25, 25, 28),
                 assists=c(3, 2, 2, 5, 4, 8, 7, 6, 8, 10, 11),
                 blocks=c(7, 3, 6, 7, 5, 8, 8, 4, 2, 2, 1),
                 rebounds=c(4, 5, 5, 6, 5, 8, 10, 4, 3, 2, 2))

#add row names
row. names (df) <- LETTERS[1:11]

#view data frame
df

  points assists blocks rebounds
A 4 3 7 4
B 4 2 3 5
C 6 2 6 5
D 7 5 7 6
E 8 4 5 5
F 14 8 8 8
G 16 7 8 10
H 19 6 4 4
I 25 8 2 3
D 25 10 2 2
K 28 11 1 2

يمكننا استخدام التعليمة البرمجية التالية لإجراء قياس متعدد الأبعاد باستخدام وظيفة cmdscale() وتصور النتائج في مساحة ثنائية الأبعاد:

 #calculate distance matrix
d <- dist(df)

#perform multidimensional scaling
fit <- cmdscale(d, eig= TRUE , k= 2 )

#extract (x, y) coordinates of multidimensional scaling
x <- fit$points[,1]
y <- fit$points[,2]

#create scatterplot
plot(x, y, xlab=" Coordinate 1 ", ylab=" Coordinate 2 ",
     main=" Multidimensional Scaling Results ", type=" n ")

#add row names of data frame as labels
text(x, y, labels=row. names (df))

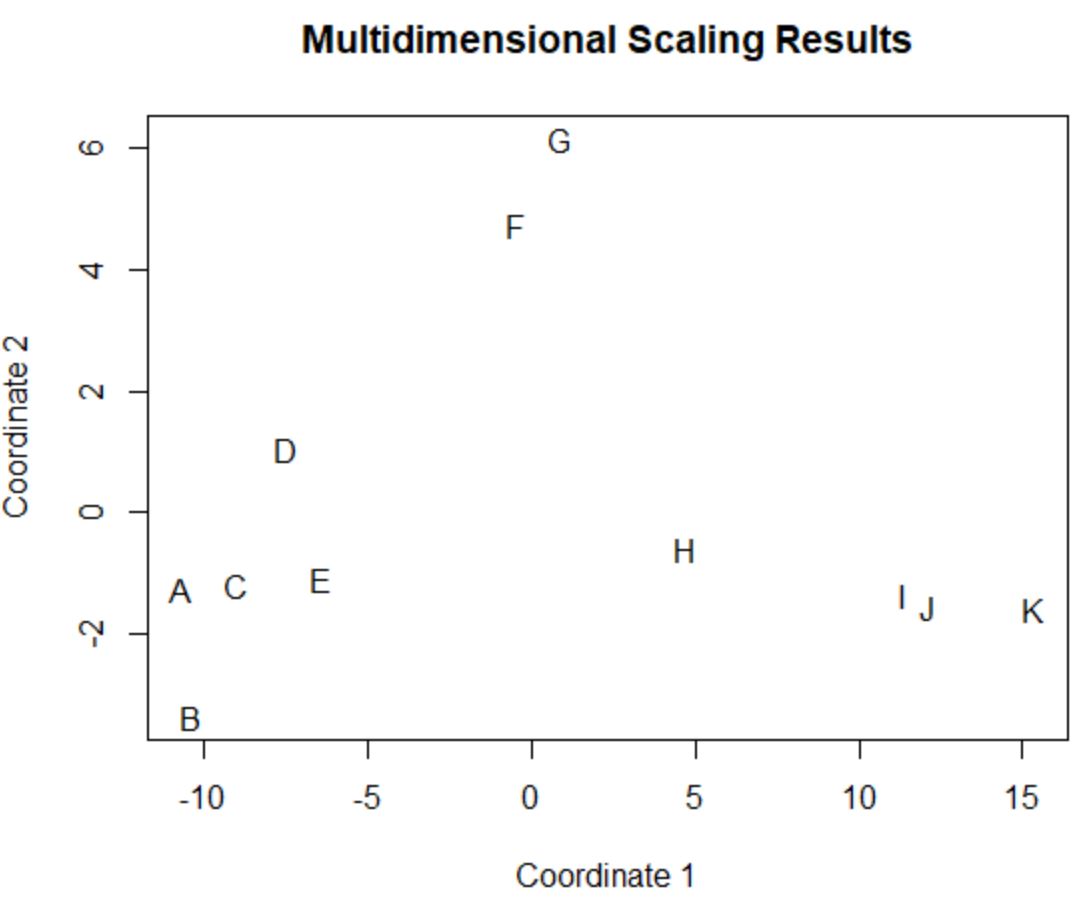
اللاعبون في إطار البيانات الأصلي الذين لديهم قيم متشابهة في الأعمدة الأربعة الأصلية (النقاط، التمريرات الحاسمة، الكتل، والمرتدات) قريبون من بعضهم البعض في المؤامرة.

على سبيل المثال، اللاعبان A و C قريبان من بعضهما البعض. فيما يلي قيمها من إطار البيانات الأصلي:

 #view data frame values for players A and C
df[rownames(df) %in% c(' A ', ' C '), ]

  points assists blocks rebounds
A 4 3 7 4
C 6 2 6 5

إن قيم النقاط والتمريرات الحاسمة والكتل والمرتدات كلها متشابهة تمامًا، وهو ما يفسر سبب قربها من بعضها البعض في المخطط ثنائي الأبعاد.

في المقابل، خذ بعين الاعتبار اللاعبين B و K المتباعدين في الحبكة.

إذا أشرنا إلى قيمها في البيانات الأصلية، يمكننا أن نرى أنها مختلفة تماما:

 #view data frame values for players B and K
df[rownames(df) %in% c(' B ', ' K '), ]

  points assists blocks rebounds
B 4 2 3 5
K 28 11 1 2

لذا فإن الرسم ثنائي الأبعاد يعد طريقة جيدة لتصور مدى تشابه كل لاعب عبر جميع المتغيرات في إطار البيانات.

يتم تجميع اللاعبين ذوي الإحصائيات المتشابهة بالقرب من بعضهم البعض بينما يكون اللاعبون ذوو الإحصائيات المختلفة جدًا بعيدًا عن بعضهم البعض في المؤامرة.

لاحظ أنه يمكنك أيضًا استخراج الإحداثيات الدقيقة (x، y) لكل لاعب في المخطط عن طريق كتابة fit ، وهو اسم المتغير الذي قمنا بتخزين نتائج الدالة cmdscale() فيه:

 #view (x, y) coordinates of points in the plot
fit

         [,1] [,2]
A -10.6617577 -1.2511291
B -10.3858237 -3.3450473
C -9.0330408 -1.1968116
D -7.4905743 1.0578445
E -6.4021114 -1.0743669
F -0.4618426 4.7392534
G 0.8850934 6.1460850
H 4.7352436 -0.6004609
I 11.3793381 -1.3563398
J 12.0844168 -1.5494108
K 15.3510585 -1.5696166

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في R:

كيفية تطبيع البيانات في R
كيفية مركز البيانات في R
كيفية إزالة القيم المتطرفة في R