التحليل أحادي المتغير أو متعدد المتغيرات: ما الفرق؟

يشير مصطلح التحليل أحادي المتغير إلى تحليل متغير واحد. يمكنك تذكر ذلك لأن البادئة “uni” تعني “واحد”.

يشير مصطلح التحليل متعدد المتغيرات إلى تحليل أكثر من متغير واحد. يمكنك تذكر ذلك لأن البادئة “متعدد” تعني “أكثر من واحد”.

هناك ثلاث طرق شائعة لإجراء التحليل أحادي المتغير :

1. إحصائيات موجزة

• يمكننا حساب مقاييس الاتجاه المركزي مثل المتوسط أو الوسيط للمتغير.
• يمكننا أيضًا حساب مقاييس التشتت مثل الانحراف المعياري للمتغير.

2. توزيعات التردد

• يمكننا إنشاء توزيع تكراري يصف عدد مرات ظهور كل قيمة للمتغير.

3. الرسومات

• يمكننا إنشاء رسوم بيانية مثل المخططات الصندوقية، والرسوم البيانية، ومخططات الكثافة، وما إلى ذلك. لتصور توزيع قيم المتغير.

هناك طريقتان شائعتان لإجراء التحليل متعدد المتغيرات :

1. مصفوفة مؤامرة مبعثر

• يمكننا إنشاء مصفوفة مخطط التشتت، والتي تسمح لنا بتصور العلاقة بين كل مجموعة زوجية من المتغيرات في مجموعة البيانات.

2. خوارزميات التعلم الآلي

• يمكننا استخدام خوارزمية التعلم الخاضع للإشراف لتناسب نموذجًا مثل الانحدار الخطي المتعدد الذي يحدد العلاقة بين متغيرات التوقع المتعددة ومتغير الاستجابة.
• يمكننا أيضًا استخدام خوارزمية التعلم غير الخاضعة للرقابة مثل تحليل المكونات الرئيسية للعثور في الوقت نفسه على البنية والعلاقات بين متغيرات متعددة في مجموعة البيانات.

توضح الأمثلة التالية كيفية إجراء تحليل أحادي المتغير ومتعدد المتغيرات باستخدام مجموعة البيانات التالية:

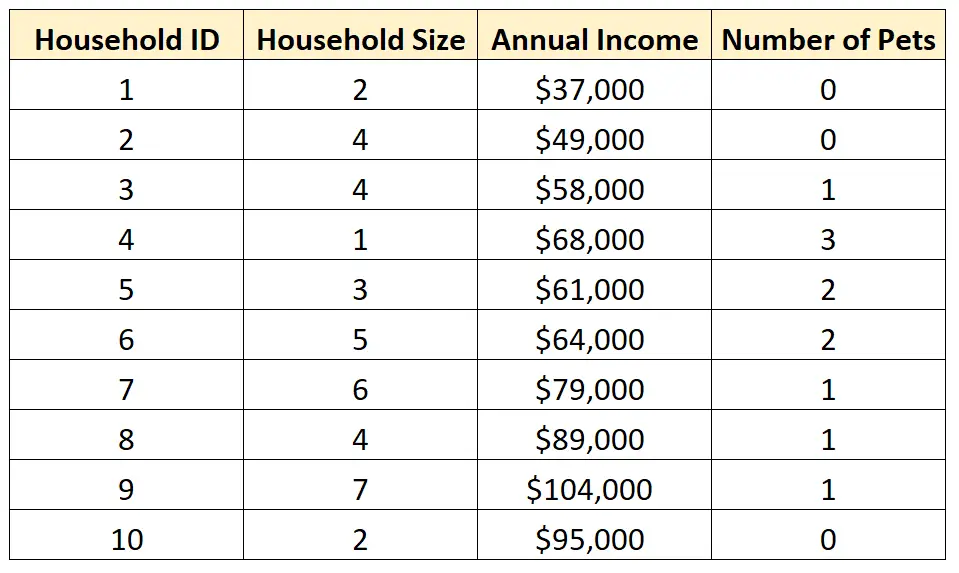
ملاحظة : عندما تقوم بتحليل متغيرين بالضبط، يسمى هذا التحليل ثنائي المتغير .

مثال: كيفية إجراء التحليل أحادي المتغير

يمكننا اختيار إجراء تحليل أحادي المتغير على أي من المتغيرات الفردية في مجموعة البيانات.

على سبيل المثال، يمكننا اختيار إجراء تحليل أحادي المتغير على المتغير حجم الأسرة :

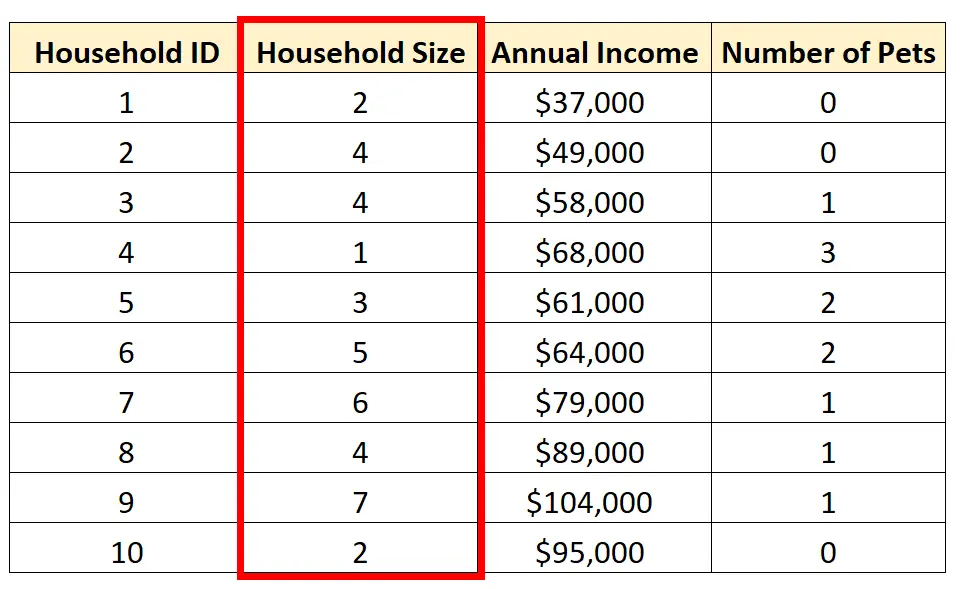
يمكننا حساب المقاييس التالية للاتجاه المركزي لحجم الأسرة:

• المتوسط (متوسط القيمة): 3.8
• الوسيط (القيمة المتوسطة): 4

تعطينا هذه القيم فكرة عن مكان وجود القيمة “المركزية”.

يمكننا أيضًا حساب مقاييس التشتت التالية:

• النطاق (الفرق بين الحد الأقصى والحد الأدنى): 6
• المقياس الرباعي (توزيع الـ 50% الوسطى من القيم): 2.5
• الانحراف المعياري (مقياس متوسط الانتشار): 1.87

هذه القيم تعطينا فكرة عن توزيع قيم هذا المتغير.

يمكننا أيضًا إنشاء جدول التوزيع التكراري التالي لتلخيص عدد مرات ظهور القيم المختلفة:

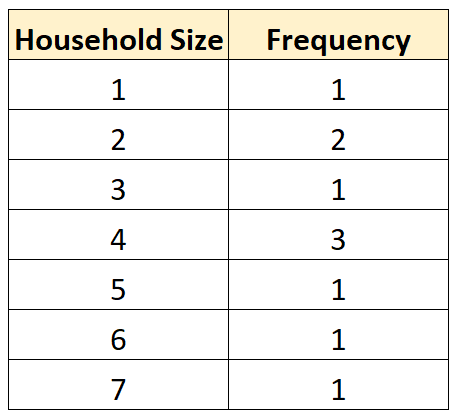
يمكننا أيضًا إنشاء مخطط boxplot لتصور توزيع القيم وفقًا لحجم الأسرة:

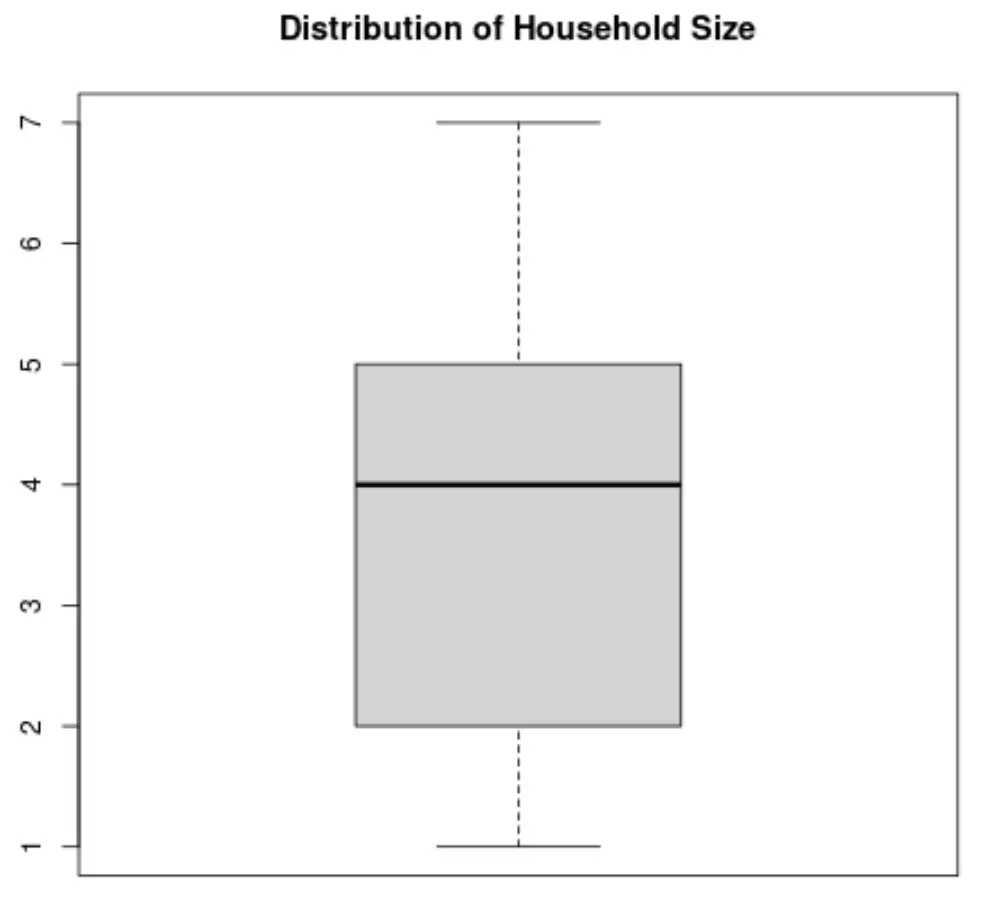
وبدلاً من ذلك، يمكننا إنشاء رسم بياني لتصور توزيع القيم:

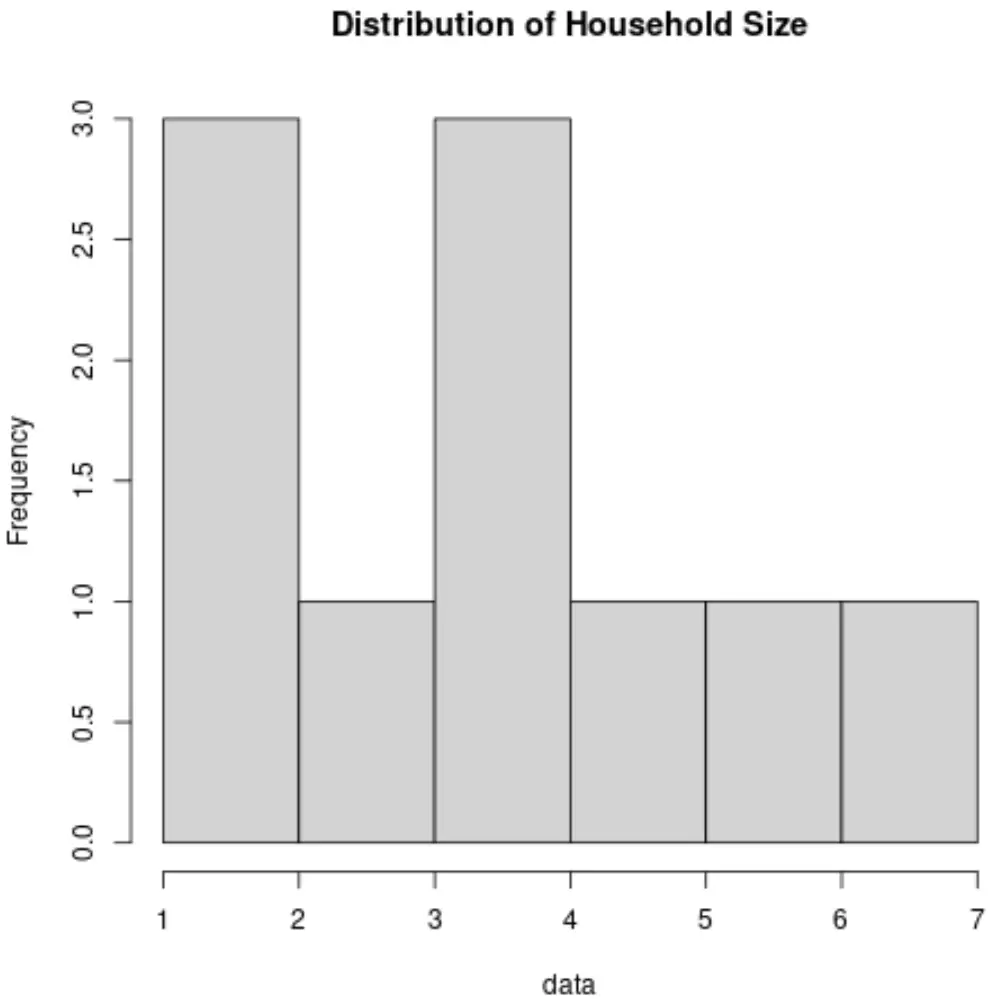
ومن خلال حساب هذه القياسات وإنشاء هذه الرسوم البيانية، يمكننا أن نفهم بشكل أفضل كيفية توزيع القيم لمتغير حجم الأسرة.

مثال: كيفية إجراء التحليل متعدد المتغيرات

لنفترض مرة أخرى أن لدينا نفس مجموعة البيانات:

أحد الأشكال البسيطة للتحليل متعدد المتغيرات الذي يمكننا إجراؤه على مجموعة البيانات هذه هو إنشاء مصفوفة مخطط التشتت ، وهي مصفوفة تعرض مخطط التشتت لكل مجموعة زوجية من المتغيرات الرقمية في مجموعة البيانات.

يمكننا إنشاء هذا النوع من المصفوفة لتصور العلاقة بين حجم الأسرة والدخل السنوي وعدد الحيوانات الأليفة في نفس الوقت.

المصدر : راجع هذا البرنامج التعليمي لمعرفة كيفية إنشاء مصفوفة مخطط التشتت في R.

هناك طريقة أخرى لإجراء تحليل متعدد المتغيرات على مجموعة البيانات هذه وهي ملاءمة نموذج الانحدار الخطي المتعدد . على سبيل المثال، يمكننا إنشاء نموذج انحداري يستخدم حجم الأسرة وعدد الحيوانات الأليفة للتنبؤ بالدخل السنوي.

المصدر : راجع هذا البرنامج التعليمي لمعرفة كيفية إجراء الانحدار الخطي المتعدد في R.

هناك طريقة أخرى لإجراء تحليل متعدد المتغيرات على مجموعة البيانات هذه وهي إجراء تحليل المكون الرئيسي ، والذي يسمح لنا بالعثور على البنية الأساسية في مجموعة البيانات.

المصدر : راجع هذا البرنامج التعليمي لمعرفة كيفية إجراء تحليل المكون الرئيسي في R.

خاتمة

فيما يلي ملخص موجز لهذه المقالة:

• التحليل أحادي المتغير هو تحليل متغير واحد.
• التحليل متعدد المتغيرات هو تحليل أكثر من متغير واحد.
• هناك طرق مختلفة لإجراء كل نوع من التحليلات اعتمادًا على هدفك النهائي.
• في العالم الحقيقي، غالبًا ما نقوم بإجراء كلا النوعين من التحليل على مجموعة بيانات واحدة.
• يتيح لنا التحليل أحادي المتغير فهم توزيع القيم للمتغير بينما يتيح لنا التحليل متعدد المتغيرات فهم العلاقة بين متغيرات متعددة.