كيفية حساب التكرار المتوقع

التكرار المتوقع هو التكرار النظري الذي نتوقع حدوثه في التجربة.

يظهر هذا النوع من التردد في أغلب الأحيان في نوعين من اختبارات مربع كاي:

• اختبار جودة المطابقة لمربع كاي
• اختبار مربع كاي للاستقلال

يشرح هذا البرنامج التعليمي كيفية حساب التكرارات المتوقعة لكل من هذين الاختبارين.

التكرار المتوقع في اختبار جودة المطابقة لمربع كاي

يتم استخدام اختبار جودة الملاءمة لمربع كاي لتحديد ما إذا كان المتغير القاطع يتبع توزيعًا افتراضيًا أم لا. في هذا النوع من الاختبارات، نقوم بمقارنة التكرارات المرصودة للمتغير الفئوي مع التكرارات المتوقعة.

على سبيل المثال، لنفترض أن صاحب متجر يدعي أن عددًا متساويًا من العملاء يأتون إلى متجره كل يوم من أيام الأسبوع. لاختبار هذه الفرضية، يقوم باحث مستقل بتسجيل عدد العملاء الذين يأتون إلى المتجر في أسبوع معين ويجد ما يلي:

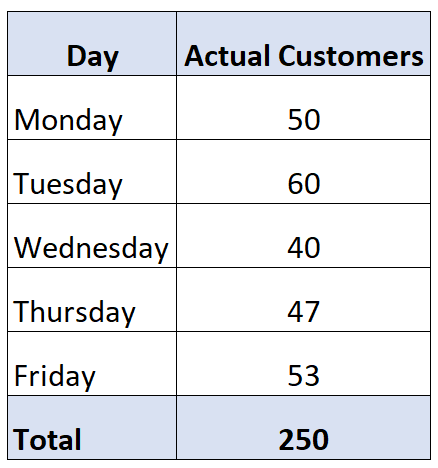
لحساب عدد العملاء المتوقع كل يوم، يمكننا استخدام الصيغة التالية:

التكرار المتوقع = النسبة المتوقعة * العدد الإجمالي

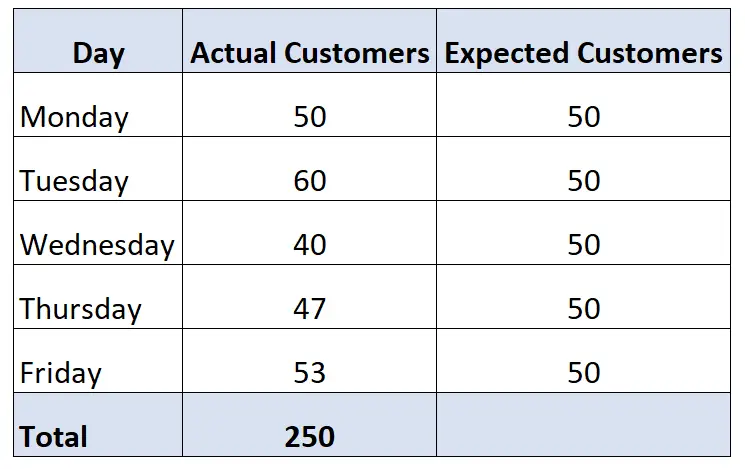
في هذا المثال تحديدًا، يتوقع مالك المتجر أن يدخل عدد متساوٍ من العملاء إلى المتجر كل يوم، وبالتالي فإن النسبة المئوية المتوقعة للعملاء الذين يأتون في يوم معين هي 20% من إجمالي عملاء الأسبوع.

وهذا يعني أنه يمكننا حساب التكرار المتوقع للعملاء كل يوم على النحو التالي:

التكرار المتوقع = 20% * 250 إجمالي العملاء = 50

التكرار المتوقع في اختبار كاي مربع للاستقلال

يتم استخدام اختبار مربع كاي للاستقلال لتحديد ما إذا كان هناك ارتباط كبير بين متغيرين فئويين أم لا. ومن خلال هذا النوع من الاختبارات، نقوم أيضًا بمقارنة مجموعة من التكرارات المرصودة مع مجموعة من التكرارات المتوقعة.

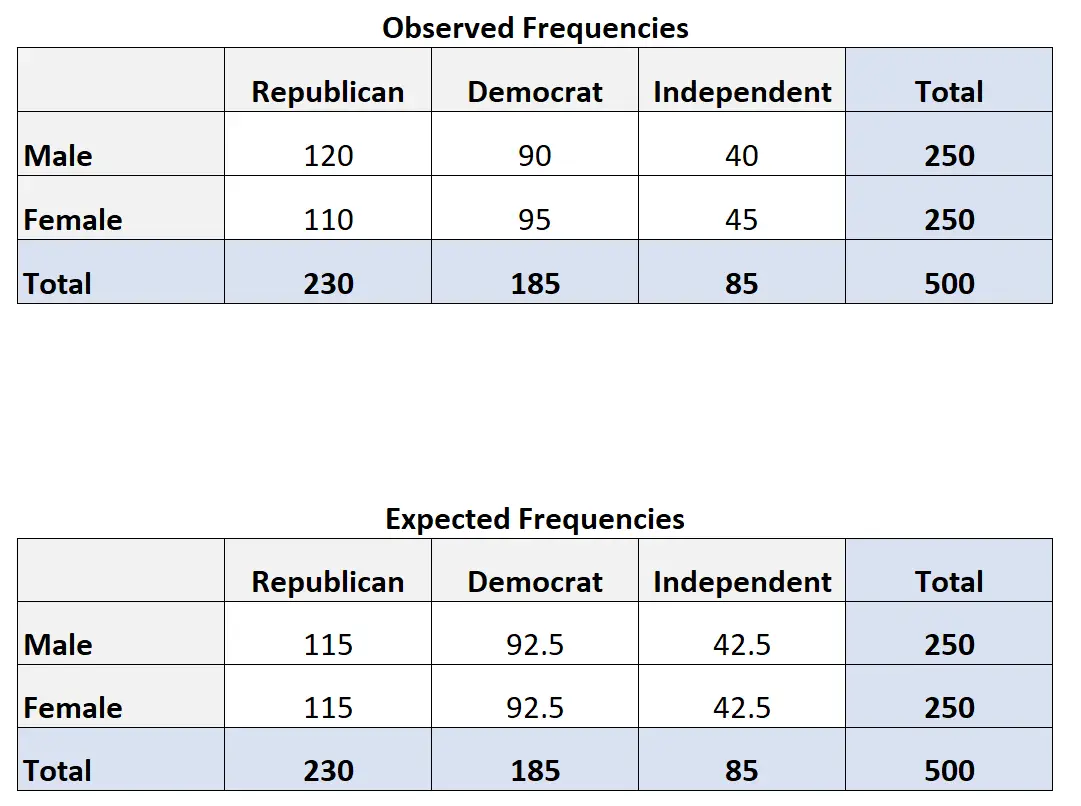
على سبيل المثال، لنفترض أننا نريد معرفة ما إذا كان الجنس مرتبطًا بتفضيل حزب سياسي أم لا. أخذنا عينة عشوائية بسيطة من 500 ناخب وسألناهم عن تفضيلاتهم الحزبية. ويعرض الجدول التالي نتائج الاستطلاع:

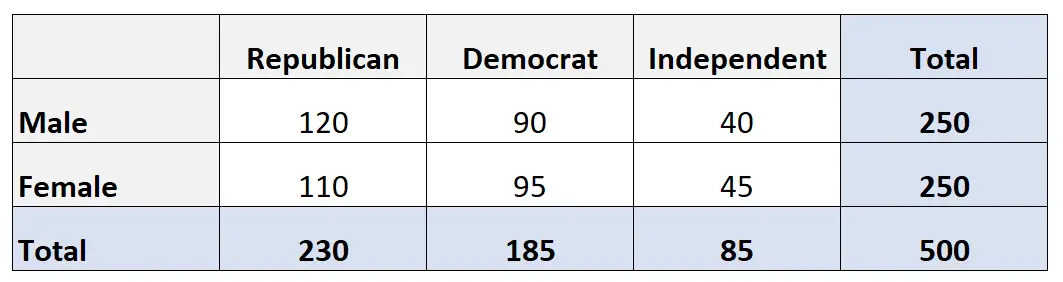
لحساب التكرار المتوقع لكل خلية في الجدول، يمكننا استخدام الصيغة التالية:

التكرار المتوقع = (مجموع الصفوف * مجموع الأعمدة) / مجموع الجدول

على سبيل المثال، القيمة المتوقعة للرجال الجمهوريين هي: (230*250) / 500 = 115 .

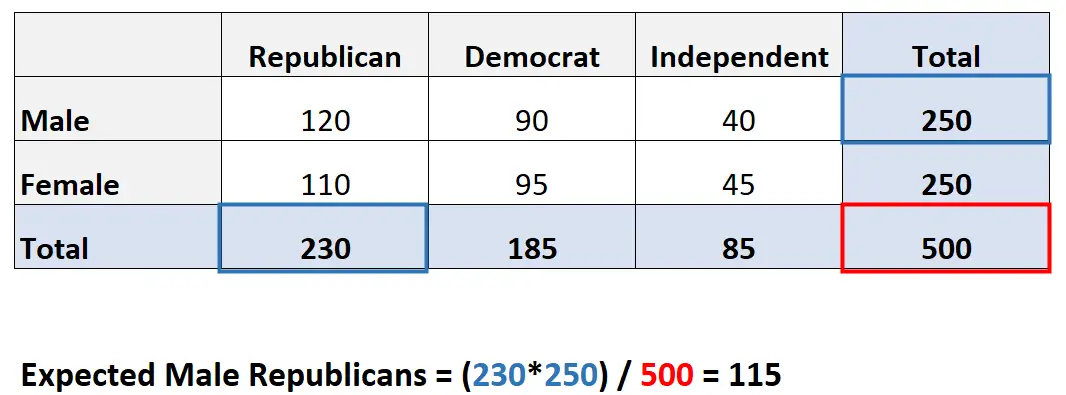
يمكننا تكرار هذه الصيغة للحصول على القيمة المتوقعة لكل خلية في الجدول:

يمكنك العثور على المزيد من دروس الإحصاء على صفحتنا هنا .