دليل كامل: التصميم العاملي 2×2

التصميم العاملي 2 × 2 هو نوع من التصميم التجريبي الذي يسمح للباحثين بفهم تأثيرات متغيرين مستقلين (كل منهما بمستويين ) على متغير تابع واحد.

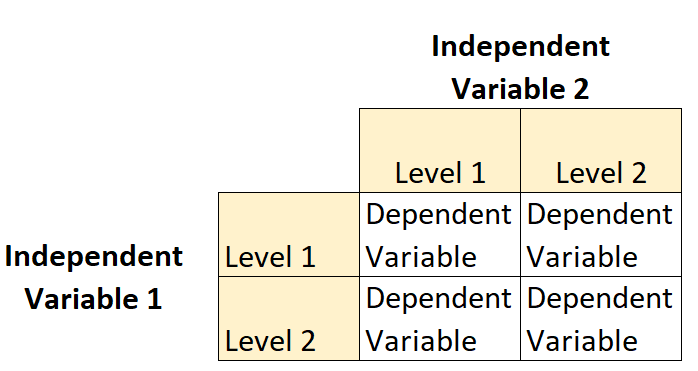
على سبيل المثال، لنفترض أن عالم النبات يريد فهم تأثيرات ضوء الشمس (المنخفض أو العالي) وتكرار الري (يوميًا أو أسبوعيًا) على نمو نوع نباتي معين.

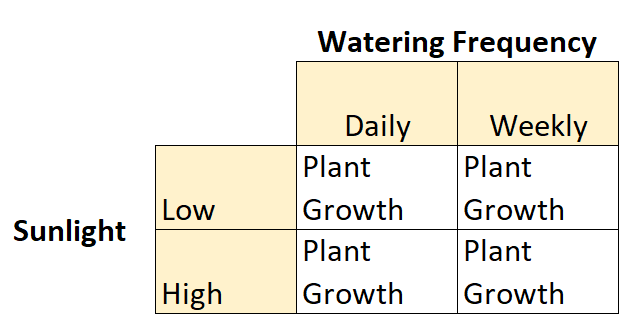
هذا مثال على التصميم العاملي 2×2 لأن هناك متغيرين مستقلين، لكل منهما مستويين:

• المتغير المستقل رقم 1: ضوء الشمس
  • المستويات: منخفضة، عالية
• المتغير المستقل رقم 2: تكرار الري
  • المستويات: يومي، أسبوعي

وهناك متغير تابع: نمو النبات.

الغرض من التصميم العاملي 2×2

يتيح التصميم العاملي 2×2 تحليل التأثيرات التالية:

التأثيرات الرئيسية: هي التأثيرات التي يحدثها متغير مستقل واحد على المتغير التابع.

على سبيل المثال، في السيناريو السابق، يمكننا تحليل التأثيرات الرئيسية التالية:

• التأثير الرئيسي لأشعة الشمس على نمو النبات.
  • يمكننا إيجاد متوسط نمو جميع النباتات التي تلقت ضوء الشمس المنخفض.
  • يمكننا إيجاد متوسط نمو جميع النباتات التي تلقت ضوء الشمس العالي.
• التأثير الرئيسي لتكرار الري على نمو النبات.
  • يمكننا العثور على متوسط نمو جميع النباتات التي تسقى يوميا.
  • يمكننا إيجاد متوسط نمو جميع النباتات التي يتم سقيها كل أسبوع.

تأثيرات التفاعل: تحدث عندما يعتمد تأثير متغير مستقل على المتغير التابع على مستوى المتغير المستقل الآخر.

على سبيل المثال، في السيناريو السابق، يمكننا تحليل تأثيرات التفاعل التالية:

• هل يعتمد تأثير ضوء الشمس على نمو النبات على عدد مرات الري؟
• هل تأثير تكرار الري على نمو النبات يعتمد على ضوء الشمس؟

تصور التأثيرات الرئيسية وتأثيرات التفاعل

عندما نستخدم التصميم العاملي 2 × 2، غالبًا ما نقوم برسم بياني للوسائل لفهم تأثيرات المتغيرات المستقلة على المتغير التابع بشكل أفضل.

على سبيل المثال، النظر في المؤامرة التالية:

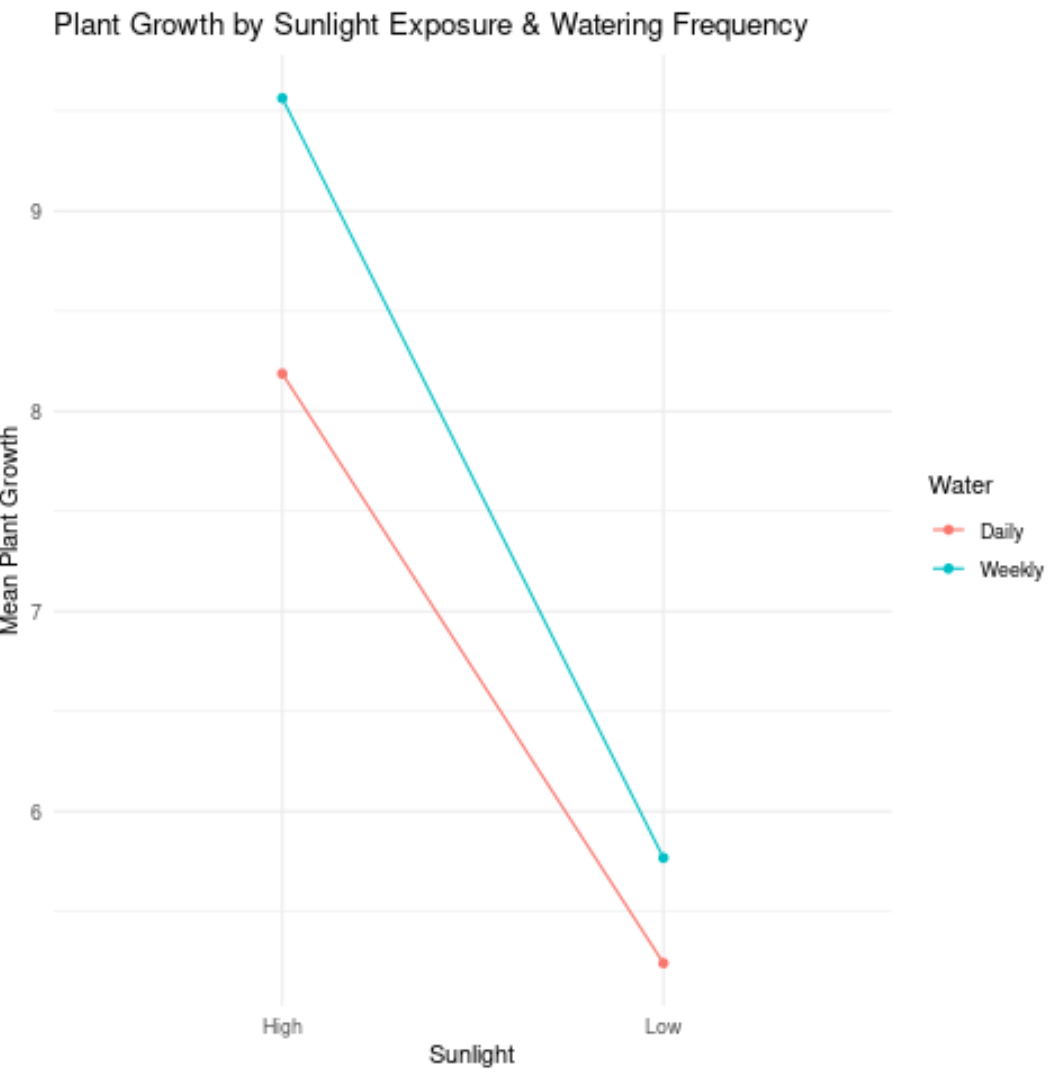
وإليك كيفية تفسير القيم في المؤامرة:

• وكان متوسط نمو النباتات التي تلقت أشعة الشمس الشديدة والري اليومي حوالي 8.2 بوصة.
• بلغ متوسط نمو النباتات التي تلقت أشعة الشمس العالية والري الأسبوعي حوالي 9.6 بوصة.
• وكان متوسط نمو النباتات التي تلقت أشعة الشمس المنخفضة والري اليومي حوالي 5.3 بوصة.
• كان متوسط نمو النباتات التي تلقت أشعة الشمس المنخفضة والري الأسبوعي حوالي 5.8 بوصة.

لتحديد ما إذا كان هناك تأثير تفاعل بين المتغيرين المستقلين، ما عليك سوى التحقق مما إذا كانت الخطوط متوازية أم لا:

• إذا كان خطا المؤامرة متوازيين، فلا يوجد تأثير للتفاعل.
• إذا كان خطا المؤامرة غير متوازيين، هناك تأثير التفاعل.

في الرسم البياني السابق، كان الخطان متوازيين تقريبًا، لذلك ربما لا يوجد تأثير تفاعل بين تكرار الري والتعرض للشمس.

ومع ذلك، النظر في المؤامرة التالية:

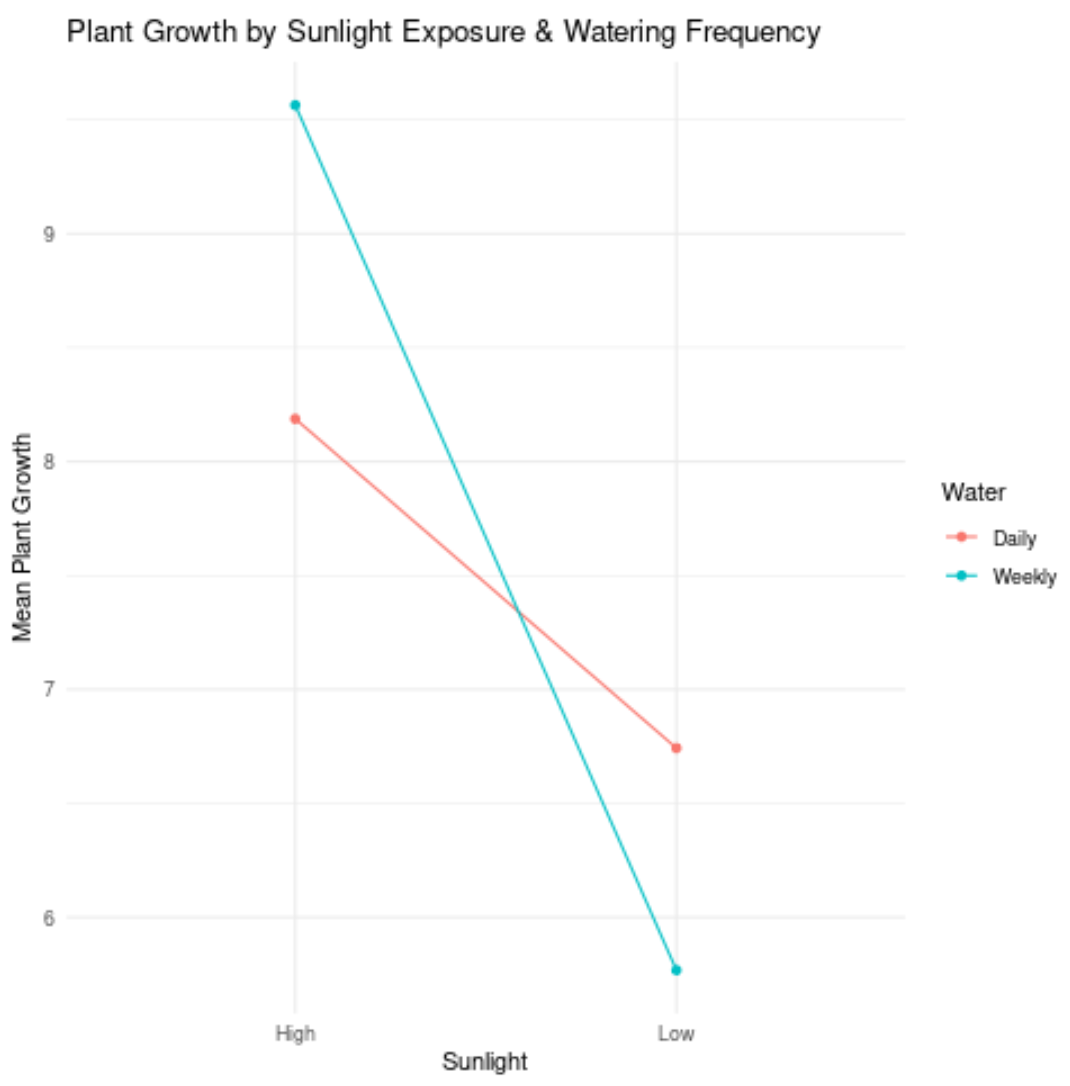
الخطان ليسا متوازيين على الإطلاق (في الحقيقة، هما متقاطعان!)، مما يدل على أنه من المحتمل أن يكون هناك تأثير تفاعل بينهما.

على سبيل المثال، هذا يعني أن تأثير ضوء الشمس على نمو النبات يعتمد على وتيرة الري.

بمعنى آخر، لا يؤثر ضوء الشمس وتكرار الري بشكل مستقل على نمو النبات. بل هناك تأثير تفاعل بين المتغيرين المستقلين.

كيفية تحليل التصميم العاملي 2×2

يعد رسم المتوسطات طريقة مرئية لفحص تأثيرات المتغيرات المستقلة على المتغير التابع.

ومع ذلك، يمكننا أيضًا إجراء تحليل التباين (ANOVA) ثنائي الاتجاه لاختبار ما إذا كانت المتغيرات المستقلة لها علاقة ذات دلالة إحصائية مع المتغير التابع أم لا.

على سبيل المثال، يوضح التعليمة البرمجية التالية كيفية إجراء ANOVA ثنائي الاتجاه لسيناريو المصنع الافتراضي الخاص بنا في R:

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

إليك كيفية تفسير نتيجة ANOVA:

• القيمة p المرتبطة بأشعة الشمس هي 0.005 . وبما أن هذا الرقم أقل من 0.05، فهذا يعني أن التعرض لأشعة الشمس له تأثير ذو دلالة إحصائية على نمو النبات.
• القيمة p المرتبطة بالماء هي 0.028 . وبما أن هذا الرقم أقل من 0.05، فهذا يعني أن تكرار الري له أيضًا تأثير ذو دلالة إحصائية على نمو النبات.
• القيمة p للتفاعل بين ضوء الشمس والماء هي 0.156 . وبما أن هذا الرقم لا يقل عن 0.05، فهذا يعني أنه لا يوجد تأثير تفاعل بين ضوء الشمس والماء.

مصادر إضافية

الدليل الكامل: التصميم العاملي 2 × 3
ما هي مستويات المتغير المستقل؟
المتغيرات المستقلة أو التابعة
ما هو عامل ANOVA؟