كيفية حساب الانحراف والتفرطح في r

في الإحصاء، يعد الانحراف والتفرطح طريقتين لقياس شكل التوزيع.

الانحراف هو مقياس لانحراف التوزيع. يمكن أن تكون هذه القيمة إيجابية أو سلبية.

• يشير الانحراف السلبي إلى أن الذيل يقع على الجانب الأيسر من التوزيع، والذي يمتد نحو قيم أكثر سلبية.
• يشير الانحراف الإيجابي إلى أن الذيل يقع على الجانب الأيمن من التوزيع، والذي يمتد نحو قيم أكثر إيجابية.
• تشير القيمة صفر إلى عدم وجود عدم تماثل في التوزيع، مما يعني أن التوزيع متماثل تمامًا.

التفرطح هو مقياس لمعرفة ما إذا كان التوزيع ثقيلا أو خفيفا مقارنة بالتوزيع الطبيعي .

• التفرطح للتوزيع الطبيعي هو 3.
• إذا كان توزيع معين يحتوي على تفرطح أقل من 3، فيقال أنه مسرحي ، مما يعني أنه يميل إلى إنتاج قيم متطرفة أقل وأقل تطرفًا من التوزيع الطبيعي.
• إذا كان توزيع معين يحتوي على تفرطح أكبر من 3، فيقال إنه تفرطح نحوي ، مما يعني أنه يميل إلى إنتاج قيم متطرفة أكثر من التوزيع الطبيعي.

ملحوظة: بعض الصيغ (تعريف فيشر) تطرح 3 من التفرطح لتسهيل مقارنته بالتوزيع الطبيعي. باستخدام هذا التعريف، سيكون للتوزيع تفرطح أكبر من التوزيع الطبيعي إذا كانت قيمة التفرطح أكبر من 0.

يشرح هذا البرنامج التعليمي كيفية حساب كل من الانحراف والتفرطح لمجموعة بيانات معينة في R.

مثال: الانحراف والتسطيح في R

لنفترض أن لدينا مجموعة البيانات التالية:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

يمكننا تصور توزيع القيم في مجموعة البيانات هذه بسرعة عن طريق إنشاء رسم بياني:

 hist(data, col=' steelblue ') 

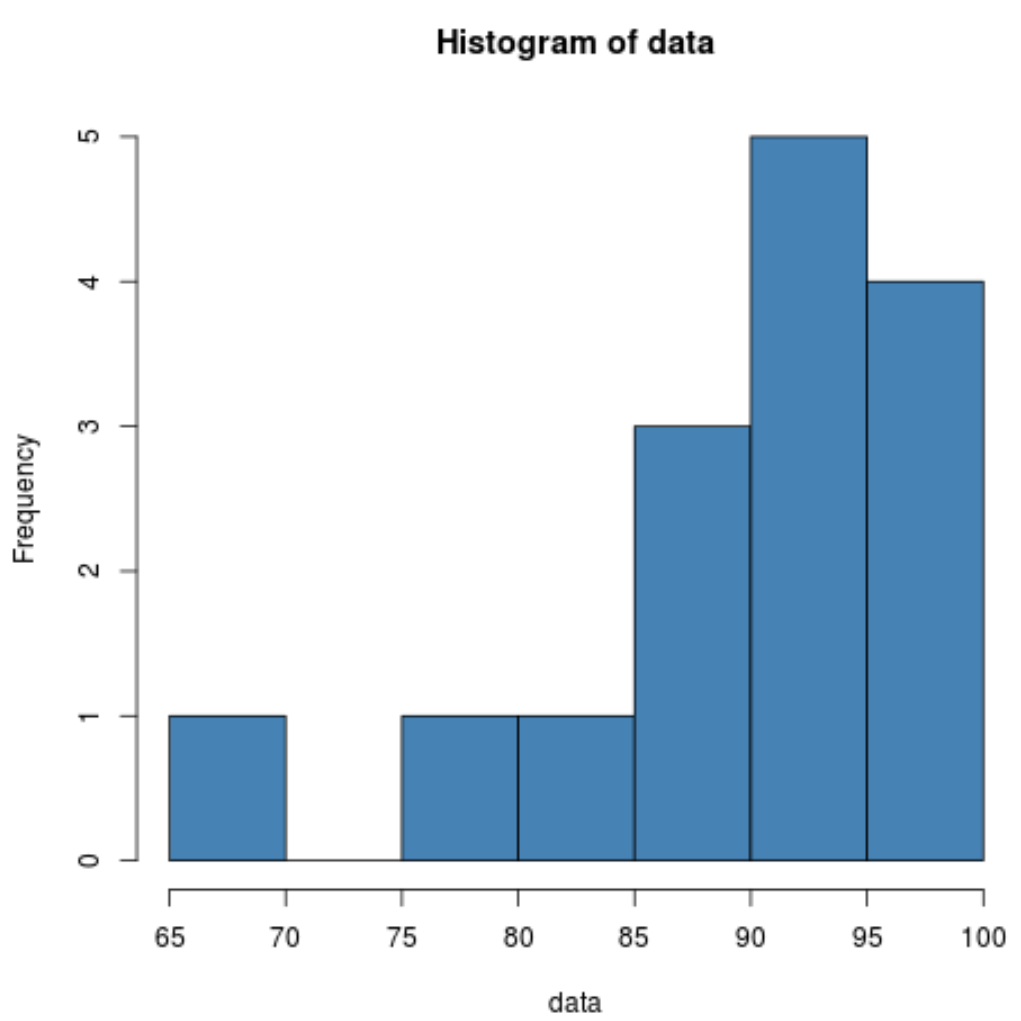
يوضح لنا الرسم البياني أن التوزيع يبدو منحرفًا نحو اليسار. أي أن جزءًا أكبر من القيم يتركز على الجانب الأيمن من التوزيع.

لحساب الانحراف والتفرطح لمجموعة البيانات هذه، يمكننا استخدام الدالتين skewness() و kurtosis() من مكتبة اللحظة في R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

تبين أن الانحراف هو -1.391777 والتفرطح هو 4.177865 .

وبما أن الانحراف سلبي، فهذا يشير إلى أن التوزيع قد ترك منحرفا. وهذا يؤكد ما رأيناه في الرسم البياني.

وبما أن التفرطح أكبر من 3، فهذا يشير إلى أن التوزيع يحتوي على قيم أكثر في الذيول مقارنة بالتوزيع الطبيعي.

توفر مكتبة اللحظات أيضًا وظيفة jarque.test() ، التي تقوم بإجراء اختبار مدى ملاءمة يحدد ما إذا كانت بيانات العينة تظهر انحرافًا وتفرطحًا يتوافقان مع التوزيع الطبيعي أم لا. الفرضيات الصفرية والبديلة لهذا الاختبار هي كما يلي:

الفرضية الصفرية : تحتوي مجموعة البيانات على انحراف وتفرطح يتوافق مع التوزيع الطبيعي.

الفرضية البديلة : تحتوي مجموعة البيانات على انحراف وتفرطح لا يتوافق مع التوزيع الطبيعي.

يوضح الكود التالي كيفية إجراء هذا الاختبار:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

وتبين أن القيمة p للاختبار هي 0.05756 . وبما أن هذه القيمة لا تقل عن α = 0.05، فإننا نفشل في رفض فرضية العدم. ليس لدينا أدلة كافية لنقول أن مجموعة البيانات هذه بها انحراف وتفرطح يختلفان عن التوزيع الطبيعي.

يمكنك العثور على وثائق مكتبة اللحظات الكاملة هنا .

المكافأة: حاسبة الانحراف والتفرطح

يمكنك أيضًا حساب الانحراف لمجموعة بيانات معينة باستخدام حاسبة الانحراف والتفرطح الإحصائية ، التي تحسب الانحراف والتفرطح تلقائيًا لمجموعة بيانات معينة.